機會約束規劃
出自 MBA智库百科(https://wiki.mbalib.com/)
機會約束規劃(Chance Constrained Programming)
目錄 |
隨機規劃的三個分支是期望值模型、機會約束規劃和相關機會規劃。其中機會約束規劃是由查納斯(A.Charnes)和庫伯(W.W.Cooper)於1959年提出的,是在一定的概率意義下達到最優的理論。它是一種隨機規劃方法,針對約束條件中含有隨機變數,並且必須在觀測到隨機變數的實現之前做出決策的問題。
機會約束規劃考慮到所做決策在不利的情況發生時可能不滿足約束條件,而採用一種原則:即允許所做決策在一定程度上不滿足約束條件,但該決策使約束條件成立的概率不小於某一個足夠小的置信水平。對一些特殊情況,機會約束規劃問題可以轉化為等價的確定性數學規劃問題,但對於較複雜的機會約束規劃問題,則要利用基於隨機模擬的遺傳演算法來求解一般機會約束規劃問題以及機會約束多目標規劃和機會約束目標規劃問題。
機會約束規劃主要特點是約束條件中含有隨機參數,其一般形式如下:
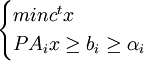
其中Ai = (aij)sm,bi為s維向量,且Ai與bi部分或全部為隨機變數,c ∈Rm為繫數,x∈Rm為決策向量,0 < αi < 1。
機會約束規劃的解法大致有兩種。其一,將機會約束規劃轉化為確定性規劃,然後用確定性規劃的理論去解決;其二,通過隨機模擬技術處理機會約束條件,並利用遺傳演算法的優勝劣汰,得到機會約束規劃的目標函數最優值和決策變數最優解集。
機會約束規劃的目標函數最優值及決策變數的最優解集與模型中的隨機繫數有關,因而具有隨機性。從數理統計的角度看,對這種隨機的目標函數最優值以及決策變數的最優解集可以作出某種置信水平的區間估計。衡量區間估計的精度的一個重要指標是估計區間的長度,估計區間長度越小,估計精度就越大;反之,估計區間長度越大,估計精度就越小。
機會約束規劃模型的案例分析[1]
- 案例:風險管理的機會約束規劃模型
將風險發生概率Pf、風險後果概率Cf以及風險管理的費用作為隨機因素處理,卜面給出這三個隨機因素的詳細描述:
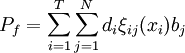 (1)
(1)
這裡d_i是風險岡素i對風險發生的權重.bj是風險等級j的等級值.
ξij(xi)是為風險岡素i選擇措施xi時風險發生處於等級j的概率.管理者在對風險控制措施作山選擇之前,需要邀請數位專家對ξij(xi)進行預測,從而得劍一個最優的決策.然而,風險岡素的狀態是不確定的,並且不同專家的預測結果也不盡相同,從這個角度來說,ξij(xi)不是一個確定的值。於是,把ξij(xi)作為隨機變數來描述,由分佈函數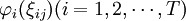 來近似專家們的預測.Xi是為風險因素f選擇的控制措施,
來近似專家們的預測.Xi是為風險因素f選擇的控制措施,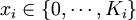
相似的,
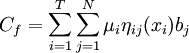 (2)
(2)
這裡μi是風險後果因素i的權重;ηij(xi)是為風險因素i選擇措施x_i時風險後果處於等級j的概率,它是一個隨機變數,其分佈函數近似為φi(ηij)。
風險管理的總費用表示為
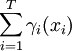 (3)
(3)
γi(xi))是風險因素i選擇其措施xi的費用,為隨機變數,與其對應的分佈函數為Φi(γi),i=1,2,…,T。用於風險管理的總費用不能超過預算資金Cmax:
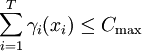 (4)
(4)
綜上所述,風險管理的機會約束規劃模型為
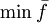 (5)
(5)
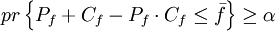 (6)
(6)
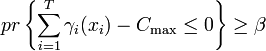 (7)。
(7)。
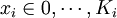 (8)
(8)
其中pr{·}表示{·}中的事件成立的概率.對於模型中的第1個約束(式(5)),多個目標值都可以滿足它.在本問題中,要找出最小的,作為模型的目標值,即:
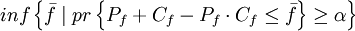 (9)
(9)
式(9)是隨機變數ξij和ηij的一個α悲觀集,目標值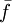 是滿足該約束的值中最小的一個。可見,管理者對待風險的態度是十分謹慎的,即管理者是厭惡風險的。
是滿足該約束的值中最小的一個。可見,管理者對待風險的態度是十分謹慎的,即管理者是厭惡風險的。
由於模型是一個帶有隨機變數的優化問題,考慮用蒙特卡洛模擬嵌入粒子群演算法對問題進行求解。
- ↑ 盧福強 黃敏 王興偉.虛擬企業風險管理的機會約束規劃模型及演算法.信息與控制.2009年8月第38捲第4期







