替代效應
出自 MBA智库百科(https://wiki.mbalib.com/)
替代效應(Substitution Effect)
目錄[隱藏] |
替代效應概述[1]
一種商品的名義價格(nominal price)發生變化後,將同時對商品的需求量發生兩種影響:一種是因該種商品名義價格變化,而導致的消費者所購買的商品組合中,該商品與其他商品之間的替代,稱為替代效應(substitution effect)。另一種是在名義收入不變的條件下,因一種商品名義價格變化,導致消費者實際收入變化,而導致的消費者所購商品總量的變化,稱為收入效應(income effect)。
圖-1描述了當其他商品(用y表示)價格不變,x商品降價(預算線斜率改變)後的總效應、替代效應和收入效應。
替代效應是指當工資率上漲時,單位時間所獲得的收入增加,勞動者為獲得更多的收入,寧願犧牲閑暇,增加勞動量以多獲得工資收入。收入效應是指隨著工資率的提高,勞動者可以用減少的工作時間獲得同樣的收入,因此當工資率提高時勞動者的供給反而減少。這兩種效應的相對強弱就決定於勞動供給曲線的特殊形狀,當替代效應大於收入效應時提高工資率會使勞動供給量增加,供給曲線上各點切線的斜率為正,向右上方延伸,當收入效應大於替代效應時,提高工資率反而會使勞動供給減少,所以勞動的供給曲線向後彎曲。
替代效應是當價格的變化使得消費者沿著無差異曲線移動到不同的邊際替代率的某一點時所產生的消費變化。
總效應與收入效應、替代效應之間的關係[1]
x商品降價前,x與y兩商品的價格比率由預算線aj表示,消費者達到效用最大化的均衡點在E0點,在該點預算線aj與無差異曲線U1相切。與該切點相對應的x商品的購買量為q0,x商品降價後,預算線由aj變為aj2這條新的預算線表示x、y兩商品的新的價格比率。新預算線與較高的無差異曲線相切,切點為E2點。E2點是降價後消費者達到效用最大化的均衡點。與該點相對應的x商品的購買量為q2。可見,x商品降價後,其需求量由q0變到q2。
根據這一變化,我們可以用不同條件下該商品需求量的變動,來定義總效應、替代效應與收入效應。
總效應:某商品價格變化的總效應是,當消費者從一個均衡點移動到另一個均衡點時,該商品需求量的總變動。在圖-1中,總效應是q2 − q0。
替代效應:替代效應是在商品的相對價格發生變化,而消費者的實際收入不變情況下商品需求量的變化。在圖-1中,替代效應是q1 − q0。
這裡所說的實際收入不變是指消費者維持在原來的效用水平上,但又要用新的價格比率(由預算線aj2的斜率表示)來度量這一不變的效用水平。降價後,為了使消費者效用水平不變,就必須畫一條與預算線aj2,相平行、但是與原無差異曲線U1相切的預算線,在圖-1中,這條預算線是a1j1。a1j1與無差異曲線相切於E1點。與E1點相對應的x商品的購買量是q1。
收入效應:一種商品價格變化的收入效應是指在其他所有商品的名義價格與名義收入不變的情況下,完全由實際收入而引起的商品需求量的變化。在圖-1中,收入效應是q2 − q1。這純粹是由實際收入的變化引起的。
總效應與收入效應、替代效應之間的關係是,總效應等於收入效應加替代效應。就圖-1而言q2 − q1 = (q1 − q0) + (q2 − q0)。
圖-1所反映的是正常品的情況。由於正常品的需求收入彈性大於零,因而正常品的收入效應是需求量與實際收入同方向變化,即實際收入增加,需求量增加;實際收入減少,需求量也減少。
正常品的收入效應強化了替代效應。一種商品的價格降低,消費者會用該商品去替代其他商品,從而使得該商品需求量增加。但商品價格的下降同時也意味著實際收入的提高,對正常品而言,這就意味著需求量的增加。由於收入效應與替代效應在同一方向上起作用。所以,對正常品而言,其需求量與價格反方向變化。
正常品收入效應與替代效應同方向變化的情況由圖-1中的箭頭來表示。
劣等品的收入效應與替代效應[1]
劣等品的情況不同於正常品。由於劣等品的需求收入彈性小於零,因而劣等品的收入效應是需求量與實際收入反方向變化,即實際收入增加,需求量減少;實際收入減少,需求量增加。
若某種商品是劣等商品,其價格變化後,收入效應與替代效應在相反的方向起作用。因此,收入效應使得替代效應減弱。圖-2描述了劣等品收入效應與替代效應的情況。
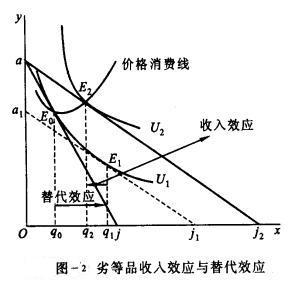
圖-2中,總效應是q2 − q0;替代效應是q1 − q0;收入效應等於總效應減替代效應,即
收入效應=(q2 − q0) − (q1 − q0) = q2 − q1
圖-2表明q2小於q1,所以收入效應是負的值,說明收入替代效應在相反的方向起作用價格消費線(如圖-2中的箭頭方向所示),收入效應小於零的結果是使得總效應小於替代效應。
儘管收入效應與替代效應在相反的方向起作用,由於在絕對值上替代效應大於收入效應,所以價格下降總的結果是該商品的需求量增加了。價格消費線仍向右方傾斜。由此而導出的需求曲線也是向右下方傾斜的。因此,即使是劣等品,一般情況下也遵循需求法則,只不過需求曲線的價格彈性比較小。
吉芬商品的收入效應與替代效應[1]
若收入效應與替代效應在相反的方向起作用,而且從絕對值上講收入效應大於替代效應,則該商品是一種特殊的劣等品,稱為吉芬商品。
圖-3顯示了吉芬商品的收入效應與替代效應。圖中,總效應為q2 − q0,由於q2小於q0,所以x商品降價後的總效應是負的值;替代效應為q1 − q0;收入效應為(q2 − q0) − (q1 − q0) = q2 − q1
由於q2小於q1,所以收入效應為負值。又由於在絕對值上收入效應大於替代效應,所以,商品降價後總效應是負的值,即需求量下降了。價格消費線向左方而不是向右方傾斜。
可以就商品降價後所產生的各種效應的變化歸結如下。不管商品是正常品,還是一般的劣等品,或是吉芬商品,商品降價後的替代效應總是正值,這表明,只要該商品降價,消費者就會用讀商品去替代其他商品。對於正常品而言,收入效應與替代效應在同一方向上起作用,表明在商品降價後,收入效應與替代效應都是正值。總效應必然大於零,表示商品降價後需求量增加。對於一般的劣等品而言,雖然收入效應與替代效應在相反的方向起作用,但是在絕對值上替代效應仍然大於收入效應。商品降價後正值的替代效應在絕對值上大於負值的收入效應,總效應仍然大於零,表示商品降價後枯求量也是增加的。只有那些特殊劣等品即吉芬商品,在商品降價後,不僅收入效應與替代效應在相反的方向起作用,而且在絕對值上收入效應大於替代效應,導致商品降價後總效應小於零。這表明商品降價後,需求量不僅沒有增加,反而減少了。
應該註意的是,不要混淆吉芬商品與劣等品。劣等品是從需求與收人的關係定義的,即需求的收入彈性小於零的商品是劣等品。而吉芬商品是從需求量與價格的關係定義的,即需求量與價格同方向變化的商品是吉芬商品,只不過在討論吉芬商品時用到了收入效應的概念。
希克斯替代效應與斯勒茨基替代效應[1]
希克斯替代效應(Hicksian substitution effect)與斯勒茨基替代效應(Slutsky substitution effect)是分別以兩位經濟學家約翰·希克斯(John Richard Hicks,1904年4月8日—1989年5月20日)與斯勒茨基(E. Slustsky)的名字命名的。
如前所述,替代效應是指商品相對價格變化後,而令消費者實際收入不變情況下所引起的商品需求量的變化。希克斯替代效應與斯勒茨基替代效應的差別,在於他們對什麼是消費者實際收入不變所下的不同定義。在希克斯替代效應中,實際收入不變是指使消費者在價格變化前後保持在同一條無差異曲線上;而在斯勒茨基替代效應中,實際收入不變是指消費者在價格變化後能夠買到價格變動以前的商品組合。
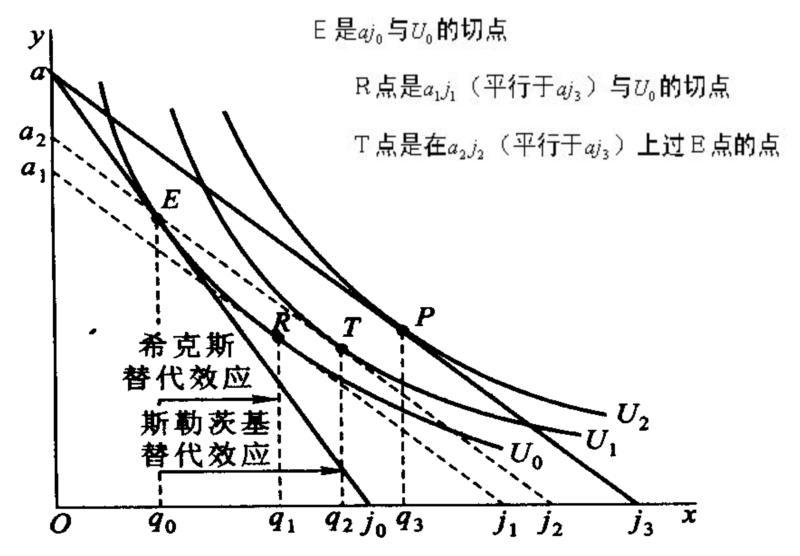
圖-4 希克斯替代效應與斯勒茨基替代效應
圖-1到圖-3中所討論的替代效應都屬於希克斯替代效應。我們利用圖-4討論斯勒茨基替代效應,並與希克斯替代效應進行比較。
圖-4中的橫坐標表示某種特定的商品,縱坐標y表示除了x商品以外的所有其他商品。我們討論y商品價格不變,x商品價格下降以後的斯勒茨基替代效應。x商品降價前,預算線為aj0,aj0與無差異曲線U0相切於E點,E點是消費者效用最大化的均衡點。在E點,x商品的購買量為q0。x商品降價後,預算線變為aj3,消費者效用最大化的均衡點為P點。
假定我們想在x商品降價後維持消費者的實際收入不變。按照希克斯替代效應中所定義的實際收入,應該使消費者在新的價格比率下回到x商品降價前的無差異曲線上,通過畫一條與aj3相平行、並與原無差異曲線U0相切的預算線可以保證這種意義上的實際收入不變。圖-4中a1j1線便是我們所需要的預算線,a1j1與U0相切於R點,與R點相對應的x商品的購買量為q1,q1 − q0便是希克斯替代效應。
按照斯勒茨基替代效應中所定義的實際收入,若想在x商品降價後維持消費者的實際收入不變,應該使消費者在新的價格比率下能夠購買他在降價前所能購買的商品數量,即能夠購買圖-4中E點所表示的商品數量。通過畫一條與預算線aj3相平行、並且過E點的預算線可以保證這種意義上的實際收入不變。圖-4中的a2j2線便是我們所需要的預算線。a2j2和一條高於無差異曲線U0、低於無差異曲線U2的無差異曲線U1相切,切點為T。與T點相對應的x商品的購買量為q2。q2 − q0為斯勒茨基替代效應。由於q2大於q1,所以斯勒茨基替代效應大於希克斯替代效應。
我們也可以用代數式討論斯勒茨基替代效應。令消費者的貨幣收人為M,降價前x商品的價格為Px,降價後為 ,降價前對x商品的需求函數為
,降價前對x商品的需求函數為
x = x(Px,M)(3.35)
降價後對x商品的需求函數為
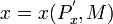 (3.36)
(3.36)
x商品降價後對x商品需求的總效應為
 (3.37)
(3.37)
分為兩部分,收入效應Δxm與替代效應Δxs,
Δx = Δxm + Δxs(3.38)
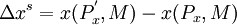 (3.39)
(3.39)
其中是在x降價為後,為了維持降價前的購買數量組合而調整後的收入。
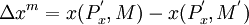 (3.40)
(3.40)
因此,
![\Delta x=\Delta x^m+\Delta x^s=\left[x(P^'_x,M^')-x(P_x,M)\right]+\left[x(P^'_x,M)-x(P^'_x,M^')\right]](/w/images/math/6/c/a/6cacdaa07158bb77ac2a9b9676bdf751.png) (3.41)
(3.41)
(3.41)式與(3.37)式雖然是恆等式,但(3.41)式是以代數形式將商品價格變化後的收入效應與替代效應明確地表示出來。
由Δx = δxm + Δx5,我們知道,x商品價格變動後總效應Δx符號取正的值還是取負的值,取決於x商品是工常品、一般劣等品、還是吉芬商品。我們分x商品降價與提價兩種情況進行討論。
若x商品降價,Δxs總是取正的值。對於正常品而言,Δxm也取正的值,因此總效應Δx的值是正的;對於一般劣等品而言,降價後,Δxm取負的值,但從絕對值講,Δxm小於Δxs,因此總效應Δx的值仍然是正的;對於吉芬商品而言,降價後,Δxm取負的值,而且從絕對值講,Δxm大於Δxs,因此總效應Δx的值是負的。
若x商品提價,Δxs總是取負的值。對於正常品而言,Δxm也取負的值,因此總效應Δx的值是負的;對於一般劣等品而言,提價後,Δxm取正的值,但從絕對值講,小於Δxs,因此總效應Δx的值仍然是負的;對於吉芬商品而言,提價後,取正的值,而且從絕對值講,Δxm大於Δx5,因此總效應Δx的值是正的。
在x商品價格變動後,要維持消費者的實際收入不變,即要使消費者能夠買得起x商品價格變動前他所購買的各種商品組合量,收人應該變動多大的數量?也就是說,當x商品的價格變動為ΔPx時,ΔM是多少?可以證明
 (3.42)
(3.42)
(3.42)式的推導過程如下。假定消費者消費x、y(y代表除x商品以外的所有其他商品)兩種商品。x商品價格變動前,消費者的預算線為
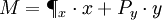 (3.43)
(3.43)
x商品價格由Px變為 後,要便消費者仍能購買他在價格變動前所能購買的x、y數量,預算線應該是
後,要便消費者仍能購買他在價格變動前所能購買的x、y數量,預算線應該是
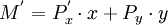 (3.44)
(3.44)
我們已經指出,M'是x商品價格變動後,為了維持價格變動前的購買數量組合而調整後的收入。由(3.43)式與(3.44)式我們得到
這便是(3.42)式。
斯勒茨基替代效應的概念可以作為政府制定政策的參考。例如,政府決定在豬肉漲價後對消費者進行價格補貼。假定消費者每月消費2.5千克肉,原價12元錢1千克肉。現價格提高到14元錢1千克,要使消費者在肉漲價後仍能買得起2.5千克肉,給消費者的補貼應該是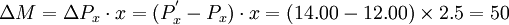 (元)。
(元)。
商品價格變化所引起的替代效應與收入效應[2]
商品類別 替代效應與價格的關係 收入效應與價格的關係 總效應與價格的關係 需求曲線的形狀 正常品 反方向變化 反方向變化 反方向變化 向右下方傾斜 低檔品 反方向變化 同方向變化 反方向變化 向右下方傾斜 吉芬商品 反方向變化 同方向變化 同方向變化 向右上方傾斜
替代效應舉例分析[3]
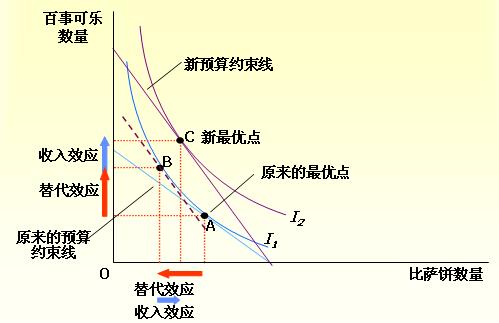
- 價格變動:替代效應
價格變動首先使消費者沿著同一條無差異曲線從一點移動到另一點。
在圖上看就是從A點移動到B點。
- 價格變動:收入效應
在同一條無差異曲線上從一點移動到另一點以後,消費者將移動到另一條無差異曲線上。
從圖上看就是從B點移動到C點。
表1. 當百事可樂價格下降時的收入與替代效應
物品 收入效應 替代效應 總效應 百事可樂 消費者更富了,因此他購買了更多的百事可樂。 百事可樂相對便宜了,因此消費者購買了更多的百事可樂。 收入與替代效應同方向發生作用,因此消費者購買更多的百事可樂。 比薩餅 消費者更富了,因此他購買了更多的比薩餅。 比薩餅相對貴了,因此消費者購買的比薩餅少了。 收入與替代效應反方向發生作用,因此對比薩餅的總效應難以確定。
本条目由以下用户参与贡献
18°@鷺島,Kane0135,Angle Roh,Dan,Zfj3000,Cabbage,Yixi,Xiaoqingyun,王欣,东风,徐梦良,黄金通,Lin,Yogi XMU FINANCE,186****4868,LuyinT,陈cc.評論(共26條)
一種物品價格下降,替代效應總會引起該物品的需求量增加
初入經濟這一塊 還不是很懂.. 和英文教材差異太大了
我也覺得,期末複習看老師ppt很難理解 來這看了以後更迷惑了
感謝,上課沒聽光看圖不懂現在終於懂了
多謝,上課的時候沒聽懂,看書上也沒有講的很詳細,在這裡終於看懂了,謝謝!
圖中*

 无广告阅读
无广告阅读  免验证复制
免验证复制  微信支付
微信支付  支付宝
支付宝  PayPal
PayPal 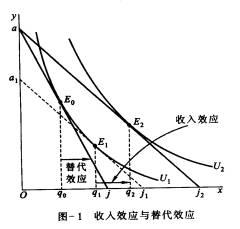












錯誤連篇