總供給函數
出自 MBA智库百科(https://wiki.mbalib.com/)
總供給函數(Aggregate supply function)
目錄 |
總供給(Aggregate supply)是經濟社會的總產量(或總產出),它描述了經濟社會的基本資源用於生產時可能有的產量。一般而言,總供給主要是由生產性投入(最重要的是勞動與資本)的數量和這些投入組合的效率(即社會的技術)的決定的。
總供給函數(Aggregate supply function)是指總供給(或總產出)和價格水平之間的關係。在以價格為縱坐標,總產出(或總收入)為橫坐標的坐標系中,總供給函數的幾何表示為總供給曲線。以y表示經濟中的總產出,P表示價格總水平,則總供給函數AS可以表示為:y = AS(P)
總供給函數的一般形式[1]
假設:
(1)該國所有企業和家庭都生產同樣的產品,且具有同一的生產函數。
(3)家庭和企業的供給決策基於當期的價格和工資。
(4)家庭或企業的供給函數直接被視為總供給函數。
數學推導:
設典型企業生產函數為:Q = Q(K,L,τ)
且
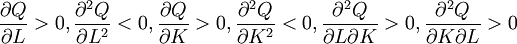
=>企業 的短期生產函數 : Q=Q(L)
典型企業對勞動需求的決策原則:
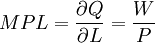 (實際工資)
(實際工資)
證明:
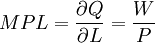
=>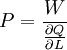
=>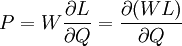
=>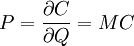 即完全競爭下廠商利潤最大化原則
即完全競爭下廠商利潤最大化原則
結論1:企業勞動需求函數為:LD = LD(W / P,K,τ)
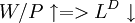
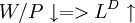
結論2: 總供給函數(即單個企業的供給函數)為:
Q5 = Q5[LD(W / P,K,τ),K,τ]
結論3: 短期總供給函數:Q5 = Q5(W / P)
且
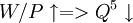

總供給函數的幾何表達[2]
在以價格水平為縱坐標、總產量為橫坐標的坐標系中,總供給函數的幾何表達即為總供給曲線。按照貨幣工資(W)和價格水平(P)進行調整所要求的時間長短,巨集觀經濟學將總產出與價格水平之間的關係分為三種:古典總供給曲線、凱恩斯總供給曲線和常規總供給曲線。下麵分別進行討論。
- (一)古典總供給曲線
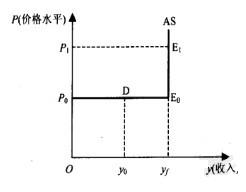
按照西方古典學派的說法,在長期,價格和貨幣工資具有伸縮性,因此經濟的就業水平處在充分就業的狀態上。在不同的價格水平下,當勞動市場存在超額勞動供給時,貨幣工資就會下降,價格水平也會上升。反之,當勞動市場存在超額勞動需求時,貨幣工資就會提高,價格水平也會下降。這些變化最後會使實際工資調整到使勞動市場達到均衡的水平。也就是說,在長期,經濟的就業水平或產量並不隨著價格水平的變化而變化,而始終處在充分就業的狀態上,經濟的產量水平也將位於潛在產量或充分就業的水平上,不受價格變動的影響。因此,古典學派認為,總供給曲線是一條位於經濟的潛在產量或充分就業水平上的垂直線。圖1中的垂直線即為古典總供給曲線。
古典供給曲線之所以是垂直線形狀,一般有兩個理由。第一,古典學派假設貨幣工資(W)和價格水平(P)可以迅速或立即自行調節,使得實際工資(W/P)總是處於充分就業所應有的水平,從而,產量或國民收入也總是處於充分就業的水平,不受價格的影響。根據這一理由,古典總供給曲線並不意味著時期的長短。換言之,只要存在緲和P迅速或立即調整的假設,古典總供給曲線也是一個短期總供給曲線。第二,古典學派一般研究經濟事物的長期狀態,而在長期中,即使不使用W和P能夠迅速或立即調整的假設,貨幣工資和價格水平被認為是具有充分的時間來進行調整,使得實際工資(W/P)處於充分就業應有的水平,從而,總供給曲線也是一條垂直線。以此而論,古典總供給曲線又代表長期總供給曲線。
究竟垂直的總供給曲線代表的是短期還是長期的狀態?在目前的西方經濟學文獻中,由於上述兩個理由均被使用,所以它究竟代表短期還是長期取決於上述兩個理由的使用。在使用第一個理由時,它被認為是短期總供給曲線的一種極端情況,即W和P能夠立即自行調節。在使用第二個理由時,它被認為是長期總供給曲線。為了避免混淆,本書採用了大多數西方文獻的辦法,把垂直的總供給曲線稱為古典總供給曲線,而除了在例外的情況下,一般把它當作為短期總供給曲線的極端狀態。如圖1中的垂直線即為古典總供給曲線。
古典總供給曲線的政策含義可以用圖2表示。
在圖2中,總需求曲線AD0與古典總供給曲線yf垂直線相交於E0點;此時的價格水平為P0,就業量是充分就業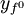 處於E0的狀態下,國家即使通過增加需求的政策來使AD0向右移動到AD1的位置,其與yf垂直線的新交點為E1。在E1點,價格水平為P1,可是產量仍然是yf。也就是說,增加需求的政策並不改變產量,而只能造成物價上漲,甚至通貨膨脹。
處於E0的狀態下,國家即使通過增加需求的政策來使AD0向右移動到AD1的位置,其與yf垂直線的新交點為E1。在E1點,價格水平為P1,可是產量仍然是yf。也就是說,增加需求的政策並不改變產量,而只能造成物價上漲,甚至通貨膨脹。
- (二)凱恩斯總供給曲線
凱恩斯在《就業、利息和貨幣通論》中提出了貨幣工資具有“剛性”的假設,即假設由於種種原因,貨幣工資不會輕易變動。這個假設的背景是20世紀30年代初期整個西方世界都處於嚴重的大蕭條時期,經濟社會存在著大量的失業人口和生產能力。貨幣工資的剛性包括兩層含義:一是完全不能調整:二是在時間很短的情況下,W和P沒有足夠的時間進行調整。
在這種狀態下,當產量(從而國民收入)增加時,價格和貨幣工資均不會發生變化。因此,凱恩斯總供給曲線被認為是一條水平線,如圖3所示。
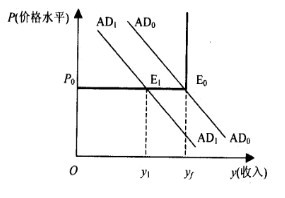
凱恩斯總供給曲線的政策含義是:只要國民收入或產量處在小於充分就業的水平,那麼國家就可以使用增加需求的政策來達到充分就業狀態。如圖4所示,總需要曲線AP1與總供給曲線相交於E1,此時價格為P0,產品量為y1,未達到充分就業水平。增加總需求,總需求曲線右移,由AD1移至AD0,與總供給曲線相交於E0,此時價格仍為P0,但產量增加至yf,即達到充分就業狀態的產量。
- (三)常規總供給曲線
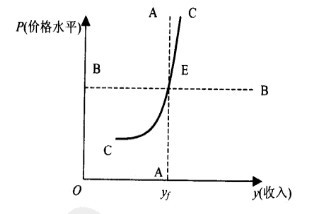
古典總供給曲線和凱恩斯總供給曲線都是極端情況,在通常情況下,常規總供給曲線位於兩個極端之間。為了方便教學,我們通常用線形形式進行表達,而實際上常規總供給曲線卻是非線形的,如圖5所示。
該圖的CC線即為非線性的常規總供給曲線。圖中,左下方的C點代表較為嚴重的蕭條狀態;由於這種狀態存在著大量的失業和閑置的生產能力,所以當產量或國民收入(y)增加時,P會稍有上升,但上升的速度不會很快,從而CC的斜率相對平緩。由左方的C點沿著CC向右方行進,產量和國民收入逐漸上升,隨著經濟的好轉,P的上升越來越快,從而CC的斜率日益陡峭,一直到代表充分就業的E點。這時,由於充分就業並不意味著整個社會的全部資源和有勞動能力的人口均已就業,所以仍然存在著難以利用的資源和能力較差的勞動者,因此,在E點之後,如果產量還要增加,那麼,P的上升還要加快,從而CC的斜率也越來越大。總之,在位於E點左方的CE線段,離開E點的距離越遠,曲線的斜率越低,而在處於E點右方的EC線段,離開E點的距離越大,曲線的斜率越高。西方學者認為,這種形狀的總供給曲線可以代表西方經濟的常規狀態。










這幾個結論在詳細一點就好了