哈夫模型
出自 MBA智库百科(https://wiki.mbalib.com/)
哈夫模型(huff's model,時間面積商圈界限模型)
目錄 |
在哈裡斯的市場潛能模型的基礎上,美國加利福尼亞大學的經濟學者戴維·哈夫(D.L.Huff)教授於1963年提出了關於預測城市區域內商圈規模的模型--哈夫概率模型 。
哈夫概率模型基本法則依然是引用萬有引力原理。它提出了購物場所各種條件對消費者的引力和消費者去購物場所感覺到的各種阻力決定了商圈規模大小的規律。哈夫模型區別於其他模型的不同在於模型中考慮到了各種條件產生的概率情況。
哈夫認為:從事購物行為的消費者對商店的心理認同是影響商店商圈大小的根本原因,商店商圈的大小規模與消費者是否選擇該商店進行購物有關,通常而言,消費者更願意去具有消費吸引力的商店購物,這些有吸引力的商場通常賣場面積大,商品可選擇性強,商品品牌知名度高,促銷活動具有更大的吸引力;而相反,如果前往該店的距離較遠,交通系統不夠通暢,消費者就會比較猶豫,根據這一認識,哈夫提出其關於商店商圈規模大小的論點:
哈夫論點:商店商圈規模大小與購物場所對消費者的吸引力成正比,與消費者去消費場所感覺的時間距離阻力成反比。商店購物場所各種因素的吸引力越大,則該商店的商圈規模也就大;消費者從出發地到該商業場所的時間越長,則該商店商圈的規模也就越小。
哈夫從消費者的立場出發,認為消費者前往某一商業設施發生消費的概率,取決於該商業設施的營業面積、規模實力和時間三個主要要素。商業設施的營業面積大小反映了該商店商品的豐富性,商業設施的規模實力反映了該商店的品牌質量、促銷活動和信譽等,從居住地到該商業設施的時間長短反映了顧客到目的地的方便性。同時,哈夫模型中還考慮到不同地區商業設備、不同性質商品的利用概率,這個模型的公式表現如下:
(μ表示賣場魅力或商店規模對消費者選擇影響的參變數,λ表示需要到賣場的時間對消費者選擇該商店影響的參變數,通常μ = 1,λ = 2
哈夫提出,一個零售商業中心 J 對消費者的吸引力可與這個商場的賣場魅力(主要用賣場面積代替)成正比 (J=1,2, … n) ,與消費者從出發地 I 到該商場 J 的阻力(主要用時間距離來代替)成反比。
利用哈夫模型設定地點 I 的消費者選擇商場 J 的概率 PIJ ,
【PIJ】 = I 地區消費者到 J 商店購物的概率;
【SJ】 = J 商店的賣場吸引力(賣場面積、知名度、促銷活動等)
【TIJ】 = I 地區到 J 商店的距離阻力(交通時間、交通系統等)
【λ 】 = 以經驗為基礎估計的變數;
【n】 = 互相競爭的零售商業中心或商店數
由此可以推導出以下概率公式:
I 地區消費者光顧 J 商店的人數 = I 區消費者光顧 J 商店的概率× I 地區消費者的數量
A 、消費者光顧賣場的概率會因零售店賣場面積而變化,賣場面積同時代表商品的齊全度及用途的多樣化。
B 、消費者會因購物動機而走進零售店賣場。
C 、消費者到某一零售店賣場購物的概率受其他競爭店的影響。競爭店越多,概率越小。
哈夫模型是國外在對零售店商圈規模調查時經常使用的一種計算方法,主要依據賣場引力和距離阻力這兩個要素來進行分析,運用哈夫模型能求出從居住地去特定商業設施的出行概率,預測商業設施的銷售額,商業集聚的集客能力及其表化,從而得知商圈結構及競爭關係會發生怎樣的變化,在調查大型零售店對周邊商業集聚的影響力時也經常使用這一模型。
哈夫概率法則的最大特點是更接近於實際,他將過去以都市為單位的商圈理論具體到以商店街、百貨店、超級市場為單位,綜合考慮人口、距離、零售面積規模等多種因素,將各個商圈地帶間的引力強弱、購物比率發展成為概率模型的理論。
哈夫模型不僅是從經驗推導出來的,而且表達了消費者空間行為理論的抽象化。考慮了所有潛在購物區域或期待的消費者數,這個模型考慮了營業網點的面積,顧客的購物時間,顧客對距離的敏感程度,經統計可得出消費者對不同距離到目標店購物的概率。各零售店可根據自身的情況不同,設立不同的概率標準,選擇在一定概率下的距離來劃定商圈範圍。
在哈夫模型中,通常用到賣場的時間距離作為阻力因素,而用賣場的面積來代替賣場的吸引力,但如果僅用賣場的面積來代替賣場引力,那相同面積的百貨店、超市、商業街就具有相同的魅力,這顯然過於武斷。
哈夫模型通常將商業面積的修正值在運用上不僅必須使用電腦,而且還必須通過市場調查計算出 λ 值,這得花費相當多的時間和費用。同時哈夫的各個修正參數和具體情況不相適應,不同地區的商業情況和消費文化各有不同,這就使得各地區的參數差異較大,難以正確反映實際情況 。
另外,對於各值的計算標準也將直接影響該模型的計算精度。
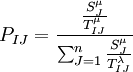








挺好的