博弈
出自 MBA智库百科(https://wiki.mbalib.com/)
博弈（Game）
目錄 |
博弈是指在一定的游戲規則約束下，基於直接相互作用的環境條件，各參與人依靠所掌握的信息，選擇各自策略（行動），以實現利益最大化和風險成本最小化的過程。簡單說就是人與人之間為了謀取利益而競爭。
通俗地講，博弈就是指在游戲中的一種選擇策略的研究，博弈的英文為game，我們一般將它翻譯成“游戲”。而在西方，game的意義不同於漢語中的游戲。在英語中，game即是人們遵循一定規則的活動，進行活動的人的目的是讓自己“贏”。而自己在和對手競賽或游戲的時候怎樣使自己贏呢？這不但要考慮自己的策略，還要考慮其他人的選擇。生活中博弈的案例很多，只要有涉及人群的互動，就有博弈。[1]
比如，一天晚上，你參加一個派對，屋裡有很多人，你玩得很開心。這時候，屋裡突然失火，火勢很大，無法撲滅，此時你想逃生。你的面前有兩個門，左門和右門，你必須在它們之間選擇。但問題是，其他人也要爭搶這兩個門出逃。如果你選擇的門是很多人選擇的，那麼你將因人多擁擠、沖不出去而被燒死；相反，如果你選擇的是較少人選擇的，那麼你將有望逃生。這裡我們不考慮道德因素，你將如何選擇？[1]
- 參與人：參與博弈的決策主體。誰參與了博弈？
- 規則：對博弈作出具體規定的集合。誰在何時行動？他行動時知道什麼？他能選擇什麼樣的行動？
- 結果：對於參與人行動的每一個可能的集合，博弈的結果是什麼？
- 贏利：在可能的每一個結果上，參與者的所得和所失。參與人在每個可能結果上的偏好（即效用函數）是什麼？
博弈模型一般分為合作博弈（cooperative game）和非合作博弈（non-cooperative game），【如圖1.1】。合作博弈是以單個參與者的可能行動集合為基本元素，而非合作博弈是以參與人群的可能聯合行動集合為基本元素（Martin J.Osborne and Ariel Rubinstein，2000，P2），也就是說，在合作博弈中，博弈中所有參與者都獨立行動，不存在有約束力的合作、聯合或聯盟的關係，而在非合作博弈中，在一些參與者之間存在著有約束力的合作、聯合或聯盟的關係，並因為這種關係影響到博弈的結局。合作博弈強調的是團體理性（collective rationality）、效率、公正和公平；非合作博弈強調的是個人理性、個人最優決策，其結果可能是有效率的，也可能是低效率或無效率的（張維迎，1996，P5）。20世紀50年代，合作博弈的研究達到鼎盛期，同時開始出現對非合作博弈的研究，此後，博弈論的研究主流逐步轉向在非合作博弈領域。有些人認為非合作博弈模型比合作博弈更“基本”，但有些人認為兩者不相上下（Martin J.Osborne and Ariel Rubinstein，2000，P2）。
合作博弈，有時也叫做聯盟博弈（coalitional game），一般根據有無轉移支付而分為兩類：可轉移支付聯盟博弈（coalitional game with transferable payoff）和不可轉移支付聯盟博弈（coalitional game with non-transferable payoff）。可轉移支付也叫有旁支付（side payment），可轉移支付聯盟博弈假設博弈中各參與者都用相同的尺度來衡量他們的贏得，且各聯盟的贏得可以按任意方式在聯盟成員中分攤；否則，就是不可轉移支付聯盟博弈。
非合作博弈的分類主要從兩個角度進行劃分。
一是參與者的行動順序。從這個角度博弈可以分為靜態博弈（static game）和動態博弈（dynamic game）。靜態博弈是指參與者同時選擇行動或雖非同時但後行動者並不知前行動者採取了何種行動；動態博弈是指參與者的行動有先後順序且後行動者能夠觀察到先行動者所選擇的行動。
二是參與者掌握的信息水平。從這個角度，博弈可以分為完全信息博弈和不完全信息博弈。完全信息（complete information）指的是每一個參與者對所有其他參與者的特征、戰略空間及支付函數有準確的知識；否則就是不完全信息（incomplete information）。
綜合上述兩種分類方法，可將非合作博弈分成四類。這四類博弈及其對應的均衡概念，大致上反映了20世紀50年代以來非合作博弈理論的主要進展和1994年三位諾貝爾經濟學將得主的主要貢獻，同時也大致表明瞭“納什均衡”及其精煉在博弈論發展中的地位和影響【如表1.1】。
行動順序 信息 | 靜 態 (參與者同時選擇行動或雖非同時但後行動者並不知前行動者採取了何種行動) | 動 態 (參與者的行動有先後順序且後行動者能夠觀察到先行動者所選擇的行動) |
| 完全信息 (每一參與者對所有其他參與者的特征、戰略空間及支付函數有準確的知識) | 完全信息靜態博弈； 納什均衡； John F.Nash(1950,1951) | 完全信息動態博弈； 子博弈完美納什均衡； Reinhard Selten(1965) |
| 不完全信息 (每一參與者對所有其他參與者的特征、戰略空間及支付函數沒有準確的知識) | 不完全信息靜態博弈； 貝葉斯納什均衡 John C.Harsanyi(1967-1968) | 不完全信息動態博弈； 完美貝葉斯納什均衡； Reinhard Selten(1975), D.Kreps and R.Wilson(1982), D.Fudenberg and J.Tirole(1991) |
現代博弈理論根據不同的博弈類型給出了博弈模型的三種基本表達形式：標準式（normal form）表述、擴展式表述（extensive form representation）和特征函數型表述。前兩者主要用於非合作博弈，後者主要用於合作博弈。
1、標準式表述
標準式表述又稱為戰略式表述（strategic form）或矩陣式表述（matrix form）。標準式表述將戰略局勢抽象為三個基本要素：
（a）博弈的參與者集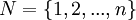
；
（b）每個參與者的戰略集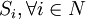
；
（c）每個參與者的支付函數集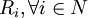 
。
因此，一個標準式表述的博弈可以表示為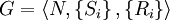 
。標準式表述主要用來表示靜態博弈。標準式博弈也叫做戰略博弈。
2、擴展式表述
擴展式表述在標準式表述的基礎上，擴展了描述博弈局勢的要素，比如參與者的行動順序以及外生事件的概率分佈等，可以描述更複雜的博弈局勢，極大地擴大了博弈理論所能描述的範圍，一般用來表述動態博弈。擴展式表述一般包含六個要素：
（a）博弈的參與者集 ；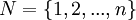
（b）參與者的行動順序（the order of moves）：即什麼參與者在什麼時候行動；
（c）參與者的行動空間（action set）：在每次行動時，參與者有些什麼行動可供選擇；
（d）參與者的信息集（information set）：每次行動時，參與者知道些什麼；
（e）參與者的支付函數：在行動結束時，每個局中人得到什麼；
（f）外生事件（即“自然”的選擇）的概率分佈。
3、特征函數型表述
特征函數型表述主要用來表述聯盟博弈或合作博弈。令參與者集合為N，則稱N的任意子集S為聯盟（coalition），所有聯盟的全體記為 Ψ(N)。可轉移支付聯盟博弈包括兩個要素：
（a）有限的參與者集 ；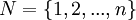
（b）將N的每個非空子集S（即一聯盟）與某個實數v(S)相聯繫的一個特征函數v。
因此，可轉移支付聯盟博弈可記為（N，v）。其中特征函數v是指定義在Ψ(N)上的一個實函數，其中v(S)表示聯盟S通過協調其成員的策略所能保證得到的最大贏得。
不可轉移支付聯盟博弈包括四個要素：
（a）有限的參與者集 ；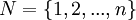
（b）結果集X；
（c）將N的每個非空子集S（即一聯盟）賦一個集合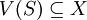
的特征函數V；
（d）對每個參與者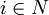
有一個X上的支付函數
。
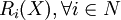因此，不可轉移支付聯盟博弈可記為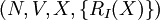
。
博弈的三種表述形式之差別，主要在於描述信息的多寡。擴展型表述形式包括的信息最多，如果去掉其中參與者行動順序和信息結構等信息，可以簡化出標準型表述形式。在標準型表述形式的基礎上，如果引入有約束力的義務且可強制執行的假設，省略掉戰略集，則可進一步簡化為特征函數型表述形式。三種表述形式的可轉化性，表明非合作博弈與合作博弈之間是可轉化的。
好的