決策樹
出自 MBA智库百科(https://wiki.mbalib.com/)
決策樹法(Decision Tree)、決策樹分析法
目錄 |
決策樹,是一種通過圖示羅列解題的有關步驟以及各步驟發生的條件與結果的一種方法。決策樹不僅可以幫助人們理解問題,還可以幫助人們解決問題。
決策樹一般是自上而下的來生成的。每個決策或事件(即自然狀態)都可能引出兩個或多個事件,導致不同的結果,把這種決策分支畫成圖形很像一棵樹的枝幹,故稱決策樹。
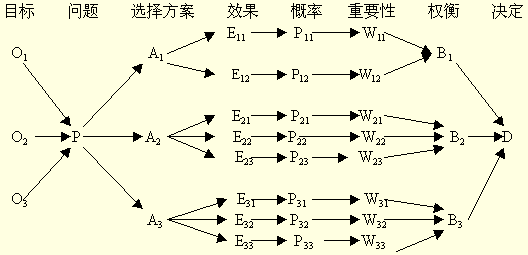
決策樹將決策過程各個階段之間的結構繪製成一張箭線圖,我們可以用下圖來表示。
選擇分割的方法有好幾種,但是目的都是一致的:對目標類嘗試進行最佳的分割。 從決策樹的根到葉子節點都有一條路徑,這條路徑就是一條“規則”。 決策樹可以是二叉的,也可以是多叉的。
決策樹的構成要素[1]
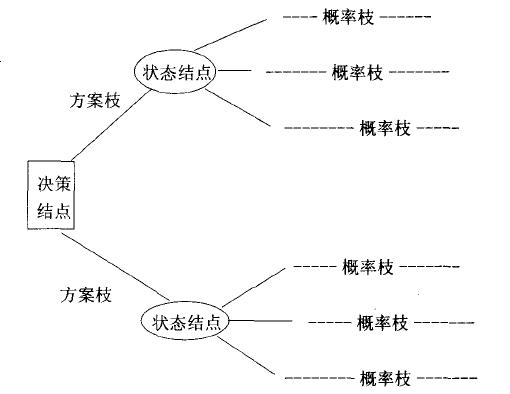
決策樹的構成有四個要素:(1)決策結點;(2)方案枝;(3)狀態結點;(4)概率枝。如圖所示:
決策樹一般由方塊結點、圓形結點、方案枝、概率枝等組成,方塊結點稱為決策結點,由結點引出若幹條細支,每條細支代表一個方案,稱為方案枝;圓形結點稱為狀態結點,由狀態結點引出若幹條細支,表示不同的自然狀態,稱為概率枝。每條概率枝代表一種自然狀態。在每條細枝上標明客觀狀態的內容和其出現概率。在概率枝的最末稍標明該方案在該自然狀態下所達到的結果(收益值或損失值)。這樣樹形圖由左向右,由簡到繁展開,組成一個樹狀網路圖。
繪製方法
1.先畫一個方框作為出發點,這個方框又稱為決策點
2.從決策點向右引出若幹根直線或折線,每根直線或折線代表一個方案,這些直線或折線稱為方案枝
3.每個方案枝的末端畫個圓圈,這個圓圈稱為概率分叉點,也稱為自然狀態點
4.從自然狀態點引出若幹根直線或折線代表各自然狀態的分枝,這些直線或折線稱為概率分枝
5.在概率分枝的末梢標明各自然狀態的損益值
決策樹的分析最佳方案過程就是比較各方案的損益值,哪個方案的期望值最大則該方案為最佳方案
優點:
1) 可以生成可以理解的規則;
2) 計算量相對來說不是很大;
3) 可以處理連續和種類欄位;
4) 決策樹可以清晰的顯示哪些欄位比較重要。
缺點:
1) 對連續性的欄位比較難預測;
2) 對有時間順序的數據,需要很多預處理的工作;
3) 當類別太多時,錯誤可能就會增加的比較快;
4) 一般的演算法分類的時候,只是根據一個欄位來分類。
西蒙說:管理就是決策。從以上介紹可以看出決策樹法具有許多優點:條理清晰,程式嚴謹,定量、定性分析相結合,方法簡單,易於掌握,應用性強,適用範圍廣等。人們逐漸認識到,在投資方案比較選擇時考慮時間因素,建立時間可比原則和條件的重要性。當今的社會經濟活動中,競爭日趨激烈,現代企業的經營方向面臨著許多可供選擇的方案,如何用最少的資源,贏得最大的利潤以及最大限度地降低企業的經營風險,是企業決策者經常面對的決策問題,決策樹法能簡單明瞭地幫助企業決策層分析企業的經營風險和經營方向。必然地,隨著經濟的不斷發展,企業需要做出決策的數量會不斷地增加,而決策質量的提高取決於決策方法的科學化。企業的決策水平提高了,企業的管理水平就一定會提高。
決策樹的適用範圍[1]
科學的決策是現代管理者的一項重要職責。我們在企業管理實踐中,常遇到的情景是:若幹個可行性方案制訂出來了,分析一下企業內、外部環境,大部分條件是己知的,但還存在一定的不確定因素。每個方案的執行都可能出現幾種結果,各種結果的出現有一定的概率,企業決策存在著一定的勝算,也存在著一定的風險。這時,決策的標準只能是期望值。即,各種狀態下的加權平均值。
針對上述問題,用決策樹法來解決不失為一種好的選擇。
決策樹法作為一種決策技術,已被廣泛地應用於企業的投資決策之中,它是隨機決策模型中最常見、最普及的一種規策模式和方法此方法,有效地控制了決策帶來的風險。所謂決策樹法,就是運用樹狀圖表示各決策的期望值,通過計算,最終優選出效益最大、成本最小的決策方法。決策樹法屬於風險型決策方法,不同於確定型決策方法,二者適用的條件也不同。應用決策樹決策方法必須具備以下條件:
①具有決策者期望達到的明確目標;
②存在決策者可以選擇的兩個以上的可行備選方案;
⑧存在著決策者無法控制的兩種以上的自然狀態(如氣候變化、市場行情、經濟發展動向等);
④不同行動方案在不同自然狀態下的收益值或損失值(簡稱損益值)可以計算出來;
⑤決策者能估計出不同的自然狀態發生概率。
決策樹的決策程式[1]
決策樹法的決策程式如下:
(1)繪製樹狀圖,根據已知條件排列出各個方案和每一方案的各種自然狀態。
(2)將各狀態概率及損益值標於概率枝上。
(3)計算各個方案期望值並將其標於該方案對應的狀態結點上。
(4)進行剪枝,比較各個方案的期望值,並標於方案枝上,將期望值小的(即劣等方案剪掉)所剩的最後方案為最佳方案。
決策樹法在企業決策中有著廣泛的應用。
決策樹是確定生產能力方案的一條簡捷的途徑。近年來出現的許多專門軟體包可以用來建立和分析決策樹,利用這些專門軟體包,解決問題就變得更為簡便了。
決策樹由決策結點、機會結點與結點間的分枝連線組成。通常,人們用方框表示決策結點,用圓圈表示機會結點,從決策結點引出的分枝連線表示決策者可作出的選擇,從機會結點引出的分枝連線表示機會結點所示事件發生的概率。
在利用決策樹解題時,應從決策樹末端起,從後向前,步步推進到決策樹的始端。在向前推進的過程中,應在每一階段計算事件發生的期望值。需特別註意:如果決策樹所處理問題的計劃期較長,計算時應考慮資金的時間價值。
計算完畢後,開始對決策樹進行剪枝,在每個決策結點刪去除了最高期望值以外的其他所有分枝,最後步步推進到第一個決策結點,這時就找到了問題的最佳方案。
下麵以南方醫院供應公司為例,看一看如何利用決策樹作出合適的生產能力計劃。
南方醫院供應公司是一家製造醫護人員的工裝大褂的公司。該公司正在考慮擴大生產能力。它可以有以下幾個選擇:1、什麼也不做;2、建一個小廠;3、建一個中型廠;4、建一個大廠。
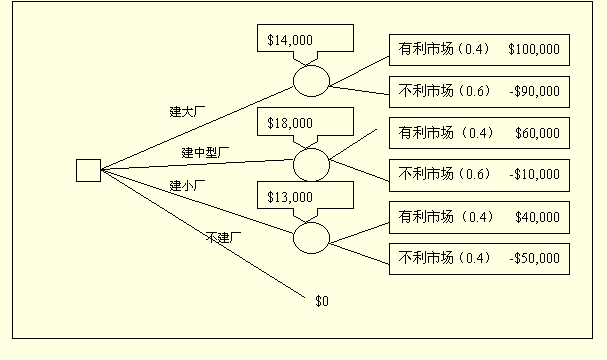
新增加的設備將生產一種新型的大褂,目前該產品的潛力或市場還是未知數。如果建一個大廠且市場較好就可實現$100,000的利潤。如果市場不好則會導致$90,000的損失。但是,如果市場較好,建中型廠將會獲得$ 60,000,小型廠將會獲得$40,000,市場不好則建中型廠將會損失$10,000,小型廠將會損失$5,000。當然,還有一個選擇就是什麼也不幹。最近的市場研究表明市場好的概率是0.4,也就是說市場不好的概率是0.6。參下圖:
在這些數據的基礎上,能產生最大的預期貨幣價值(EMV)的選擇就可找到。
- EMV(建大廠)=(0.4)*($100,000)+(0.6)*(-$90,000)=-$14,000
- EMV(中型廠)=(0.4) *($ 600,000))+(0.6)* (-$10,000)=+$18,000
- EMV(建小廠)=(0.4)* ($40,000)+(0.6)*(-$5,000)=+$13,000
- EMV(不建廠)=$0
根據EMV標準,南方公司應該建一個中型廠。
案例二:決策樹法在投標決策中的應用[2]
施工企業在同一時期內有多個工程項目可以參加投標,由於本企業資源條件有限,不可能將這些項目都承包下來,這類問題可用分析風險決策的決策樹法來進行定量分析。
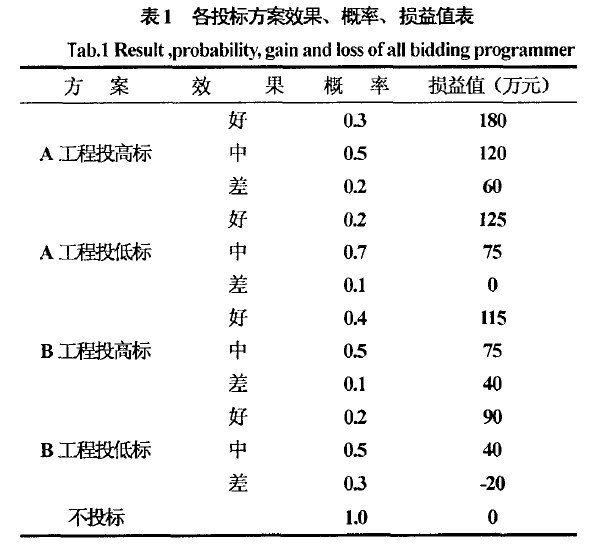
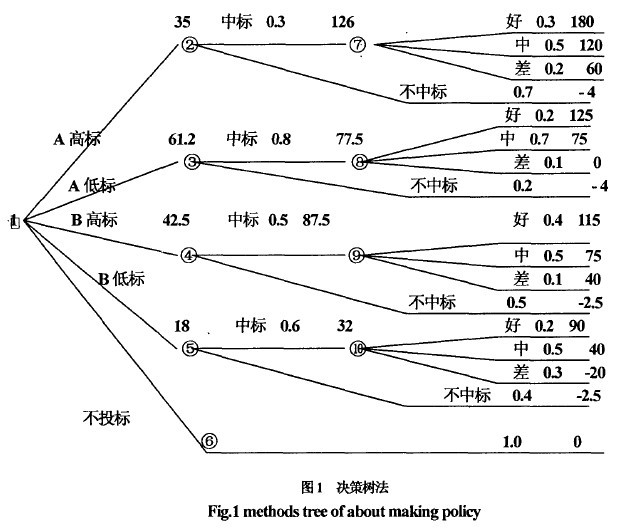
【例】某市屬建築公司面臨A, B兩項工程。因受本單位資源條件限制,只能選擇其中一項工程投標或者這兩項過程均不參加投標。根據過去類似工程投標的經驗數據,A工程投高標的中標概率為0.3,投低標的中標概率為0.8,編製該工程投標文件的費用為4萬元;B工程投高標的中標概率為0.5,投低標的中標概率為0.6,編製該工程投標文件的費用為2.5 萬元各方案承包的效果、概率、損益值如表1所示
計算決策樹上各機會點的期望值,並將計算出來的期望值標註在各機會點上方
機會點⑦: 180×0.3 + 120×0.5+ 60×0.2= 126
機會點②: 126×0.3 - 4×0.7=35
機會點⑧: 125×0.2+ 75×0.7 + 0×0.1=77.5
機會點③: 77.5×0.8- 4×0.2 = 61.2
機會點⑨: 115×0.4 + 75×0.5 + 40×0.1 = 87.5
機會點④: 87.5×0.5- 2.5×0.5 = 42.5
機會點⑩: 90×0.2 + 40×0.5 - 20×0.3 =32
機會點⑤: 32×0.6- 2.5×0.4=18
機會點⑥: 0
選擇最佳方案
方案枝上機會點③的期望值(61.2)最大方案(A低標) 為最佳方案,該施工企業應對A工程投低標。
下麵舉一實例說明其應用。某企業在下年度有甲、乙兩種產品方案可供選擇。每種方案都面I臨滯銷、一般、和暢銷三種市場狀態。各狀態的概率和損益值如下:
市場狀態
損益值方案滯銷 一般 暢銷 0.2 0.3 0.5 甲方案 20 70 100 乙方案 10 50 160
根據給出的條件運用決策樹法選擇一個最佳決策方案。
解題方法如下:
由此可以看出,決策樹法的決策過程就是利用了概率論的原理,並且利用一種樹形圖作為分析工具。其基本原理是用決策點代表決策問題,用方案分枝代表可供選擇的方案,用概率分枝代表方案可能出現的各種結果,經過對各種方案在各種結果條件下損益值的計算比較,為決策者提供決策依據。
本条目由以下用户参与贡献
蔓草寒烟,村姑,funwmy,山林,001,18°@鷺島,Zfj3000,Angle Roh,Palo,Vulture,Julia1,Dan,鲈鱼,Yixi,Taijiok,LiChunLeung,HEHE林,KAER,Gaoshan2013,袁扬,Lin,Tracy,Llyn.評論(共28條)
感謝Julia1的精彩貢獻
要是再能多舉幾個例子就更好了
添加了一個案例,希望對你有幫助
B工程投高標的中標概率為0.5,投低標的中標概率為0.5 這句話寫的怎麼和圖中的0.5 0.6不符啊。這是明顯的錯誤啊。
謝謝指正,錯誤之處已做修改~
MBA智庫百科是可以自由參與的百科,如有發現錯誤和不足,您也可以參與修改編輯,點擊條目上方的編輯進入即可參與,期待您的加入!~
一般都用什麼軟體化決策樹啊
我也有相同問題 有甚麼好用的工具呢?
我也有相同問題 有甚麼好用的工具呢?
可以用軟體思維導圖,X-Mind,或者谷歌線上應用Mind Map,Lucidchrt;其實word也能畫。
演算法有誤。例如那個如果投A標的話,需要先投入4萬,但是為什麼那個4萬隻在不中標的時候減,中標的時候不減呢?就算是中標了,這4萬也花出去了,那個2.5萬也是一樣的。這是明顯的錯誤。這個前期投入兩種解決方法,要麼最後統一減去,要麼在每一個狀態點計算的時候全都減去(excel計算時用的是這種辦法)。但是這個只是在不中標的時候減去明顯是不對的。還有就是圖了,首先面臨的第一個決策應該是投標還是不投標,然後投哪個標是投標這個決策下麵決策。
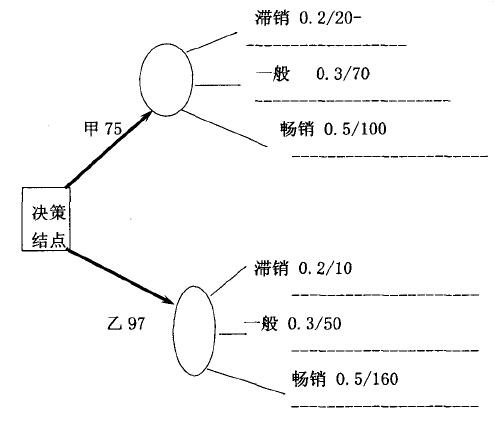








本題所舉例,題目不完整,但能基本反映決策樹的思路。