估計量
出自 MBA智库百科(https://wiki.mbalib.com/)
估計量(estimator)
目錄 |
估計量是指一個公式或方法,它告訴人們怎樣用手中樣本所提供的信息去估計總體參數。在一項應用中,依據估計量算出的一個具體的數值,稱為估計值。
估計量的優良性準則[1]
1.無偏性
估計量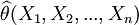 是一個隨機變數,對一次具體的觀察或試驗的結果,估計值可能較真實的參數值有一定偏離,但一個好的估計量不應總是偏小或偏大,在多次試驗中所得估計量的平均值應與參數的真值相吻合,這正是無偏性的要求。
是一個隨機變數,對一次具體的觀察或試驗的結果,估計值可能較真實的參數值有一定偏離,但一個好的估計量不應總是偏小或偏大,在多次試驗中所得估計量的平均值應與參數的真值相吻合,這正是無偏性的要求。
【定義1】 設(X1,X2,...,Xn)為來自總體X的樣本,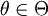 為總體的未知參數,
為總體的未知參數,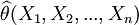 為θ的一個估計量.若對於任意
為θ的一個估計量.若對於任意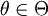 有
有
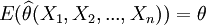 (1)
(1)
則稱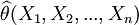 為θ的無偏估計量.記
為θ的無偏估計量.記
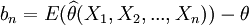
稱bn以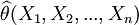 作為θ的估計的偏差,當
作為θ的估計的偏差,當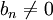 時,稱
時,稱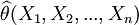 為θ的有偏估計量,若
為θ的有偏估計量,若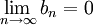 則稱
則稱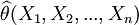 是θ的漸近無偏估計.
是θ的漸近無偏估計.
無偏性的意義是,用一個估計量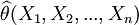 去估計未知參數θ,有時候可能偏高,有時候可能偏低,但是平均來說它等於未知參數θ。
去估計未知參數θ,有時候可能偏高,有時候可能偏低,但是平均來說它等於未知參數θ。
【定理1】 設對總體X,有E(X) = μ,D(X) = σ2從總體X中抽取樣本X1,X2,...,Xn用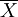 ,S2分別表示樣本均值和樣本修正方差,則
,S2分別表示樣本均值和樣本修正方差,則
(1)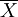 是 μ 的無偏估計量;
是 μ 的無偏估計量;
(2)S2是 σ2的無偏估計量.
證 由題設,E(Xi) = μ,D(Xi) = σ2(i = 1,2,...,n),且諸Xi獨立。於是有
(1)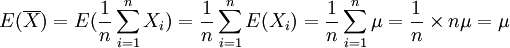 ,即
,即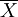 是總體均值μ的無偏估計量。
是總體均值μ的無偏估計量。
(2)因總體X的期望E(X) = μ和方差D(X) = σ2存在,則
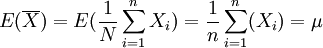
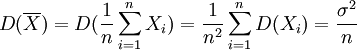
![E(S^2)=\frac{1}{n-1} E[\sum^n_{i=1} (X_i - \overline{X})^2]](/w/images/math/d/7/8/d7870773872a53bb6c53fc58b20e0b17.png)
![=\frac{1}{n-1} E [\sum^n_{i=1} X^2_i - n \overline{X}^2]](/w/images/math/b/8/d/b8dd3b0b250ce8b82a7cab8c3070c0d9.png)
![=\frac{1}{n-1} [\sum^n_{i=1} E(X^2_i) - nE (\overline{X}^2)]](/w/images/math/8/c/c/8cca806f63cb7446ba50f56cd1741aba.png)
![=\frac{1}{n-1} \sum^n_{i=1} \left\{D(X_i) + [E(X_i)]^2 \right\} - \frac{n}{n-1} \left\{D(\overline{X}) + [E(\overline{X})]^2 \right\}](/w/images/math/b/4/3/b4364b75d80eedf7bb8ce173f733b2b0.png)
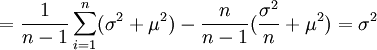
故S2是總體方差σ2的無偏估計量.
但對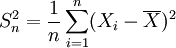 ,有
,有
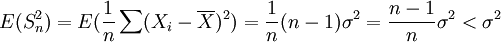
若n很大時,則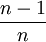 很接近1,表明
很接近1,表明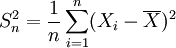 不是 σ2 的無偏估計,而是σ2的漸近無偏估計。
不是 σ2 的無偏估計,而是σ2的漸近無偏估計。
【例1】 設總體X的k階矩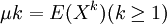 存在,(X1,X2,...,Xn)為來
存在,(X1,X2,...,Xn)為來
自總體X的樣本,試證明不論總體X服從什麼分佈,k階樣本矩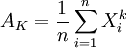 是k階總體矩μk的無偏估計.
是k階總體矩μk的無偏估計.
證 X1,X2,...,Xn與X同分佈,故有
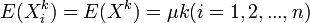
即有
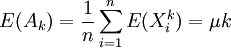
【例2】 設總體X服從參數為λ的指數分佈,其概率密度為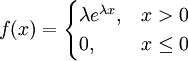
其中參數λ > 0 但未知,又設X1,X2,...,Xn為來自總體X的樣本,試證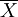 和nZ = n[min(X1,X2,...,Xn)]都是1 / λ的無偏估計.
和nZ = n[min(X1,X2,...,Xn)]都是1 / λ的無偏估計.
證 因E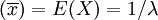 ,所以
,所以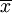 是1 / λ的無偏估計量.而Z = [min(X1,X2,...,Xn)]具有概率密度
是1 / λ的無偏估計量.而Z = [min(X1,X2,...,Xn)]具有概率密度
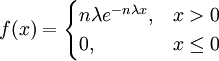
故知E(Z) = 1 / nλ,從而E(nZ) = 1 / λ,即nZ也是1 / λ的無偏估計量
此例結果表明,一個未知參數可以有不同的無偏估計量.值得註意,若 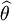 是 θ的無偏估計,g(θ)是θ的函數,
是 θ的無偏估計,g(θ)是θ的函數,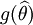 不一定是g(θ)的無偏估計.
不一定是g(θ)的無偏估計.
【例3】 試證樣本標準差S不是總體標準差 σ 的無偏估計.
證 因為σ2 = E(S2) = D(S) + [E(S)]2,註意到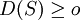 ,所以
,所以![\sigma^2 \ge [E(S)]^2](/w/images/math/0/0/1/00137301e2bd0355826750f6e7397bf3.png) ,於是
,於是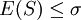 ,這表明儘管S2是σ2的無偏估計,但S不是總體標準差σ的無偏估計.用樣本標準差S去估計總體的標準差 σ ,平均來說是偏低了.
,這表明儘管S2是σ2的無偏估計,但S不是總體標準差σ的無偏估計.用樣本標準差S去估計總體的標準差 σ ,平均來說是偏低了.
2.有效性
用樣本統計量作為總體參數的估計量,其無偏性是重要的,但同一參數的無偏估計不是唯一的,還應該從中選取最好的.例如,從總體X中抽取樣本X1,X2,X3,則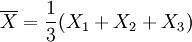 是總體均值 μ 的無偏估計.考慮E(Xi) = μ,則每個Xi也都是 μ 的無偏估計.還有
是總體均值 μ 的無偏估計.考慮E(Xi) = μ,則每個Xi也都是 μ 的無偏估計.還有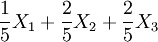 , 其數學期望也是μ,它也是μ的無偏估計。
, 其數學期望也是μ,它也是μ的無偏估計。
一般只要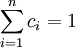 ,
, 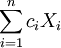 就是μ的無偏估計.這麼多無偏估計中哪一個更好一些呢?這就有了有效性的概念.
就是μ的無偏估計.這麼多無偏估計中哪一個更好一些呢?這就有了有效性的概念.
對於參數 θ 的無偏估計量,其取值應在真值附近波動,我們自然希望它與真值之間的偏差越小越好,也就是說無偏估計量的方差越小越好.
【定義2】 設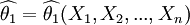 與
與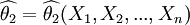 均為未知參數θ的無偏估計量,若
均為未知參數θ的無偏估計量,若
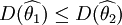 (2)
(2)
則稱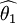 比
比 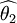 有效
有效
【定理2】 總體均值μ的所有線性無偏估計中,以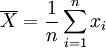 最為有效。
最為有效。
證 μ的所有線性無偏估計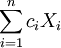 ,中
,中  其方差
其方差
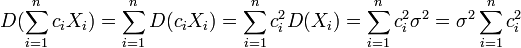
要求這個方差的最小值,相當於求函數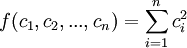 ,在條件
,在條件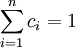 下的最小值.這是一個條件極值問題,用拉格朗日乘數法,令
下的最小值.這是一個條件極值問題,用拉格朗日乘數法,令
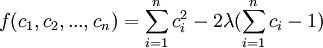
由 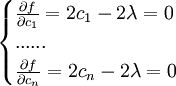
得 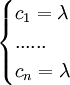
即c1 = c2 = ... = cn
代入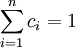 ,則
,則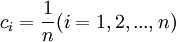 。
。
這是唯一駐點,應是極小值點,亦是最小值點,即當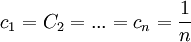 時,
時,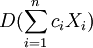 達到最小,即
達到最小,即
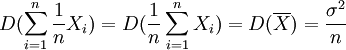
為方差最小值.這表明在總體均值μ的所有線性無偏估計中,以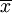 最為有效.
最為有效.
【例4】(續例2)在例2的條件下,試證當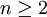 時,θ的無偏估計量
時,θ的無偏估計量 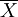 比無偏估計量nZ有效.
比無偏估計量nZ有效.
證 因為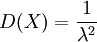 ,所以
,所以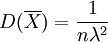 .再由Z的密度函數可得
.再由Z的密度函數可得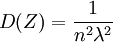 ,故有
,故有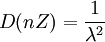 。當
。當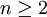 時
時 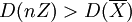 ,故
,故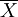 比nZ有效.
比nZ有效.
在θ的所有無偏估計量中,若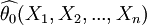 是具有最小方差的無偏估計量,則稱
是具有最小方差的無偏估計量,則稱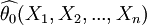 為θ的一致最小方差無偏估計量最優無偏估計量.
為θ的一致最小方差無偏估計量最優無偏估計量.
可以證明,無偏估計量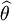 的方差
的方差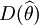 的下界D0(θ)為
的下界D0(θ)為
![D(\widehat{\theta}) \ge D_0 (\theta) = \frac{1}{nE[\frac{\partial}{\partial \theta} lnf (X, \theta)]^2} > 0](/w/images/math/3/6/f/36fe2c065800df9fa03d00f94f123b50.png)
當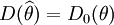 時,
時,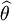 就是θ的最優無偏估計量.這裡,f(x,θ)表示連續型隨機變數的概率密度或離散型隨機變數的概率函數.
就是θ的最優無偏估計量.這裡,f(x,θ)表示連續型隨機變數的概率密度或離散型隨機變數的概率函數.
【例5】 設總體X服從參數為λ的泊松分佈,X1,X2,...,Xn是來自該總體的一個樣本,求參數λ的極大似然估計量 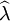 ,並證明
,並證明 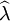 是參數λ的最優估計量.
是參數λ的最優估計量.
解 設樣本的一個觀察值為X1,X2,...,Xn,則似然函數
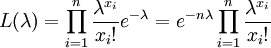
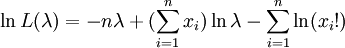
令
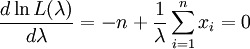
得 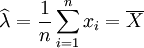
由於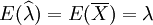 ,故
,故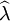 是參數λ的無偏估計量.
是參數λ的無偏估計量.
又因
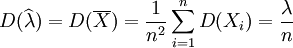
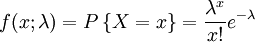
lnf(x;λ) = − λ + xlnλ − ln(x!)
![E \left\{[\frac{\partial}{\partial \lambda} \ln f(X; \lambda)]^2 \right\} = E[ \frac{1}{\lambda^2}(X - \lambda)^2] = \frac{1}{\lambda^2} E[X-E(X)]^2 = \frac{1}{\lambda^2} D(X) =\frac{1}{\lambda}](/w/images/math/8/0/4/8044f3743a6ea3a4c91e5647cdef30ca.png)
所以
![D_0(\widehat{\lambda}) = \frac{1}{nE \left\{ [\frac{\partial}{\partial \lambda} \ln f(X; \lambda)]^2 \right\}} = \frac{\lambda}{n}](/w/images/math/3/2/1/321736e4d9e6b5e799c89238553ef194.png)
因此,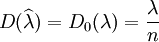 ,即
,即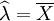 是參數λ的最優估計量
是參數λ的最優估計量
3.一致性
上面從無偏性和有效性兩個方面討論了選擇估計量的標準,但它們都是在固定樣本容量竹的前提下提出的.容易想象,如果樣本容量越大,樣本所含的總體分佈的信息應該越多,我們希望隨著樣本容量的增大,估計量的值能夠穩定於待估參數的真值,估計量的這種性質稱為一致性.
【定義3】設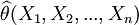 為參數θ的估計量,若對於任意
為參數θ的估計量,若對於任意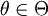 及任意ε > O,有
及任意ε > O,有
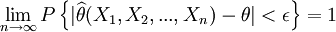 (3)
(3)
即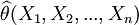 依概率收斂於θ,則稱
依概率收斂於θ,則稱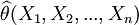 為θ的一致估計量(或相合估計量).
為θ的一致估計量(或相合估計量).
【例6】證明樣本k階原點矩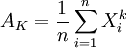 是總體k階原點矩
是總體k階原點矩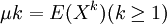 的一致估計.
的一致估計.
證由於X1,X2,...,Xn相互獨立與X同分佈,所以對任意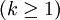 ,
, 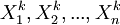 也相互獨立與Xk同分佈.因此,由大數定律,對於任意ε > 0,有
也相互獨立與Xk同分佈.因此,由大數定律,對於任意ε > 0,有
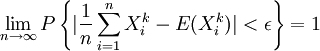
此表明Ak是 μk的一致估計量.
進而,若待估參數θ = g(μ1,μ2,...,μk),其中g(·)為連續函數,則θ的估計量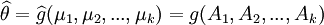 (這裡Ak為樣本k階原點矩)是θ的一致估計量。由此可證,樣本方差 S2 是總體方差σ2 的一致估計量。
(這裡Ak為樣本k階原點矩)是θ的一致估計量。由此可證,樣本方差 S2 是總體方差σ2 的一致估計量。
- ↑ 陳榮江,王建平主編.概率論與數理統計.科學出版社,2012.03







