相对收益
出自 MBA智库百科(https://wiki.mbalib.com/)
目录 |
相对收益又叫积极收益Alpha(简称α)、超额收益(ER)或执行收益(implementation return),通常用经理人增加Alpha的能力对他们进行评价,超额收益代表的是总收益超过无风险收益或基准收益的部分。
相对收益的表现形式[1]
- (一)直接差额形式
1.与无风险收益相比的绝对超额收益,分为简单形式和复合形式,分别为:
简单形式:ER=Rp − Rf=ER
复合形式:由于(1+Rp)=(1+Rf)(1+ER),则ER=\frac{1+Rp}{1+Rf} - 1
2.与基准收益相比的相对超额收益形式,又叫收益增加值(value added)
ER=Rp − RB(相当于β=1);ER为正,表明承担积极风险以获取超额收益而不是仅仅获得基准收益。
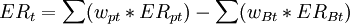
或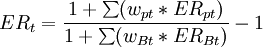
其中,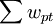 =1,
=1,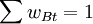
ERt表示组合在时间t超过基准组合的年化超额收益率,TE = σ(ERt)。
- (二)回归形式
采用Beta衡量的市场波动进行风险调整的Alpha指标,包括回归Alpha或Jensen’Alpha两类。但有时投资报告中的Alpha或Beta。并不表明对Alpha或Beta的计算采用的是收益回归分析还是超额收
益的CAPM模型计算出来的。因为回归方法与CAPM模型算出来的系数不同,含义解释也不同,因此在计算和汇报风险时,对其进行区分是很重要的。在基准代表的市场收益给定的情况下,回归系数是对投资组合预期收益的统计描述;CAPM模型得到的收益和Alpha系数分别是对组合收益的估计以及经理人超额收益的估计。具体包括:
1.回归Alpha。可以采用单指数或多因素模型回归:α = Rp − βRB + ε
在回归Alpha的分析中,决定系数R2反映了投资组合的分散化程度,便利起见将无风险利率处理为一常量,这样R2其实就是系统风险在总风险比重。
实证分析发现,我国证券投资基金中R2的值介于0.1529~0.1853之间,说明非系统的风险仍较大,组合的分散化程度较低。
R2愈大,总风险中系统风险的比例愈高,组合的分散化程度越高。
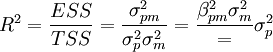 =系统风险/总风险
=系统风险/总风险
2.詹森Alpha:
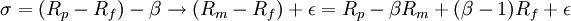
可见,简单回归Alpha中的基准收益RB包括市场组合Rm,完善的市场指数一般与基准是统一的。二者的区别在于,詹森Alpha比回归Alpha多了(β − 1)RfRf≤O这一项。此外,回归Alpha相当于β=1时的詹森Alpha。
此外,根据选取投资基准的不同,超额收益的表达式也不同。采取单一基准组合进行绩效评估时,超额收益率为:
Rp − Rf = αp + βp(Rm − Rf) + εp
采取多个基准组合进行绩效评估时,表达式为:
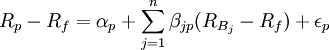
其中,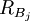 为第j个基准投资组合的收益率,βjp为目标投资组合超额收益率相对于第j个基准投资组合超额收益率的斜率系数。
为第j个基准投资组合的收益率,βjp为目标投资组合超额收益率相对于第j个基准投资组合超额收益率的斜率系数。
(三)总Alpha值(α)
业绩评价中的总风险调整Alpha指标是法玛将夏普比率中所使用的总风险调整法与詹森的收益率计算相结合提出的。公式为:
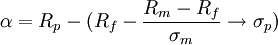
可见,总Alpha值足以资本市场线为依据进行计算的,这时组合的风险由其标准差表示。
- ↑ (美)皮尔逊著.风险预算[M].中信出版社,2011.03







