资本资产定价模型
出自 MBA智库百科(https://wiki.mbalib.com/)
资本资产定价模型(Capital Asset Pricing Model,CAPM)
目录 |
CAPM模型的提出[1]
马科维茨(Markowitz,1952)的分散投资与效率组合投资理论第一次以严谨的数理工具为手段向人们展示了一个风险厌恶的投资者在众多风险资产中如何构建最优资产组合的方法。应该说,这一理论带有很强的规范(normative)意味,告诉了投资者应该如何进行投资选择。但问题是,在20世纪50年代,即便有了当时刚刚诞生的电脑的帮助,在实践中应用马科维茨的理论仍然是一项烦琐、令人生厌的高难度工作;或者说,与投资的现实世界脱节得过于严重,进而很难完全被投资者采用——美国普林斯顿大学的鲍莫尔(william Baumol)在其1966年一篇探讨马科维茨一托宾体系的论文中就谈到,按照马科维茨的理论,即使以较简化的模式出发,要从1500只证券中挑选出有效率的投资组合,当时每运行一次电脑需要耗费150~300美元,而如果要执行完整的马科维茨运算,所需的成本至少是前述金额的50倍;而且所有这些还必须有一个前提,就是分析师必须能够持续且精确地估计标的证券的预期报酬、风险及相关系数,否则整个运算过程将变得毫无意义。
正是由于这一问题的存在,从20世纪60年代初开始,以夏普(w.Sharpe,1964),林特纳(J.Lintner,1965)和莫辛(J.Mossin,1966)为代表的一些经济学家开始从实证的角度出发,探索证券投资的现实,即马科维茨的理论在现实中的应用能否得到简化?如果投资者都采用马科维茨资产组合理论选择最优资产组合,那么资产的均衡价格将如何在收益与风险的权衡中形成?或者说,在市场均衡状态下,资产的价格如何依风险而确定?
这些学者的研究直接导致了资本资产定价模型(capital asset pricing model,CAPM)的产生。作为基于风险资产期望收益均衡基础上的预测模型之一,CAPM阐述了在投资者都采用马科维茨的理论进行投资管理的条件下市场均衡状态的形成,把资产的预期收益与预期风险之间的理论关系用一个简单的线性关系表达出来了,即认为一个资产的预期收益率与衡量该资产风险的一个尺度β值之间存在正相关关系。应该说,作为一种阐述风险资产均衡价格决定的理论,单一指数模型,或以之为基础的CAPM不仅大大简化了投资组合选择的运算过程,使马科维茨的投资组合选择理论朝现实世界的应用迈进了一大步,而且也使得证券理论从以往的定性分析转入定量分析,从规范性转入实证性,进而对证券投资的理论研究和实际操作,甚至整个金融理论与实践的发展都产生了巨大影响,成为现代金融学的理论基础。
当然,近几十年,作为资本市场均衡理论模型关注的焦点,CAPM的形式已经远远超越了夏普、林特纳和莫辛提出的传统形式,有了很大的发展,如套利定价模型、跨时资本资产定价模型、消费资本资产定价模型等,目前已经形成了一个较为系统的资本市场均衡理论体系。
夏普发现单个股票或者股票组合的预期回报率(Expected Return)的公式如下:
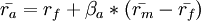
其中,rf(Risk free rate),是无风险回报率,纯粹的货币时间价值;
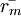 是市场期望回报率 (Expected Market Return),
是市场期望回报率 (Expected Market Return),
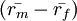 是股票市场溢价 (Equity Market Premium).
是股票市场溢价 (Equity Market Premium).
CAPM公式中的右边第一个是无风险收益率,比较典型的无风险回报率是10年期的美国政府债券。如果股票投资者需要承受额外的风险,那么他将需要在无风险回报率的基础上多获得相应的溢价。那么,股票市场溢价(equity market premium)就等于市场期望回报率减去无风险回报率。证券风险溢价就是股票市场溢价和一个β系数的乘积。
CAPM是建立在马科威茨模型基础上的,马科威茨模型的假设自然包含在其中:
1、投资者希望财富越多愈好,效用是财富的函数,财富又是投资收益率的函数,因此可以认为效用为收益率的函数。
4、影响投资决策的主要因素为期望收益率和风险两项。
5、投资者都遵守主宰原则(Dominance rule),即同一风险水平下,选择收益率较高的证券;同一收益率水平下,选择风险较低的证券。
CAPM的附加假设条件:
6、可以在无风险折现率R的水平下无限制地借入或贷出资金。
7、所有投资者对证券收益率概率分布的看法一致,因此市场上的效率边界只有一条。
8、所有投资者具有相同的投资期限,而且只有一期。
9、所有的证券投资可以无限制的细分,在任何一个投资组合里可以含有非整数股份。
11、所有投资者可以及时免费获得充分的市场信息。
13、投资者具有相同预期,即他们对预期收益率、标准差和证券之间的协方差具有相同的预期值。
上述假设表明:第一,投资者是理性的,而且严格按照马科威茨模型的规则进行多样化的投资,并将从有效边界的某处选择投资组合;第二,资本市场是完美/完全市场,没有任何磨擦阻碍投资。
- 优点
CAPM最大的优点在于简单、明确。它把任何一种风险证券的价格都划分为三个因素:无风险收益率、风险的价格和风险的计算单位,并把这三个因素有机结合在一起。
CAPM的另一优点在于它的实用性。它使投资者可以根据绝对风险而不是总风险来对各种竞争报价的金融资产作出评价和选择。这种方法已经被金融市场上的投资者广为采纳,用来解决投资决策中的一般性问题。
- 局限性
当然,CAPM也不是尽善尽美的,它本身存在着一定的局限性。表现在:
首先,CAPM的假设前提是难以实现的。比如,在本节开头,我们将CAPM的假设归纳为六个方面。假设之一是市场处于完善的竞争状态。但是,实际操作中完全竞争的市场是很难实现的,“做市”时有发生。假设之二是投资者的投资期限相同且不考虑投资计划期之后的情况。但是,市场上的投资者数目众多,他们的资产持有期间不可能完全相同,而且现在进行长期投资的投资者越来越多,所以假设二也就变得不那么现实了。假设之三是投资者可以不受限制地以固定的无风险利率借贷,这一点也是很难办到的。假设之四是市场无摩擦。但实际上,市场存在交易成本、税收和信息不对称等等问题。假设之五、六是理性人假设和一致预期假设。显然,这两个假设也只是一种理想状态。
其次,CAPM中的β值难以确定。某些证券由于缺乏历史数据,其β值不易估计。此外,由于经济的不断发展变化,各种证券的β值也会产生相应的变化,因此,依靠历史数据估算出的β值对未来的指导作用也要打折扣。总之,由于CAPM的上述局限性,金融市场学家仍在不断探求比CAPM更为准确的资本市场理论。目前,已经出现了另外一些颇具特色的资本市场理论(如套利定价模型),但尚无一种理论可与CAPM相匹敌。
按照CAPM的规定,Beta系数是用以度量一项资产系统风险的指针,是用来衡量一种证券或一个投资组合相对总体市场的波动性(volatility)的一种风险评估工具。也就是说,如果一个股票的价格和市场的价格波动性是一致的,那么这个股票的Beta值就是1。如果一个股票的Beta是1.5,就意味着当市场上升10%时,该股票价格则上升15%;而市场下降10%时,股票的价格亦会下降15%。
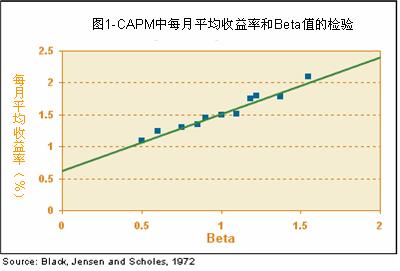
Beta是通过统计分析同一时期市场每天的收益情况以及单个股票每天的价格收益来计算出的。1972年,经济学家费歇尔·布莱克 (Fischer Black)、迈伦·斯科尔斯(Myron Scholes)等在他们发表的论文《资本资产定价模型:实例研究》中,通过研究1931年到1965年纽约证券交易所股票价格的变动,证实了股票投资组合的收益率和它们的Beta间存在着线形关系。
当Beta值处于较高位置时,投资者便会因为股份的风险高,而会相应提升股票的预期回报率。举个例子,如果一个股票的Beta值是2.0,无风险回报率是3%,市场回报率(Market Return)是7%,那么市场溢价(Equity Market Premium) 就是4%(7%-3%),股票风险溢价(Risk Premium)为8% (2X4%,用Beta值乘市场溢价),那么股票的预期回报率则为11%(8%+3%, 即股票的风险溢价加上无风险回报率)。
以上的例子说明,一个风险投资者需要得到的溢价可以通过CAPM计算出来。换句话说,我们可通过CAPM来知道当前股票的价格是否与其回报相吻合。
2.资产风险溢酬=风险的价格×风险的数量
3.风险的数量 = β(SML的斜率)。
4.风险的价格 = E(Rm) − Rf
5.证券市场线(SML)的斜率等于市场风险贴水,当投资人的风险规避程度愈高,则SML的斜率愈大,证券的风险溢酬就愈大,证券的要求报酬率也愈高。
6.当证券的系统性风险(用β来衡量)相同,则两者之要求报酬率亦相同,证券之单一价格法则。
CAPM给出了一个非常简单的结论:只有一种原因会使投资者得到更高回报,那就是投资高风险的股票。不容怀疑,这个模型在现代金融理论里占据着主导地位,但是这个模型真的实用么?
在CAPM里,最难以计算的就是Beta的值。当法玛(Eugene Fama)和肯尼斯·弗兰奇(Kenneth French) 研究1963年到1990年期间纽约证交所,美国证交所,以及纳斯达克市场(NASDAQ)里的股票回报时发现:在这长时期里Beta值并不能充分解释股票的表现。单个股票的Beta和回报率之间的线性关系在短时间内也不存在。他们的发现似乎表明了CAPM并不能有效地运用于现实的股票市场内!
事实上,有很多研究也表示对CAPM正确性的质疑,但是这个模型在投资界仍然被广泛的利用。虽然用Beta预测单个股票的变动是困难,但是投资者仍然相信Beta值比较大的股票组合会比市场价格波动性大,不论市场价格是上升还是下降;而Beta值较小的股票组合的变化则会比市场的波动小。
对于投资者尤其是基金经理来说,这点是很重要的。因为在市场价格下降的时候,他们可以投资于Beta值较低的股票。而当市场上升的时候,他们则可投资Beta值大于1的股票上。
对于小投资者的我们来说,我们实没有必要花时间去计算个别股票与大市的Beta值,因为据笔者了解,现时有不少财经网站均有附上个别股票的 Beta值,只要读者细心留意,但定可以发现得到。
1.应用资本资产定价理论探讨风险与报酬之模式,亦可发展出有关证券均衡价格的模式,供作市场交易价格之参考。
2.所谓证券的均衡价格即指对投机者而言,股价不存在任何投机获利的可能,证券均衡价格为投资证券的预期报酬率,等于效率投资组合上无法有效分散的等量风险,如无风险利率为5%,风险溢酬为8%,股票β系数值为0.8,则依证券市场线所算该股股价应满足预期报酬率11.4%,即持有证券的均衡预期报酬率为:
E(Ri) = RF + βi[E(Rm) − Rf]
3.实际上,投资人所获得的报酬率为股票价格上涨(下跌)的资本利得(或损失),加上股票所发放的现金股利或股票股利,即实际报酬率为:
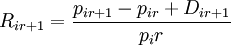
4.在市场均衡时,预期均衡报酬率应等于持有股票的预期报酬率
![R_F+\beta_i[E(R_m)-R_F]=\frac{E(P_{ir+1}-P_{ir}+E(D_{ir+1}))}{P_{ir}}](/w/images/math/e/5/9/e59af741bf0906650166acb2f4bb32ee.png)
5.若股票的市场交易价格低于此均衡价格,投机性买进将有利润,市场上的超额需求将持续存在直到股价上升至均衡价位;反之若股票的交易价格高于均衡价格,投机者将卖出直到股价下跌达于均衡水准。
- 1.CAPM的假设条件与实际不符:
a.完全市场假设:实际状况有交易成本,资讯成本及税,为不完全市场
b.同质性预期假设:实际上投资人的预期非为同质,使SML信息形成一个区间.
c.借贷利率相等,且等于无风险利率之假设:实际情况为借钱利率大于贷款利率。
d.报酬率分配呈常态假设,与事实不一定相符
- 2.CAPM应只适用于资本资产,人力资产不一定可买卖。
- 3.估计的β系数指代表过去的变动性,但投资人所关心的是该证券未来价格的变动性。
- 4.实际情况中,无风险资产与市场投资组合可能不存在。
- ↑ 吴晓求著.证券投资学.中国人民大学出版社,2009.02.
本条目由以下用户参与贡献
蔓草寒烟,苦行者,Vulture,Angle Roh,村姑,沙漠之鹰,山林,funwmy,Zfj3000,Kane0135,Lolo,Sixdays,Dan,Cabbage,Chenfengxixi,鲈鱼,Steven wyd,Shenp382,风行水使,Yixi,HEHE林,jane409,连晓雾,林巧玲,周翰君,开荒的木头人,Mis铭,刘维燎,151****3899,156****8892.评论(共59条)
谢谢NjuWgl的重新整理
我有一个疑问。CAPM是否能够有效的评估NPV。通过以上的材料,我们可以发现,CAPM会过分的夸大风险。从而使投资者失去许多赚钱的机会。而且CAPM本身就有很多疑问。但大家都在用它。这到底说明了什么?我有点不太理解。
The model was introduced by Jack Treynor (1961, 1962),[1] William Sharpe (1964), John Lintner (1965a,b) and Jan Mossin (1966) independently, building on the earlier work of Harry Markowitz on diversification and modern portfolio theory.
这是wiki上面的说明,如果只是断章起义的说是夏普写的那很不尊重其他有份建立这个模型的大师
真的很不错,中文就是比英文容易懂啊!
有这个感觉。
这算解析个毛啊,谁能告诉我 β值如何求,计算公式是什么?
你算什么东西
这算解析个毛啊,谁能告诉我 β值如何求,计算公式是什么?
什么都不懂就吐槽
这算解析个毛啊,谁能告诉我 β值如何求,计算公式是什么?
1.采用历史数据,证券收益对市场收益线性回归,回归方程的斜率即为所求。 2.根据公式贝塔值为证券收益与市场收益之间协方差与市场组合方差之比。 多看书,少聒噪
为什么capm 过分夸大风险了
网页中的latex公式一直显示不出来,用红色的大字显示:解析失败 (PNG 转换失败; 请检查是否正确安装了 latex, dvips, gs 和 convert): 然后后面明显是写网页代码的时候敲进去的公式格式。我在chrome上装了mathanywhere插件也没有用,请问该如何解决?









很详细,很有帮助~