价格水平规制

出自 MBA智库百科(https://wiki.mbalib.com/)

价格水平规制(Price level regulation)

　　价格规制是在自然垄断和存在信息偏在的领域，政府为了保证资源的有效配置和服务的公平供给，对价格水平和价格结构进行规制，以限制垄断企业制定垄断价格。价格规制包括价格水平规制和价格结构规制。

　　对于自然垄断行业而言，价格水平的高低，不仅影响着企业的生产经营行为和生产经营效果，也直接关系到资源配置效率和社会分配效率。因此，价格水平规制的目标主要有四个方面：

　　1、优化资源配置；

　　2、是促进社会分配效率；

　　3、是激励企业生产；

　　4、是保障企业利益。

　　自然垄断行业的价格水平规制目标与定价方式有着密切的联系。如前文所述，在选择定价方式和价格水平时，不仅要兼顾社会目标和企业目标，还要充分考虑到社会目标内部各分目标的实现情况。

　　1、企业自行定价

　　在没有政府干预的条件下，企业根据利润最大化原则，会按照边际成本等于边际收益来确定价格水平.

　　2、边际成本定价方式

　　根据经济学原理，为实现促进社会分配效率目标，应当是边际成本曲线MC与需求曲线DD（平均收益曲线）的交点决定的规制价格水平,这从理论上讲能保证分配效率。

　　3、平均成本定价方式

　　没有政府干预的条件下，企业自行定价会导致过高的垄断价格；边际成本与平均收益决定的价格又过低，能否在二者中间找出最优的定价方式呢？用平均成本曲线AC与平均收益曲线AR（DD）来决定价格水平，能缓解这一矛盾。

　　从以上分析可以看出，对自然垄断行业价格水平进行规制，并不存在理论上的最优定价方式和价格水平。其主要原因是规制目标多元化，且涉及到价值判断问题而无法量化，不同的人、不同的群体会给不同的目标赋予不同的权重。笔者认为按平均成本定价更优一些，是基于综合考虑这些目标的实现情况，当然也有个人的价值判断，从而得出的结论。

　　由于理论上并不存在最优的定价方式，在实践中就表现出世界各国对价格水平进行规制都存在操作上的困难。当前，有两种比较有典型意义的价格水平规制模型，即美国的投资回报率价格规制模型和英国的最高限价规制模型。

　　美国对自然垄断产业实行投资回报率价格规制具有悠久的历史。具体做法通常是被规制企业首先向规制者提出要求提高价格（或投资回报率）的申请，规制机构经过一段考察期，根据影响价格的因素变化情况，对企业提出的价格（或投资回报率）水平作必要调整，最后确定企业的投资回报率，作为企业在某一特定时期内定价的依据。如果企业只生产一种产品（或服务），则投资回报率价格规制模型为：

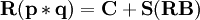
　　英国的最高限价规制采取RPI-X模型，RPI表示价格指数，即通货膨胀率，X是由规制者确定的，在一定时期内生产效率增长的百分比。例如，如果某年通货膨胀率是5%（即RPI=5%），X固定为3%（即X=3%），那么，企业提价的最高幅度是2%。这个简单的价格规制模型意味着，企业在任何一年中制定的名义价格取决于RPI和X的相对值。如果RPI-X是一个负数，则企业必须降价，其幅度是RPI-X的绝对值。这样，如某企业本期的价格为Pt,则下期的规制价格(Pt+1)为：

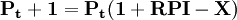
　　针对中国的实际情况，并借鉴经济发达国家的价格规制模型，一些学者构建了中国自然垄断行业价格水平规制模型。其中，较为有代表意义的有两种类似的价格模型，一个是“成本——效率”模型;另一个是“成本——效率——质量”模型。

　　1、“成本——效率”模型

　　“成本——效率”模型的计算公式为：

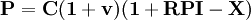
　　将该式展开则为：

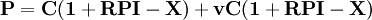
　　式中，P为“成本—效率”模型的价格，C为正常年度的平均单位成本，v为成本利润率，RPI为零售物价指数，X为政府规定的生产效率增长率。

　　在该价格模型中，C(1+RPI-X)为成本上限控制项，在制定规制价格时，首先要考虑成本情况和成本变动情况。在影响成本的众多因素中， RPI是一个综合性因素，随着RPI的变化，企业的原材料、工资成本等也会发生一定的变化，C×RPI正是为了适应这种变化而在价格上作出的相应调整。正常情况下，RPI是一个正数，因此，C×RPI表现为成本增量。同时，为了促使企业提高生产效率，降低成本，政府为企业规定了一个生产效率增长率（成本下降率）X，CX为成本减量。如果RPI-X>0，则规制价格中，成本可以增加，增量为C(RPI-X)；反之，RPI-X<0，成本则必须减少，减量为C(RPI-X)的绝对值。vC(1+RPI-X)是在当前的成本约束下的利润水平，v为政府核准的成本利润率，可以理解为资本的投资回报率，以此保障企业利益，维持扩大再生产和追加投资的能力。

　　这一价格模型的实质是，将美国投资回报率价格规制模型和英国最高限价模型综合起来，取其各自的优点，使价格水平规制更具合理性。一方面，X是由政府规定的，企业要取得较多的利润，必须使其实际的生产效率增长率大于X，这就会刺激企业自觉提高生产效率、努力降低成本。另一方面，vC决定了企业的投资利润水平，虽然这里的C有不断下降的硬性约束，但也能一定程度上保证企业增加投资、扩大供给，更好地满足市场需求的积极性。

　　2、“成本——效率——质量”模型

式中，Pt+1为下一期的规制价格，Ct为本期式中，Pt+1为下一期的规制价格，Ct为本期单位成本，RPI为零售价格指数；X为生产效率增长率，r为销售利润率，Q为产品与服务质量系数。

　　与“成本—效率”模型相比，该模型有以下三个方面的改进或调整：

　　第一，强调了时间因素。强调时间因素的意义在于，突出了成本降低的时序性，要求成本逐年递减，从而进一步强化了成本约束。这样，在使用该模型时，如果C0被确定，在其他因素不变的条件下，以后各个年份的成本上限C1、C2……Ct便相应确定，实际成本逐年降低，降幅为X。

　　第二，采用销售利润率决定企业利润水平。在该模型中，Pt+1×r为单位产品的销售利润，r为销售利润率；而在前一个模型中，Cv为单位产品的成本利润，v为成本利润率。

　　第三，引入质量因素。质量因素的引入，是该模型最大的改进，它将价格水平规制和产品或服务质量规制紧密地结合在一起，目的是促使企业在成本上限控制的情况下，必须符合政府规定的产品质量标准，并提供优质的服务。

　　很显然，在上述两个价格模型中，对于Ct（C）、RPI、X、r（v）、Q等因素在实践中的合理确定和科学取值，是价格规制成功与否的关键。 Ct 的确定是基础，特别是初始C0的取值尤为重要。因此，在事业模型时，一定要根据各个自然垄断行业的不同技术特征和企业当前的生产经营状况科学核定成本水平。零售价格指数RPI可能不能完全反映企业成本因受价格影响而发生的变化，因此，需要针对具体情况对RPI进行相应的微调，以较好地反映成本变化情况。参数X值的确定是一个难点，需考虑以下几个主要因素：

• 企业现有生产效率与该产业先进生产效率的差距，如果现有生产效率较低，则提高生产效率的潜力就大，X值也应较大；
• 该产业的技术进步率，技术进步愈快，X值应较大；
• 当前企业生产经营管理状况，提高管理效率的潜力越大，X也应较大

　　生产效率增长率X值，应该是企业通过努力可以达到甚至超越的，以刺激企业努力降低成本。r值的确定，可以综合考虑全社会平均利润率、其他行业平均利润率、长期国债（10年期）利率等指标合理取值。质量参数Q的最大值一般为1，如果企业提供的产品达到政府规定标准，且服务质量较高，则Q值为1；否则，Q值应当小于1。

　　需要指出的是，上述各因素的取值并非一成不变，应根据技术经济条件的变化及时调整。特别是当前我国自然垄断行业产品的规制价格水平还不够合理，各因素取值的调整可能更为频繁。