R/S分析法
出自 MBA智库百科(https://wiki.mbalib.com/)
R/S分析法(R/S analysis method)
目錄 |
R/S分析法通常用來分析時間序列的分形特征和長期記憶過程,最初由英國水文學家赫斯特(Hurst,1951年)在研究尼羅河水壩工程時提出的方法。後來,它被用在各種時間序列的分析之中。
曼德爾布羅特(Mandelbrot)在1972年首次將R/S分析應用於美國證券市場,分析股票收益的變化,彼得斯(Peters)把這種方法作為其分形市場假說最重要的研究工具進行了詳細的討論和發展,並做了很多實證研究。R/S分析方法的基本內容是:對於一個時間序列{xt},把它分為N個長度為A的等長子區間,對於每一個子區間,設:
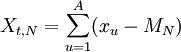 (1)
(1)
其中,Mn為第n個區間xu的平均值,Xt,n為第n個區間的累計離差。令:
R = max(Xt,n) − min(Xt,n) (2)
若以S表示xu序列的標準差,則可定義重標極差R/S,它隨時間而增加。Hurst通過長時間的實踐總結,建立瞭如下關係:
R / S = K(n)H (3)
對(3)式相邊取對數,得到(4)式:
log(R / S)n = Hlog(n) + log(K) (4)
因此,對log(n)和log(R / S)n進行最小二乘法回歸就可以估計出H的值。
在對周期迴圈長度進行估計時,可用Vn統計量,它最初是Hurst用來檢驗穩定性,後來用來估計周期的長度。
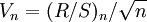 (5)
(5)
計算H值和Vn的目的是為了分析時間序列的統計特性。Hurst指數可衡量一個時間序列的統計相關性。當H=0.5時,時間序列就是標準的隨機游走,收益率呈正態分佈,可以認為現在的價格信息對未來不會產生影響,即市場是有效的。當0.5≤H<1時,存在狀態持續性,時間序列是一個持久性的或趨勢增強的序列,收益率遵循一個有偏的隨機過程,偏倚的程式有賴於H比0.5大多少,在這種狀態下,如果序列前一期是向上走的,下一期也多半是向上走的。當0<H≤0.5時,時間序列是反持久性的或逆狀態持續性的,這時候,若序列在前一個期間向上走,那麼下一期多半向下走。
對於獨立隨機過程的時間序列來說,Vn關於log(n)的曲線是一條直線。如果序列具有狀態持續性,即當H>0.5時,Vn關log(n)是向上傾斜的;如果序列具有逆狀態持續性,即當H<0.5 時,Vn關於log(n)是向下傾斜的。當Vn 圖形形狀改變時,就產生了突變,長期記憶消失。因此,用Vn關於log(n)的關係曲線就可以直觀地看出一個時間序列某一時刻的值 對以後值的影響時間的界限。
為了測算序列對隨機游走的偏離,Peters還引入了E(R / S)n統計量,它的計算公式為:
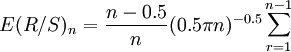 (6)
(6)
對於一個時間序列,當H≠0.5時,對應於方差比分析中VR(q)≠1時的情況,收益率不再呈正態分佈,時間序列各個觀測值之間不是互相獨立的,後面的觀測值都帶著在它之前的觀測值的“記憶”,這就是我們所說的長期記憶性,從理論上來說它是存在的。隨時間延長,前面觀測值對後面觀測值影響越來越少。因此,時間序列是一長串相互聯繫的事件疊加起來的結果。為了描述現在對未來的影響,Mandelbrot引進了一個相關性度量的指標CM,它表示的意思和H是對應的。
CM = 2(2H − 1) − 1 (7)
其中CM表示在期間M上的相關性。所以,當H=0.5時,序列不相關;當C>0時,序列正相關;當C<0時,序列負相關。
在檢驗過程中,我們使用對數收益率,即對502個周收盤價數據按公式(8)進行處理,得到501個數據組成的周收益率序列。為了消除序列的線性依賴,一般分析收益率序列的AR(1)殘差,因為線性依賴會使分析偏離Hurst指數或導致第一類錯誤的發生。以St為因變數,St − 1為自變數,St對St − 1進行回歸,就可以得到St的殘差序列。
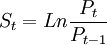 (8)
(8)
- Xt = St − (a + bSt − 1) (9)
按照以上方法,我們用Gauss5.0編寫電腦程式進行計算,得到表1的結果。
表1:滬深兩市周收益率序列(R/S)n計算結果
| n | log(n) | R/S | log(R/S) | E(R/S) | V統計量 | ||
|---|---|---|---|---|---|---|---|
| R/S | E(R/S) | ||||||
| 上海 | 4 | 1.3863 | 1.4431 | 0.3668 | 1.1552 | 0.7216 | 0.5776 |
| 5 | 1.6094 | 1.7119 | 0.5376 | 1.4584 | 0.7656 | 0.6522 | |
| 10 | 2.3026 | 3.0025 | 1.0994 | 2.6503 | 0.9495 | 0.8381 | |
| 20 | 2.9957 | 4.8036 | 1.5694 | 4.3247 | 1.0741 | 0.9670 | |
| 25 | 3.2189 | 5.1380 | 1.6367 | 4.9961 | 1.0276 | 0.9992 | |
| 50 | 3.9120 | 8.4717 | 2.1367 | 7.6185 | 1.1981 | 1.0774 | |
| 100 | 4.6052 | 11.6460 | 2.4550 | 11.3103 | 1.1646 | 1.1310 | |
| 125 | 4.8283 | 13.8308 | 2.6269 | 12.7952 | 1.2371 | 1.1444 | |
| 250 | 5.5215 | 20.2101 | 3.0062 | 18.6138 | 1.2782 | 1.1772 | |
| 深圳 | 4 | 1.3863 | 1.4542 | 0.3744 | 1.1552 | 0.7271 | 0.5776 |
| 5 | 1.6094 | 1.7226 | 0.5439 | 1.4584 | 0.7704 | 0.6522 | |
| 10 | 2.3026 | 2.8526 | 1.0482 | 2.6503 | 0.9021 | 0.8381 | |
| 20 | 2.9957 | 4.5795 | 1.5216 | 4.3247 | 1.0240 | 0.9670 | |
| 25 | 3.2189 | 5.3673 | 1.6803 | 4.9961 | 1.0735 | 0.9992 | |
| 50 | 3.9120 | 8.5869 | 2.1502 | 7.6185 | 1.2144 | 1.0774 | |
| 100 | 4.6052 | 13.5896 | 2.6093 | 11.3103 | 1.3590 | 1.1310 | |
| 125 | 4.8283 | 14.5547 | 2.6779 | 12.7952 | 1.3018 | 1.1444 | |
| 250 | 5.5215 | 23.6086 | 3.1616 | 18.6138 | 1.4931 | 1.1772 | |
表2:滬深兩市Hurst指數估算表
| 區間 | 截距 | Hurst指數 | 估計的標準差 | 觀察個數 | R2 | P 值(>F) | CM | |
|---|---|---|---|---|---|---|---|---|
| 上海 | 4≤n≤250 | -0.4250 | 0.6340 | 0.0734 | 9 | 0.9945 | 0.0000 | 0.204 |
| 4≤n≤20 | -0.5966 | 0.7116 | 0.0530 | 4 | 0.9938 | 0.0002 | 0.341 | |
| 25≤n≤250 | -0.0124 | 0.5446 | 0.0334 | 5 | 0.9944 | 0.0028 | 0.064 | |
| 深圳 | 4≤n≤250 | -0.5166 | 0.6721 | 0.0380 | 9 | 0.9987 | 0.0000 | 0.269 |
| 4≤n≤100 | -0.5684 | 0.6943 | 0.0169 | 7 | 0.9997 | 0.0000 | 0.309 |
註:因為在深圳證券市場的區間125≤n≤250 內,只有兩個觀測數據,回歸結果不具有現實意義,故未加列示。
按照(4)式分別對滬深兩市的log(n)和log(R/S)進行回歸,得到上海證券市場的Hurst指數為0.6340,深圳證券市場的Hurst指數為0.6721(表2),都明顯大於隨機游走假設的臨界值0.5,說明滬深兩市都存在明顯的持久性和分形結構。股票的周收益序列不同於普通的隨機游走,是一個有偏的隨機游走過程,這是因為序列的前後的記憶性在起作用。
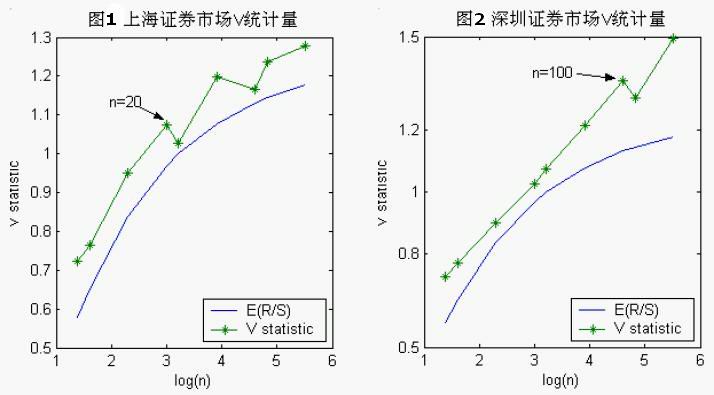
圖1、2分別給出了滬深兩市V統計量相對於log(n)的變化趨勢。因為V統計量是(R/S)n相對於n0.5的變化率,所以當時間序列呈現出持續性(H>0.5)時,比率就會增加,V統計量曲線就會一直上升;如果序列呈現出隨機游走(H=0.5)或反持續性(H<0.5),V統計量將大致保持不變或單調下降。所以,V統計量曲線由上升轉而為保持大致不變或下降的分界點就是序列長期記憶的消失點。如圖1、2所示,滬深兩市分別在n=20和n=100處V統計量停止增長,所以,n=20和n=100即為兩個市場的分界點。分別就分界點前後的log(n)和log(R/S)序列進行回歸,可以計算分界點前後的Hurst指數(表2)。以上海證券市場為例,分界點前,Hurst指數為0.7116,相關係數CM為34.1%,遠高於隨機游走時的情況;分界點後,Hurst指數僅有0.5446,接近隨機游走時的0.5。這表明序列中非周期成分是存在的,分界點處n=20,即20周就是非周期迴圈的長度。這與文獻[1]中對上證綜合指數從1990.3.26至1999.3.26間的周收益率進行分析所得結果是相同的。同樣,100周則是深圳證券市場的非周期迴圈的長度。文獻[2]中,對深證1991年—1998年的日收益率進行了R/S分析,雖然計算出Hurst指數為0.643,大於0.5,但沒有得出深證的非周期迴圈的長度,這可能與樣本期太短有關,由這裡的結果來看,說明深證的非周期迴圈的長度確實比上證要長得多。
- [1] 史永東. 上海證券市場的分形結構[J]. 預測, 2000, 5:78-80
- [2] 徐龍炳, 陸蓉. R/S分析探索中國股票市場的非線性[J]. 預測, 1999, 2:59-62
- 劉永濤. 中國股票市場長期記憶性的實證研究[J]








St = Ln(Pt / Pt − 1) (8) 這段錯誤 應為 St = In(Pt / Pt − 1) (8)