資本配置線
出自 MBA智库百科(https://wiki.mbalib.com/)
資本配置線(Capital Allocation Line,CAL)
目錄 |
與投資組合具有相同特征、不同風險資產權重的一系列投資組合的期望收益與標準差配對集合構成了投資可行集,由它們連接而成的直線,叫資本配置線。
資本配置線是引入無風險借貸後,將一定量的資本在某一特定的風險資產組合與無風險資產之間分配,描述所有可能的新組合的預期收益與風險之間關係的線條。由於無風險資產與風險資產之間的協方差為0,因此,在二維坐標系中,資本配置線就是無風險資產回報的點(出現在縱軸上)與風險資產的點(風險資產在二維坐標內,收益比無風險資產高)的連線。當投資人強調安全性時,會增加無風險資產的持有;當投資人強調收益性時,會增加對風險資產的持有,對應的組合點就在資本配置線上移動。
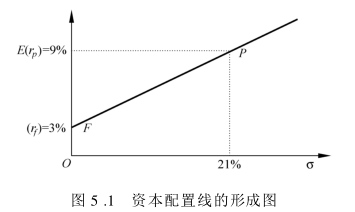
資本配置線的形成[1]
如果我們定義坐標的橫軸為反映風險的標準差,豎軸為資產組合的期望收益。那麼,我們可以說,無風險資產組合的期望收益-風險組合的幾何表達是上述坐標的豎軸的一點[E(rp)=3%,σp=0],因為無風險資產組合的標準差為0。風險資產組合P的幾何表達是另一個點[E(rp)=9%,σp=21%]。這樣,如果投資者的選擇是將全部投資都投向風險資產,即y=1,他所選擇的就是資產組合P,他的期望收益與標準差就是E(rp)=9%,σp=21%。如果投資者的選擇是將全部投資都投向無風險資產,即1-y=1,他所選擇的就是資產組合F,他的期望收益與標準差就是E(rp)=3%,σp=0。在期望收益與標準差的組合圖上連這兩點成一條直線,我們稱這條線為資本配置線。這條直線的斜率為[E(rp)-rf]/σp(增量/自變數),即6/21。圖5.1是資本配置線的圖形。
資本配置線的含義[1]
我們已知資本配置線上的兩個點是投資者資本配置的兩個極端點,即或者將全部投資都投向風險資產,或者將全部投資都投向無風險資產。在這兩點之間的資本配置線上的任意一點反映了投資者的某一種既有風險資產投資,又有無風險資產投資的資產組合,以及這一資產組合的期望收益和標準差的情況。從資本配置線上標準差為0的點開始沿線右移,線上離0點越遠的點代表了一個風險資產在全部資產組合中占比例更大的一種資產組合。因此,從資本配置線上可以直觀地看到,隨著風險資產在全部資產組合中所占比例的不斷增長,全部資產組合的風險(標準差)也越來越大。由於直線的斜率為6/21=0.29,因此,每增加1單位額外的風險,可以獲得0.29單位的額外收益。換句話說,就是每增加1單位額外的收益,將增加3.5(21/6=3.5)單位風險。
資本配置線的數學表達[1]
為了給出資本配置線的進一步的數學表達式,我們將σc=yσp=21y式進行整理,有y = σc / σp,將y代入E(rc)=yE(rp)+(1-y)rf=rf+y[E(rp)-rf]=3%+y(9%-3%)式,有
E(rc)=rf + y[E(rp) − rf] = rf + (σc / σp)[E(rp) − rf]
=3+(6/21)σc.................(5.7)
從式中可以看到,資產組合的期望收益作為其標準差的函數是一條直線,其截距為rf,斜率為6/21。斜率S的數學表達式為
S=[E(rp)-rf]/σp =6/21...........(5.8)
有了資本配置線的截距和斜率的數學表達,我們就可以對資本配置線的幾何表達有更深入的認識。因此,我們現在可以明確,資本配置線反映了投資者所有可行的風險收益資產組合。由於直線的斜率反映了在選擇資產組合時,每增加一單位標準差會增長的期望收益。因此,該斜率也可稱為酬報與波動性比率(reward-to-variabilityratio)。我們一般認為這個值較大些好,因為這個值越大,就意味著資本配置線越陡,即增加一單位風險可以增加更多的期望收益。
如果選擇將全部投資投向風險資產,期望收益與標準差就是E(rp)=9%,σP=21%。如果選擇將全部投資投向無風險資產,期望收益與標準差就是E(rp)=3%,σP=0。從線上可直觀地看到,風險增加,收益也增加。由於直線的斜率為6/21=0.29,每增1單位風險,可獲0.29單位收益。即每增1單位收益,將增3.5(21/6=3.5)單位風險。








想知道,資本市場線和資本配置線有啥區別?