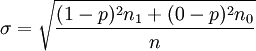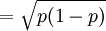離散指標

出自 MBA智库百科(https://wiki.mbalib.com/)

離散指標(Dispersion Index)

　　離散指標是用來測定總體各單位直接差異程度的統計指標，反應了變數值的離中趨勢。

　　離散指標有以下作用：

　　(1)是評價平均指標代表性的尺度。平均指標作為總體各單位標誌值一般水平的代表值，其代表性的高低取決於總體各單位標誌值的差異程度。一般來說，標誌值的分佈越分散，離散指標值越大，平均指標的代表性就越小；標誌值的分佈越集中，離散指標值越小，平均數的代表性就越大。

　　(2)離散指標是反映社會經濟活動過程均衡性的一個重要指標。一般來說，離散指標值愈小，則說明社會經濟活動過程愈均衡；離散指標值愈大，則說明社會經濟活動過程存在陡起陡落的現象，需要加以調控。

　　離散指標主要有全距、平均差、標準差和離散繫數。從數值的表現形式上看，分為絕對離中趨勢和相對離中趨勢。

　　1.反映絕對離中趨勢的指標

　　(1)全距(Range)

　　全距是總體各單位標誌值中最大值與最小值之差。一般以R表示全距。公式為：

　　對於組距數列，則全距：

　　R=最高組的上限-最低組的下限

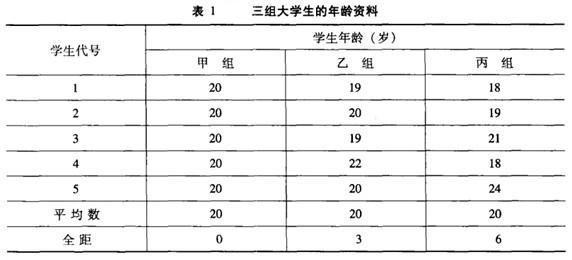
　　[例1]三組大學生的年齡資料如下：

　　計算結果表明三組大學生的平均年齡都為20歲，甲組全距為0，丙組全距最大，即說明甲組平均年齡代表性大，而丙組平均年齡代表陛較小。

　　全距的優點在於計算簡便，易於理解，可以反映變數值在一定範圍內的波動情況。缺點在於方法粗略，因為它只考慮兩端數值差異，沒有考慮中間數值差異的情況，也不受次數分配的影響，因而不能全面反映總體各單位標誌值的差異情況，準確性較差。要充分利用每一數據的信息，就需要利用平均差和標準差。

　　(2)平均差(AverageDeviation)

　　平均差是數列中各單位標誌值對其算術平均數之間絕對離差的平均數，它反映了數列中相互差異的標誌值的平均離散水平或差異程度。根據掌握的數據不同，平均差有簡單和加權兩種計量形式。

　　1)簡單平均差(SimpleAverageDeviation)。簡單平均差適用於未分組數據，其計算公式為：

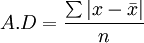
　　式中：A.D——平均差；

　　x——各變數值；

　　——算術平均數；

　　n——變數值的個數。

　　2)加權式平均差(WeightedAverageDeviation)。加權平均差適用於分組數據，其計算公式為：

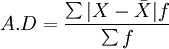
　　平均差的優點在於：由於它是根據全部標誌值與平均數絕對離差而計算出來的變異指標，因而能全面反映標誌值的差異程度。而且它沒有擴大和縮小離差，只是消除了離差的正負號。含義簡明，易於理解，顯然比全距精確得多。平均差的缺點在於：由於離差採用絕對值的形式，不考慮正負號，因此用這種方法計算得到的統計數值在性質上不是最優或最靈敏的，所以平均差在實際中應用較少，而被廣泛應用的是標準差。

　　(3)標準差(StandardDeviation)。

　　標準差，又稱均方差，是數列中各單位標誌值與其算術平均數離差平方和的算術平均數的平方根。標準差的平方稱為方差。與平均差比較，標準差是用平方的方法消除離差正、負號，因此用標準差測定標誌變動度比平均差更為合理，標準差是最常用、最重要的離散指標。根據掌握資料的不同，標準差也有簡單和加權兩種計量形式。

　　1)簡單標準差(SimpleStandardDeviation)。簡單標準差適用於未分組數據，其計算公式為：

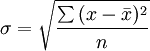
　　式中：σ——標準差(讀作西格瑪)；

　　x——變數值；

　　——變數值的算術平均數；

　　n——變數值的個數

　　2)加權標準差(WeightedStandardDeviation)。加權標準差適用於已分組數據，其計算公式為：

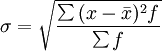
　　式中：f——變數數列中各組變數值所對應的次數。

　　標準差的優點在於：由於它能充分地利用每一個變數值提供的信息，因此，可以全面反映標誌值的差異程度；利用平方的方法解決正負號的問題，便於進一步的數學運算；經過開方和平方的過程，增強了極端值對變異測度值的影響。正因為標準差與全距和平均差相比有這麼多的優點，因而獲得了廣泛的應用。其中，常見的是用標準差來測定居民收入分配的差異程度、勞動生產率的差異程度及平均收支、平均分數、平均產量等經濟變數的代表性等等。

　　從上述平均差與標準差的計算，我們可以看出：

　　第一，平均差與標準差的大小不僅與離差情況有關，而且與變數值平均水平有關。如果變數值的平均水平越大，平均差與標準差就會越大；反之，則越小。所以，若兩個總體的均值不等，就不能用平均差或標準差比較變數值的離散程度及均值的代表性。例如，我們不能直接用外企人員的年平均收入與國企人員的年平均收入進行對比，說明哪一個群體的平均收入代表性高或離散程度大，因為這兩個群體的平均收人水平不同，不具有直接可比性。

　　第二，平均差與標準差受計量單位、研究現象的影響。這是由於平均差與標準差的計量單位為有名數，因而不同現象、不同單位的平均差或標準差都不能直接對比。例如，比較某一群體的平均身高和平均體重，問哪一個代表性高，就不能直接用平均差或標準差進行對比，因為這是兩種不同的現象，而且，計量單位也不同，前者用“米”，後者用“公斤”。 為瞭解決這些問題，於是就提出了相對離中趨勢指標的概念。

　　2.反映相對離中趨勢的指標

　　相對離中趨勢指標是用來反映總體分佈數列中標誌值離散程度的相對數指標，主要通過離散繫數進行測度。離散繫數又稱為變異繫數(CoefficientofVariation)，常用的相對離中趨勢的測度值有平均差繫數和標準差繫數。

　　(1)平均差繫數(CoefficientofAverageVariation)。平均差繫數是將簡單平均差及加權平均差分別除以相應的平均數，用以反映變數值離差的相對水平，它的計量單位為百分比，其計算公式為：

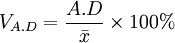
　　式中：V_A.D——平均差繫數；

　　A.D——簡單平均差或加權平均差；

　　——平均數。

　　(2)標準差繫數(CoefficientofStandardDeviation)。標準差繫數將簡單標準差及加權標準差分別除以相應的平均數，用以反映變數值離差的相對水平,它的計量單位為百分比。其計算公式為：

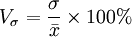
　　式中：V_σ——標準差繫數；

　　σ——簡單標準差或加權標準差；

　　——平均數。

　　3.反映交替標誌離中趨勢的指標

　　有些社會經濟現象的特征，只表現為兩種性質上的差異，例如，產品的質量表現為合格或不合格；對某一電視節目，觀眾表現為收看或不收看；農田按灌溉情況分為水澆田或旱田；等等，這些只表現為是或否、有或無的標誌稱為交替標誌，也稱作是非標誌。在進行抽樣估計時，交替標誌的標準差或方差有著重要意義。

　　(1)成數。總體中，交替標誌只有兩種表現，我們把具有某種表現或不具有某種表現的單位數占全部總體單位數的比重稱為成數。

　　(2)交替標誌的平均數。交替標誌表現了現象質的差別，因此計算其平均數首先需要將交替標誌的兩種表現進行量化處理。用“1”表示具有某種表現，用“O”表示不具有某種表現，這樣，我們就得到了是非標誌的分佈數列。

　　(3)交替標誌的標準差。根據前面所述標準差的計算方法，交替標誌的標準差是將變數值“1”、“0”分別減去其平均數“n”的離差平方的平均數再開方。即：