全球专业中文经管百科，由121,994位网友共同编写而成，共计436,015个条目

查看

工具▼

交替標誌

用手机看条目

出自 MBA智库百科(https://wiki.mbalib.com/)

交替標誌(Alternate Mark)

目錄

1 什麼是交替標誌[1]
2 交替標誌的平均數和標準差
- 2.1 交替標誌的平均數的內容[2]
- 2.2 交替標誌的標準差的內容[3]
3 參考文獻

什麼是交替標誌^[1]

　　在統計研究中，有時把被研究的社會經濟現象的全部單位，按是否具有某一標誌分為兩組。當標誌按“是否”或“有無”表示時，統計中叫交替標誌。它在總體單位間以兩種形式出現，非此即彼。交替標誌主要用於反映總體單位間性質上的差別。

交替標誌的平均數和標準差

　　交替標誌也可以計算平均數和標準差，在抽樣調查進行抽樣推斷時就需要這種計算。

交替標誌的平均數的內容^[2]

　　交替標誌平均數加權算術平均數不僅可以反映總體各單位數量標誌值的一般水平，還可以反映某些品質標誌的一般水平。在所研究的現象中，有許多品質標誌，它們在總體各單位只有屬性上的差異，無法直接計算其平均的屬性差異。統計實務中，常常是將此類現象各單位問的詹陛差異先數量化，然後再計算其算術平均數，以反映其質量的一般水平。

　　交替標誌又稱是非標誌。它是指總體中的各總體單位，某些單位具有某種屬性，而其他一些單位則不具有某種屬性。例如，一批產品中，一些是合格品，另一些是不合格品；一批種子，有些會發芽，另一些則不發芽。這些將總體單位劃為“是”或“否”、“有”或“無”兩類的標誌叫交替標誌。交替標誌只有質的差別，不能直接計算平均數，我們先將它們過渡到量的差異上來。以1作為具有某種屬性的單位標誌值，以0作為不具有某種屬性的單位標誌值，如上例中，我們就可以用1表示合格品的標誌值，0表示不合格品的標誌值。這樣就將交替標誌過渡到(0,1)的數量標誌了。

　　若全部總體單位數用N表示，其中具有某種屬性的總體單位數為 $N 1$ ，不具有某種屬性的總體單位數為 $N 2$ ，則

　　具有某種屬性的單位數所占比重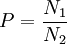 $P=\frac{N_1}{N_2}$ ；

　　不具有某種屬性的單位數所占比重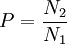 $P=\frac{N_2}{N_1}$ 。

　　可以證明P+Q=1

　　則可用比重權數公式計算交替標誌的平均數，公式為

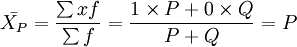
　　 $\bar{X_P}=\frac{\sum {xf}}{\sum f}=\frac{1\times P+0\times Q}{P+Q}=P$

　　例1

　　某廠去年生產的產品中，合格率為98％，通過表1，可計算該廠產品的平均合格率。

　　表1　　某場去年生產的產品平均合格率計算

	標誌值x	比重(%) 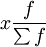$\frac{f}{\sum f}$	$x\frac{f}{\sum f}$
合格品	1	98	98
不合格品	0	2	0
合計	—	100	98

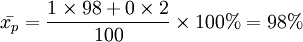
　　 $\bar{x_p}=\frac{1\times 98+0\times 2}{100}\times 100%=98%$

　　由此可見，該廠產品平均合格率為98％就是這批產品的合格率，也就是說，交替標誌的總體中，具有某種屬性的成數P就是這一總體(0,1)標誌的加權算術平均數。

交替標誌的標準差的內容^[3]

　　交替標誌的標準差，就是具有某一標誌值的單位在總體中的成數和不具有某一標誌值的單位在總體中的成數二者乘積的平方根。它反映了交替標誌的差異程度。其計算公式為：

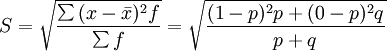
　　 $S=\sqrt{\frac{\sum {(x-\bar{x})^2f}}{\sum f}}=\sqrt{\frac{(1-p)^2p+(0-p)^2q}{p+q}}$

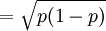
　　 $=\sqrt{p(1-p)}$

　　即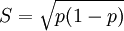 $S=\sqrt{p(1-p)}$

　　例2

　　在某縣31個鄉鎮抽取專業戶樣本296個中，有技術特長的有243戶，無技術特長的為53戶，其交替標誌的平均數和標準差如下：

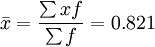
　　 $\bar{x}=\frac{\sum {xf}}{\sum f}=0.821$

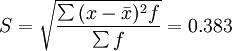
　　 $S=\sqrt{\frac{\sum {(x-\bar{x})^2f}}{\sum f}}=0.383$

　　　　　　　　　　表2 　　交替標誌平均數和標準差計算表

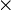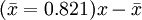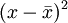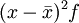
交替標誌值(變數)x	總體單位數(成數)f	變數 $\times$ 總體單位數xf	離差 $(\bar{x}=0.821)x-\bar{x}$	離差平方 $(x-\bar{x})^2$	離差平方加權 $(x-\bar{x})^2f$
1	0.821	0.821	0.179	0.032	0.026
0	0.179	0	0.821	0.674	0.121
合計	1	0.821	—	—	0.147

參考文獻

↑ 社會統計學第四章綜合指標第七節三、交替標誌的平均數與標準差.中國地質大學網路教育
↑ 謝啟南，韓兆洲主編.經濟學原理（第五版）.暨南大學出版社,2003.08
↑ 秦宗熙穆懷中等主編.人類社會研究法第1版.武漢大學出版社,1987.08

取自"https://wiki.mbalib.com/zh-tw/%E4%BA%A4%E6%9B%BF%E6%A0%87%E5%BF%97"

打开MBA智库App, 阅读完整内容打开App

如果您認為本條目還有待完善，需要補充新內容或修改錯誤內容，請編輯條目或投訴舉報。

本条目由以下用户参与贡献

Solitude1314,Yixi,方小莉.

頁面分類: 統計指標

評論(共0條)

提示:評論內容為網友針對條目"交替標誌"展開的討論，與本站觀點立場無關。

發表評論請文明上網，理性發言並遵守有關規定。

以上内容根据网友推荐自动排序生成

闽公网安备 35020302032707号