顯示性偏好理論
出自 MBA智库百科(https://wiki.mbalib.com/)
顯示性偏好理論(Revealed Preference Theory)、顯示偏好理論
目錄 |
顯示性偏好理論是由美國經濟學家保羅·薩默爾森(P.Samuelson)提出來的,其基本精神是:消費者在一定價格條件下的購買行為暴露了或顯示了他內在的偏好傾向。因此我們可以根據消費者的購買行為來推測消費者的偏好。這是一種不基於“偏好關係(效用函數)—消費者選擇”的邏輯思路,而是一個相反的過程,即“消費者選擇—偏好關係”。
該理論可以從消費者行為分辨最好的可能選擇。換句話說,消費者的消費習慣可以顯示他們的喜好。理論的出現,是基於消費者需求理論以邊際替代率作為依歸。而邊際替代率的假設,就是消費者是為了把功用極大化而作消費決定。雖然公用極大化的假設不受爭議,但需求理論隱含著的功用函數就難以被準確計算。顯示性偏好理論就能彌補需求理論的不足,借觀察行為來界定功用函數。
假設某甲有兩個消費選擇:買兩個蘋果和三條香蕉,或者買兩條香蕉和三個蘋果。如果兩個選擇的費用一樣,而他選了前者,那就表示某甲喜歡前者多於後者。然後,這顯示前者永遠都較後者受歡迎。如果該消費者買後者,就一定是他負擔不起買前者的費用。該理論進一步顯示,偏好是帶有傳遞關係的。如果我們有A、B、C 到 Z 多個選擇,而偏好 A 多於 B 、 B 多於 C ,如此類推。那結論就顯示出,我們對 A 的偏好多於 C ,一直數下去,多於 Z 。有了這套理論,經濟學家就可以規劃與消費者理論的模組一致的無差異曲線。
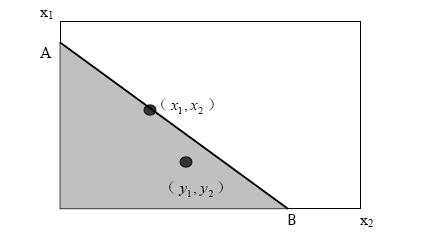
設消費者在價格為(p1,p2)時購買的商品束為(x1,x2),如果另一個商品組合(y1,y2)滿足如下條件:
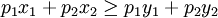 方程1
方程1
在這種情況下,若消費者總是在他能夠購買的商品束中選擇他最偏好的商品束,則一定有對(x1,x2)的偏好大於(y1,y2),即(x1,x2)是(y1,y2)的直接顯示偏好。
1.間接顯示性偏好
如果(x1,x2)是(y1,y2)的直接顯示偏好,同時(y1,y2)是(z1,z2)的直接顯示偏好,則(x1,x2)是(z1,z2)的間接顯示偏好。
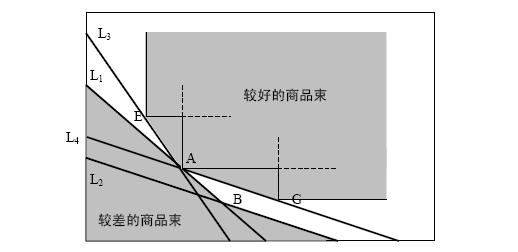
2.從顯示性偏好到無差異曲線
圖:無差異曲線的推導
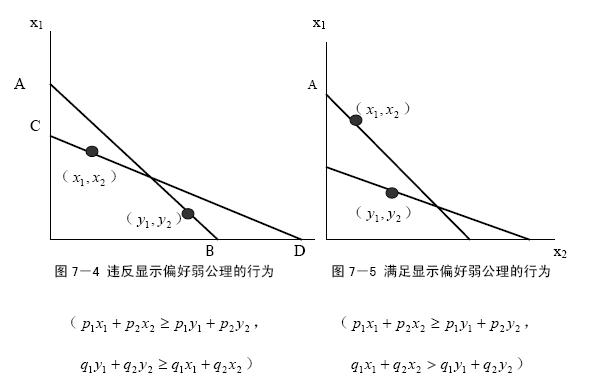
1.顯示偏好弱公理(WARP)的含義:
如果(x1,x2)直接顯示偏好於(y1,y2),且(x1,x2)和(y1,y2)是兩個不同的商品束,則(y1,y2)就不可能直接顯示偏好於(x1,x2)。
顯示偏好弱公理表明:若消費者在價格(p1,p1)下選擇(x1,x2),在價格(q1,q2)下選擇(y1,y2),只要:
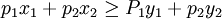 方程2
方程2
就不可能存在:
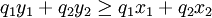 方程3
方程3
這意味著下式成立:
q1x1 + q2x2 > q1y1 + q2y2 方程4
2.WARP的圖示
3.WARP的檢驗:判斷消費者的行為是否符合WARP
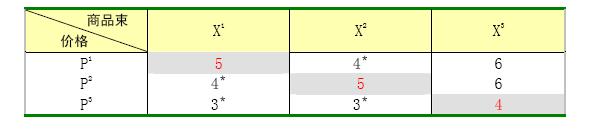
假設(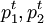 )表示第t期觀察到的價格,(
)表示第t期觀察到的價格,(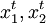 )表示第t期觀察到的消費者的選擇,若我們對一個消費者的消費行為觀察了3期,觀察值如表1所示:
)表示第t期觀察到的消費者的選擇,若我們對一個消費者的消費行為觀察了3期,觀察值如表1所示:
表1:消費者行為觀察值
根據以上的觀察值,我們可以判斷該消費者的行為是否符合WARP。我們首先計算消費者在不同價格水平下,購買不同商品束所需要支付的貨幣,結果如表2所示:
對角線上的各個數據為消費者在三個觀察期實際支出的費用,分別為:5,5,4。
在觀察期1(t=1),價格水平為p'=(1,2):消費者選擇的商品束為X1(支出的貨幣額為5),由於此時商品束X2也是消費者能買得起的商品束(需要支付的貨幣為4),但是消費者沒有購買,這表明商品束X1 > X2,即:
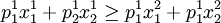 方程5
方程5
在觀察期2(t=2),價格水平變為p2 =(2,1),消費者選擇的商品束變為X2(支付的貨幣額為5),但是此時商品束X1也是消費者所能夠買得起的(需要支付的貨幣為4),而消費者沒有購買此商品束,即:
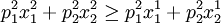 方程6
方程6
根據WARP可知,方程5和方程6不可能同時成立,因此該消費者的行為在X1與X2之間是不一致的,違背了WARP公理。
但是,該消費者在X3與X1及X2之間的,則沒有違背WARP公理。
顯示偏好強公理(SARP)是指如果(x1,x2)直接或間接顯示偏好於(y1,y2),且(x1,x2)和(y1,y2)是兩個不同的商品束,則(y1,y2)就不可能直接或間接顯示偏好於(x1,x2)。
顯示性偏好的探討[1]
從西方經濟學效用理論的發展中我們可以看到,序數效用論和顯示偏好理論是在否定基數效用論的基礎上發展起來的。從形式上看,這種否定確實避免了效用可以被直接計量這一令人困惑和尷尬的假設;但從內容上看,這種否定的有效性卻非常值得懷疑。序數效用論和顯示偏好理論對基數效用論的替代存在著明顯的邏輯缺陷,主要表現在以下兩個方面:
- 第一,序數效用論對基數效用論的替代是邏輯等價的同義反覆。
我們知道,在序數效用論中無差異曲線凸向原點是一個未經證明的假定,而序數效用論的其他結論、包括邊際替代率遞減規律和切點定律都是從這一前提中推導出來的。事實上,從常規思維出發,我們也能發現破綻,一個可以排序(不論按什麼標準)的事物卻不能通過數量來進行描述,是一件很荒唐的事。由此可見,離開了基數,任何序數都不能得到完整的說明。多年來,西方經濟學家仍不敢輕易拋棄基數效用論;才會出現我們前面提到的、在其他學科中絕無僅有的現象:兩種矛盾的理論竟可以如此相安無事地和平共處。
- 第二,顯示偏好理論是一個無法被經驗反駁和證偽的迴圈論證。
我們在前面曾經提到,拋開繁複的數學證明,顯示偏好理論無非要人們相信這樣一個結論:消費者在市場上選擇了某一消費品組合,他的偏好就同時被顯示了,因此經濟學家無需數量描述,就可以證明這一組合必然是效用最大化的。但是,用命題消費者選擇的消費品必然是效用最大化的來證明命題消費者選擇的是效用最大化的消費品,顯然是一個邏輯上的迴圈論證。因為顯示偏好理論事實上是用這樣一種方法來證明消費者的理性行為:某個消費品只要被消費者選擇了,那麼它肯定就是效用最大化的。這一結論沒有給經驗判斷留下絲毫反駁和證偽的餘地!按照這個邏輯來推論,消費者在任何情況下都是理性的:不抽煙是理性的,抽煙也是理性的;不酗酒是理性的,酗酒也是理性的;甚至吸毒和自殺都可以被視作一種理性行為,因為這些行為都是一個人根據自身偏好最大化作出的選擇。
批判理性主義哲學的創始人波普爾在批判弗洛伊德精神分析法的偽科學性質時曾經舉過一個例子:任何可以想到的病例和行為都能用弗洛伊德的理論加以解釋,例如,一個人為了淹死一個小孩而把他推入水中,另一個人為了拯救一個小孩而犧牲了自己的生命;按照弗洛伊德的理論,第一個人是因為戀母情結受到了壓抑,第二個人是因為戀母情結得到了升華。波普爾說,一種在任何情況下都適用(儘管不排除在某些情況下它的確適用)並且總是得到證實的理論不可能是科學的理論,判別一種理論是否科學的標準不是它的可證實性,而是它的可證偽性;換言之,科學的理論不能一勞永逸地在肯定的意義上被選拔出來,而只能在否定的意義上藉助經驗檢驗被選拔出來。
在波普爾看來,一個經驗的科學體系必須可以被經驗所反駁,那些可以解釋一切的理論,正是由於它們不可能被經驗證偽而失去了作為科學理論的資格。特別值得指出的是,波普爾認為數學命題不是科學,因為它們與邏輯重言式一樣均屬於同義反覆,且邏輯永真而不能被證偽!,因而不屬於科學命題的範疇。
顯示偏好理論把效用最大化能不能定量分析這樣一個實證性的經驗命題演繹成一個純粹的數學命題,不但沒有解決基數效用論與序數效用論之間的矛盾,反而因企圖迴避這一矛盾使自己陷入了更大的邏輯困境。
- ↑ 葉航. 西方經濟學效用範式的邏輯缺陷[J]. 經濟學家, 2003, 000(001):93-97.
評論(共20條)
如果(x1,x2)是(y1,y2)的直接顯示偏好,同時(y1,y2)是(z1,z2)的直接顯示偏好,則(x1,x2)是(z1,z2)的直接顯示偏好。
請專家講解一下 在這裡為什麼(x1, x2) 不是 (z1, z2) 的間接顯示偏好??
如果(x1,x2)是(y1,y2)的直接顯示偏好,同時(y1,y2)是(z1,z2)的直接顯示偏好,則(x1,x2)是(z1,z2)的直接顯示偏好。
請專家講解一下 在這裡為什麼(x1, x2) 不是 (z1, z2) 的間接顯示偏好??
由於前期編輯失誤,應為間接顯示偏好,而非直接顯示偏好。已將錯誤之處修正。
請問“買2個蘋果和3個香蕉”和“買3個香蕉和2個蘋果”不是一模一樣嗎?是否第二個為“3個蘋果和2個香蕉”
是的 我也看到了 應該是你說的這樣
性 // 行
謝謝指正,已修改~










感謝講解