支付矩陣
出自 MBA智库百科(https://wiki.mbalib.com/)
支付矩陣(Payoff table/ Payoff matrix)或稱報酬矩陣、收益矩陣、贏得矩陣、得益矩陣
目錄 |
支付矩陣是指在博弈論中,用來描述兩個人或多個參與人的策略和支付的矩陣。不同參與人的利潤或效用就是支付。
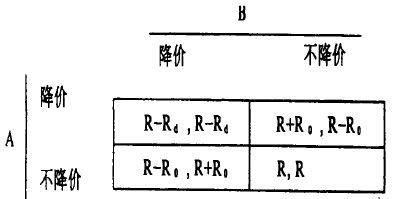
在價格戰中,企業和競爭者之間是一種非合作博弈關係。在博弈過程中,企業和競爭者都有兩種策略選擇:降價和不降價。假定在某一產業中形成了寡頭市場結構,有兩個企業A和B生產同一類產品。他們共同分享同一市場,在降價前各自獲得的收益相等均為R;當採取價格戰時,一個企業認為先通過降價可以獲得較高的市場份額,由此可使得收益增加為Ro,相對於另一個企業不降價因此而損失Ro的收益:如果另一個企業也同樣採取降價策略,那麼面對既定的市場,兩個企業會因價格下降而帶來損失,損失都為Rd(且Rd<Ro)。這樣就形成了下表的博弈支付矩陣:
通過比較支付矩陣參數的收益支付水平可以看出:在給定A企業時,B企業選擇降價策略都比不降價策略好,也就是說降價策略是B的最優策略:同樣給定B企業的策略時,A的最優策略也是降價策略。於是(降價,降價)構成了一個博弈的納什均衡(R-Rt, R-Rd),也就是相應的均衡收益。
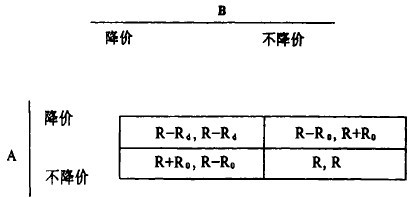
繼續採用上面的假設,現在來分析下麵情況,既然雙方降價與誰都無利,那麼當一個降價,另一個不降價而採用其他價格競爭策略(比如搞好售後服務等)時,會出現不同情況,由於採用某種策略適應了社會需求,受到消費者的普遍贊同,從而吸引了大量的顧客,會產生新的收益分配的格局,形成了下麵的支付矩陣:
該支付矩陣儘管是將表一中右上角和左下角對調,但卻有著不同的經濟含義和博弈後果。同樣可以得到:不管B採取降價與不降價策略,A都會採取不降價策略:而對於B而言,也會是同樣的抉擇。因此,(不降價,不降價)變成了該支付矩陣的納什均衡。這樣,雙方達成了一種默契和共識——合作。
通過上面的分析不難看出,採取合作的態度比起雙方採用降價競爭的策略有利多了,顯然是一種較為良性的狀態。但它並非是理想的均衡狀態,如果僅僅是維持現狀,滿足現存的收益水平,那麼整個行業乃至社會將不思進取,也將不會有經濟社會的繁榮。








為什麼我算出來“合作”是製造商的占優策略呢?難道是我看表計算錯了?(X,Y)X是