戰略博弈

出自 MBA智库百科(https://wiki.mbalib.com/)

　　戰略博弈是指一種相互作用決策的棋型，這種模型假定每個決策主體選擇且僅選擇一次行動計劃，並且這些選擇是同時進行的。該模型包括參與人的有限集合N，對每個參與人i有一個行動集合A_i和一個建立在行動組合上的偏好關係。我們稱一個行動組合a=a_j(j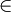N）為結果，並且用A表示結果集合X_j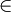NA_j。這裡要求將每個參與人i的偏好定義在A而不是A_i上，這是將戰略博弈從決策問題中區分出來的特征所在，即每個參與人不僅要考慮自己的行動，還要考慮其他參與人採取的行動。

　　一個戰略博弈包括:

　　有限集合N(參與人集合)

　　對每個參與人i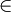N有一非空集A_i(對參與人i有效的行動集合）。

　　對每個參與人i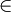N，一個建立在集合A=X_jA_j(j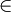N)上的偏好關係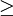i(參與人i的偏好關係)。

　　如果每個參與人i的行動集合A_i是有限的，則博弈是有限的。

　　該模型如此抽象使其能應用於較廣的情形範圍。一個參與人可以是單獨的一個人或任何一個決策主體如政府、董事會、革命運動中的領導集體，甚至可以是一朵花或一隻動物。該模型沒有限制參與人有效的行動集合，例如，它可以包含幾個元素或是一個具有多種狀態依存的複雜計劃集合。然而，由於我們要求一個參與人只對應一個偏好關係，該模型的使用範圍也因此而有限。參與人偏好關係可以只是簡單地反映參與人對可能結果的感受，在一個有機體不能有意識活動的情形下它可以是繁殖成功的機會。

　　該模型如此抽象的事實，有利於它應用於很廣的範圍，但同時也有缺陷，因為模型的內涵不依賴於情形的任何特有性質。實際上，在這個抽象程度上，對於博弈的結果得不出什麼結論。要得到有趣的結論，模型應更加具體化。

　　在一些情形下，參與人的偏好非常自然地被定義在結果上而不是行動組合本身。例如，當要對寡頭壟斷建模時，我們可能將公司集合作為參與人集合，將價格集合作為每個公司的行動集合;但我們可能希望對這樣的假設建模，即每個公司僅關心她的利潤，而不關心產生利潤的價格組合。為此，就要引進一個結果集合C;一個函數g：A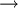C，它將結果與行動組合聯繫起來，以及一個C上的偏好關係組合(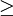i ^* )。那麼在戰略博弈中每個參與人的偏好關係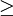i被定義為：a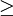ib，當且僅當g(a)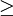i ^* g(b)。

　　有時我們希望對這樣一種情形建模，即行動組合結果受外來的一個隨機變數的影響，而參與人在行動前並不知道這種影響能否實現。對此我們也能作為戰略博弈處理：引進一個結果集合C，概率空間Ω和一個函數g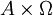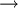：C。該函數的解釋是：當行動組合是a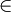A隨機變數的實現值是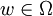，則g(a,w)便是結果。行動組合包括C上一個不確定事件(lottery）對每個參與人i，偏好關係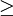i ^* 必須是在所有這些不確定事件集合上的具體化。在戰略博弈中參與人i的偏好關係定義如下:a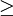ib，當且僅當根據關係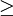i ^* ，C上被g(a,*)起的不確定事件至少與被g(b,*)引起的不確定事件具有相同的後果。

　　在一個廣泛的範圍里，戰略博弈中參與人i的偏好關係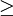i，可以用支付函徽u_i：A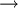R(亦稱為效用函數)來表示，該函數的意義是，只要a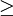ib,就有u_i(a)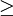u_i(b)。我們稱這一函數值為支付(或效用)。我們經常通過給定一個支付函數來確定一參與人的偏好關係。就此而言我們將博弈表示成<N(A_i),(u_i)>，而不是<N，A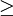_i,(i)>。

　　具有兩個參與人的有限戰略博弈可由圖1中的表便利地表示。用行表示一個參與人的行動，另一個參與人的行動則用列表示。由行r和列c形成的方框中的兩個數，為行參與人選擇r和列參與人選擇c時兩人的支付。這樣在表1的博弈中，行參與人的行動集合為|T,B|，列參與人的行動集合為|L,R|，並且從結果(T，L)來看，行參與人的支付為w₁，列參與人的支付為w₂。若參與人的名字為“1”和“2”，則可以方便地說行參與人為參與人1，列參與人為參與人2。表1兩個參與人戰略博弈的便利表示，假定每個參與人有兩種行動：

	L	R
T	（w1,w2）	（x1,x2）
B	（y1,y2)	（z1,z2）

　　戰略博弈的一般解釋是:這是一個事件只發生一次的模型。每一個參與人都知道博弈的細節及所有參與人都是“理性的”事實;並且參與人同時獨立地選擇他們的行動。在這種解釋下每個參與人在選擇他的行動時並不知道別的參與人的選擇，沒有信息〔除模型的基本元素外)可以讓參與人用來形成對別人行動的預期。

　　另一個解釋是：參與人可以通過此種博弈或在過去進行的相似博弈的信息來形成別的參與人的行為預期。只要博弈行動間不存在戰略聯繫，則博弈行動系列都可用戰略博弈來建模。也就是，一個多次從事博弈的人必須只關心他此刻的支付而忽略他現在的行動對其他參與人將來行動的影響。在這種解釋下只要排除相互作用事件間的非暫時戰略聯繫，那麼將情形模化成戰略博弈便是恰當的。

　　當稱戰略博弈參與人行動為“同時的”時候，我們並不強調這些行動是在時間的同一點上完成。如下的一種情形也能用戰略博弈來建模:參與人在終點前處子不同位置，開始參與人的可能行動和支付是公開說明瞭的(這樣它們便是參與人間的共同知識)，然後每個參與人通過向中央電腦輸入一條信息來選擇一個行動，當所有信息被收到後參與人便知道他們的支付了。不過，戰略博弈模型應用範圍比這個例子所提供的還要廣泛得多。應用戰略博弈建模的重要之處在於，參與人獨立作決策且所有參與人在做決策前並不知道其他參與人的選擇。