平均發展水平
出自 MBA智库百科(https://wiki.mbalib.com/)
平均發展水平(Average level of development)
目錄 |
平均發展水平又稱“序時平均數”、“動態平均數”,是時間序列中各項發展水平的平均數,反映現象在一段時期中發展的一般水平。
序時平均數作為一種平均數,與靜態平均數有相同點,即它們都抽象了現象的個別差異,以反映現象總體的一般水平。但二者又有明顯的區別,主要表現在:序時平均數抽象的是現象在不同時間上的數量差異,因而它能夠從動態上說明現象在一定時期內發展變化的一般趨勢;靜態平均數抽象的是總體各單位某一數量標誌值在同一時間上的差異,因此,它是從靜態上說明現象總體各單位的一般水平。由於不同時間序列中觀察值的表現形式不同,序時平均數有不同的計算方法。
(一)絕對數時間數列的序時平均數
絕對數時間數列序時平均數的計算方法是最基本的,它是計算相對數或平均數時間數列序時平均數的基礎。絕對數時間數列有時期數列和時點數列之分,序時平均數的計算方法也有所區別。
1、時期數列的序時平均數,其計算公式為:
 (1)
(1)
式中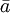 為序時平均數,n為觀察值的個數。
為序時平均數,n為觀察值的個數。
例1:對錶1中的國內生產總值序列,計算年度平均國內生產總值。
表1 中國國內生產總值等時間序列表
| 年份 | 國內生產總值(億元) | 第三產業占GDP比重(%) | 年底總人口(萬人) | 職工平均貨幣工資(元) |
|---|---|---|---|---|
| 1990 1991 1992 1993 1994 1995 1996 1997 1998 1999 | 18547.9 21617.9 26638.1 34634.4 46759.4 58478.1 67884.6 74462.6 78345.2 81910.9 | 31.3 33.4 34.3 32.7 31.9 30.7 30.1 30.9 32.1 33.0 | 114333 115823 117171 118517 119850 121121 122889 123626 124810 125909 | 2140 2340 2711 3371 4538 5500 6210 6470 7479 8346 |
資料來源:《中國統計年鑒》,中國統計出版社,2001年
解:根據時期數列序時平均數公式有:
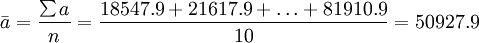 (億元)
(億元)
2、由時點數列計算序時平均數。在社會經濟統計中一般是將一天看作一個時點,即以“一天”作為最小時間單位。這樣時點數列可認為有連續時點和間斷時點數列之分;而間斷時點數列又有間隔相等與間隔不等之別。其序時平均數的計算方法略有不同,分述如下:
1)連續時點數列計算序時平均數。在統計中,對於逐日排列的時點資料,視其為連續時點資料。這樣的連續時點數列,其序時平均數公式可按公式(1)計算,即
 (2)
(2)
例如,存款(貸款)平均餘額指標,通常就是由報告期內每日存款(貸款)餘額之和除以報告期日曆數而求得。
另一種情形是,資料登記的時間單位仍然是1天,但實際上只在指標值發生變動時才記錄一次。此時需採用加權算術平均數的方法計算序時平均數,權數是每一指標值的持續天數。
計算公式如下:
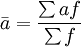
例2:某種商品5月份的庫存量記錄如表2,計算5月份平均日庫存量。
表2 某種商品5月份庫存資料
| 日期 | 1-4 | 5-10 | 11–20 | 21-26 | 27-31 |
|---|---|---|---|---|---|
| 庫存量(台) | 50 | 55 | 40 | 35 | 30 |
解:該商品5月份平均日庫存量為
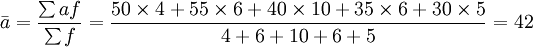 (台)
(台)
2)間斷時點數列計算序時平均數。實際統計工作中,很多現象並不是逐日對其時點數據進行統計,而是隔一段時間(如一月、一季度、一年等)對其期末時點數據進行登記。這樣得到的時點數列稱為間斷時點數列。如果每隔相同的時間登記一次,所得數列稱為間隔相等的間斷時點數列;如果每兩次登記時間的間隔不盡相同,所得數列稱為間隔不等的間斷時點數列。
當其時點資料是以月度、季度、年度為時間間隔單位,我們已不可能像連續時點資料那樣求得準確的時點平均數。這種情況下,我們可以根據資料所屬時間的間隔特點,選用不同的計算公式。對於間隔相等的資料,採用“首末折半”;對於間隔不等的資料,採用“間隔加權”的方法計算序時平均數。
例3:某商業企業1999年第二季度某種商品的庫存量如表3,試求該商品第二季度月平均庫存量。
表3 某商業企業1999年第二季度某商品庫存量
| 3月末 | 4月末 | 5月末 | 6月末 | |
|---|---|---|---|---|
| 庫存量(百件) | 66 | 72 | 64 | 68 |
- 解:4月份平均庫存量=
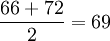 (百件)
(百件)
- 5月份平均庫存量=
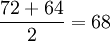 (百件)
(百件)
- 6月份平均庫存量=
 (百件)
(百件)
- 第二季度平均庫存量
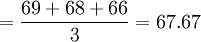 (百件)
(百件)
為簡化計算過程,上述計算步驟可表示為:
第二季度平均庫存量=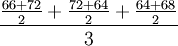 =
=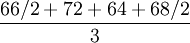 =67.67(百件)
=67.67(百件)
根據上述計算過程可推導出計算公式為:
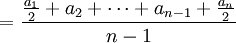 (4)
(4)
該公式形式上表現為首末兩項觀察值折半,故稱為“首末折半法”。這種方法適用於間隔相等的間斷時點數列求序時平均數。
例4:表4列示了我國1990~1999年年末人口的部分年份資料,計算年平均人口數。
表4 中國1990-1999年部分年份年末人口數
| 年份 | 1990 | 1992 | 1995 | 1998 | 1999 |
|---|---|---|---|---|---|
| 年底總人口(萬人) | 114333 | 117171 | 121121 | 124810 | 125909 |
解:對資料進行觀察分析,屬間隔不等的間斷時點資料,採用“間隔加權”方法。
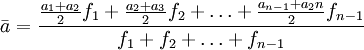 (5)
(5)
- =120355.33(萬人)
(二)相對數或平均數時間數列的序時平均數
相對數和平均數是兩個有聯繫的相對數對比求得,用符號表示即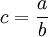 。因此,由相對數或平均數數列計算序時平均數,不能直接根據該相對數或平均數數列中各項觀察值簡單平均計算(即不應當用
。因此,由相對數或平均數數列計算序時平均數,不能直接根據該相對數或平均數數列中各項觀察值簡單平均計算(即不應當用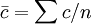 的公式),而應當先分別計算構成該相對數或平均數數列的分子數列和分母數列的序時平均數,再對比求得。用公式表示為:
的公式),而應當先分別計算構成該相對數或平均數數列的分子數列和分母數列的序時平均數,再對比求得。用公式表示為:
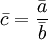 (6)
(6)
例5:某企業1999年第四季度職工人數資料如表5,計算工人占職工人數的平均比重。
表5 某企業1999年四季度職工人數資料
| 9月末 | 10月末 | 11月末 | 12月末 | |
| 工人人數/人 職工人數/人 工人占職工比重/% | 342 448 76.34 | 355 456 77.85 | 358 469 76.33 | 364 474 76.79 |
解:


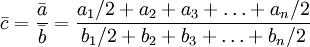
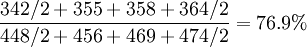








比較全面,可以推薦