終值
出自 MBA智库百科(https://wiki.mbalib.com/)
終值(future value)
目錄 |
終值又稱將來值或本利和,是指現在一定量的資金在將來某個時點上的價值。
在日常生活中有許多屬於終值計算的問題。例如,張先生最近購買彩票,中獎100000元,他想將這筆錢存入銀行,以便將來退休時抵用,設張先生還有10年退休,如按年存款利率2%計算,10年後張先生退休時能拿多少錢?
- (一)單利的計算
設現有一筆資金,共計金額為P,存期為n年,年利率為i,則n年後的終值FVn為:
FVn=P+P·i·n=P(1+i·n)
上例中,張先生退休能拿的本利和為100000×(1+2%×10)=120000元。
- (二)複利的計算
設現有一筆資金,共計金額為P,存期為n年,年利率為i,則n年後的終值FVn為:
第1年年末的本利和為P(1+i)
第2年年末的本利和為P(1 + i) + P(1 + i)i = P(1 + i)2
第3年年末的本利和為P(1 + i)2 + P(1 + i)2i = P(1 + i)3
……
第n年年末的本利和為P(1 + i)n
因此,FVn = P(1 + i)n
式中,(1 + i)n在財務管理學上稱為複利終值繫數,我們用FVIFi,n表示,它是計算複利終值的主要參數。其中i是計算貨幣價值的利息率,n是貨幣到期長度。人們可以用專門的程式在電子電腦中計算出來,以避免手工計算麻煩。
上例中,如果按複利計算,則張先生10年後退休可獲得
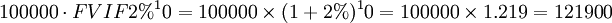 元。
元。
評論(共4條)
在下雖然數學方面極不善,敢問上文中以下公式是否有誤呢?
“第2年年末的本利和為P(1 + i) + P(1 + i)i = P(1 + i)2”
“第3年年末的本利和為P(1 + i)2 + P(1 + i)2i = P(1 + i)3”
中間的P(1 + i)i,利率的平方?實在不明。 ----- Umbrella Revolution
這個公式應該是本利和為 P(1 + i) + P(1 + i)i = P(1 + i)(1 + i)=P(1 + i)^2,求出則得出利率的平方,公式沒有錯誤呀
在下雖然數學方面極不善,敢問上文中以下公式是否有誤呢?
“第2年年末的本利和為P(1 + i) + P(1 + i)i = P(1 + i)2”
“第3年年末的本利和為P(1 + i)2 + P(1 + i)2i = P(1 + i)3”
中間的P(1 + i)i,利率的平方?實在不明。 ----- Umbrella Revolution
其實第二年就是等於第一年 X (1+i) 也就是第一年 P (1 + i) 第二年 P (1 + i) (1 + 1) = P (1 + i )^2
在下雖然數學方面極不善,敢問上文中以下公式是否有誤呢?
“第2年年末的本利和為P(1 + i) + P(1 + i)i = P(1 + i)2”
“第3年年末的本利和為P(1 + i)2 + P(1 + i)2i = P(1 + i)3”
中間的P(1 + i)i,利率的平方?實在不明。 ----- Umbrella Revolution
哈哈哈哈,你的數學確實極為不善








在下雖然數學方面極不善,敢問上文中以下公式是否有誤呢?
“第2年年末的本利和為P(1 + i) + P(1 + i)i = P(1 + i)2”
“第3年年末的本利和為P(1 + i)2 + P(1 + i)2i = P(1 + i)3”
中間的P(1 + i)i,利率的平方?實在不明。 ----- Umbrella Revolution