過程能力指數
出自 MBA智库百科(https://wiki.mbalib.com/)
過程能力指數(Process capability index,CP或CPK),也譯為工序能力指數、工藝能力指數、製程能力指數
目錄 |
過程能力指數也稱工序能力指數,是指工序在一定時間里,處於控制狀態(穩定狀態)下的實際加工能力。它是工序固有的能力,或者說它是工序保證質量的能力。這裡所指的工序,是指操作者、機器、原材料、工藝方法和生產環境等五個基本質量因素綜合作用的過程,也就是產品質量的生產過程。產品質量就是工序中的各個質量因素所起作用的綜合表現。對於任何生產過程,產品質量總是分散地存在著。若工序能力越高,則產品質量特性值的分散就會越小;若工序能力越低,則產品質量特性值的分散就會越大。那麼,應當用一個什麼樣的量,來描述生產過程所造成的總分散呢?通常,都用6σ(即μ+3σ)來表示工序能力:
工序能力=6σ 若用符號P來表示工序能力,則: P=6σ 式中:σ是處於穩定狀態下的工序的標準偏差
工序能力是表示生產過程客觀存在著分散的一個參數。但是這個參數能否滿足產品的技術要求,僅從它本身還難以看出。因此,還需要另一個參數來反映工序能力滿足產品技術要求(公差、規格等質量標準)的程度。這個參數就叫做工序能力指數。它是技術要求和工序能力的比值,即
工序能力指數=技術要求/工序能力 Cp=T/6σ T——公差 σ——[[總體標準差]](或用樣本標準差S)
當分佈中心與公差中心重合時,工序能力指數記為Cp。當分佈中心與公差中心有偏離時,工序能力指數記為Cpk。運用工序能力指數,可以幫助我們掌握生產過程的質量水平。
製程能力是過程性能的允許最大變化範圍與過程的正常偏差的比值。
製程能力研究在於確認這些特性符合規格的程度,以保證製程成品不符規格的不良率在要求的水準之上,作為製程持續改善的依據。
當我們的產品通過了GageR&R的測試之後,我們即可開始Cpk值的測試。
CPK值越大表示品質越佳。
CPK=min((X-LSL/3s),(USL-X/3s))
CPK= Min[ (USL- Mu)/3s, (Mu - LSL)/3s]
過程能力指數運算有5種計算方法:
- 直方圖(兩種繪圖方法);
- 計算剩餘標準差;
- 排列圖(自動檢索和排序);
- 波動圖(單邊控制規範,也可以是雙邊控制規範)。
1.過程能力指數Cp、Cpk
我們常常提到的過程能力指數Cp、Cpk是指過程的短期能力。
Cp是指過程滿足技術要求的能力,常用客戶滿意的偏差範圍除以六倍的西格瑪的結果來表示。
Cp=(允許最大值-允許最小值)/(6*σ)
所以σ越小,其Cp值越大,則過程技術能力越好。
Cpk是指過程平均值與產品標準規格發生偏移的大小,常用客戶滿意的上限偏差值減去平均值和平均值減去下限偏差值中數值小的一個,再除以三倍的西格瑪的結果來表示。
Cpk=MIN(允許最大值-過程平均值,過程平均值-允許最小值)/(3*σ)
2.過程能力指數Pp、Ppk
與Cp、Cpk不同的是, 過程能力指數Pp、Ppk是相對長期的過程能力,要求其樣本容量大,
其公式同Cp、Cpk一樣,但σ是全部樣本的標準偏差,即等於所有樣本的標準差S。
同Cpk息息相關的兩個參數:Ca , Cp.
Cpk = Cp * ( 1 - |Ca|)
Cpk是Ca及Cp兩者的中和反應,Ca反應的是位置關係(集中趨勢),Cp反應的是散佈關係(離散趨勢)
1 當選擇製程站別Cpk來作管控時,應以成本做考量的首要因素,還有是其品質特性對後製程的影響度。
2. 計算取樣數據至少應有20~25組數據,方具有一定代表性。
3. 計算Cpk除收集取樣數據外,還應知曉該品質特性的規格上下限(USL,LSL),才可順利計算其值。
4. 首先可用Excel的“STDEV”函數自動計算所取樣數據的標準差(σ),再計算出規格公差(T),及規格中心值(u). 規格公差=規格上限-規格下限;規格中心值=(規格上限+規格下限)/2;
5. 依據公式:Ca=(X-U)/(T/2) , 計算出製程準確度:Ca值 (x為所有取樣數據的平均值)
6. 依據公式:Cp =T/6σ , 計算出製程精密度:Cp值
7. 依據公式:Cpk=Cp(1-|Ca|) , 計算出製程能力指數:Cpk值
8. Cpk的評級標準:(可據此標準對計算出之製程能力指數做相應對策)
A++級 Cpk≥2.0 特優 可考慮成本的降低
A+ 級 2.0 > Cpk ≥ 1.67 優 應當保持之
A 級 1.67 > Cpk ≥ 1.33 良 能力良好,狀態穩定,但應儘力提升為A+級
B 級 1.33 > Cpk ≥ 1.0 一般 狀態一般,製程因素稍有變異即有產生不良的危險,應利用各種資源及方法將其提升為 A級
C 級 1.0 > Cpk ≥ 0.67 差 製程不良較多,必須提升其能力
D 級 0.67 > Cpk 不可接受 其能力太差,應考慮重新整改設計製程。
過程能力指數的值越大,表明產品的離散程度相對於技術標準的公差範圍越小,因而過程能力就越高;過程能力指數的值越小,表明產品的離散程度相對公差範圍越大,因而過程能力就越低。因此,可以從過程能力指數的數值大小來判斷能力的高低。從經濟和質量兩方面的要求來看,過程能力指數值並非越大越好,而應在一個適當的範圍內取值。
過程能力指數案例分析[1]
服務是一種無形的產品,對其如何進行質量控制呢?在工業質量管理的方法里,有一種指標叫做過程能力指標Cpk,表示生產的部件與設計界限規定的範圍的吻合程度,我們發現,把它應用在服務業上,也是一種很好的控制方法。下麵就以某銀行為例子,來說明它的應用。
某銀行在營業高峰期時,顧客的等待時間最少是4分鐘,銀行承諾最多11分鐘要辦理完其全部業務,這是銀行對過去的業務經驗的總結,同時認為,一般的平均等待時間是8分鐘,這反映了其職員處理業務的平均速度和平均熟練程度。在某個高峰時段銀行辦理了50位客戶業務,每位客戶的等待時間如下(為了便於計算0.5表示半分鐘):
9.5,6.0,8.0,8.5,10.5,8.5,10.0,9.0,6.0,9.5,8.0,8.5,7.5
9.0,8.5,10.0,7.5,9.0,6.5,9.5,8.0,8.5,10.0,7.0,7.0,9.5,8.5,9.0,8.0,8.0,11.0,7.5,8.5,6.5,10.5,8.0,7.0,9.0,8.5
9.0,8.0,8.0,6.5,7.5,8.5,8.5,7.0,7.5,9.0,9.0
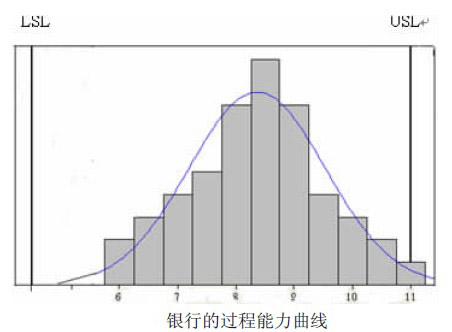
從這些數據可以看出銀行實現了對顧客的承諾,每位顧客的等待時間都不超過11分鐘,是否可以說該銀行的服務質量達到了標準?部門經理應該如何評價本銀行的的業務處理能力呢?
首先,我們要對這些數據作分析處理,如上圖。從圖中我們可以得到,直方圖表示數據的頻度,數據的分佈大體上是服從正態分佈的,且曲線中值偏向右側。
USL和LSL分別表示的是服務要求範圍的上限和下限,在本案例中就是11分鐘和4分鐘,即落在這個界限內的顧客等待時間都是合適的。一般對於USL和LSL的獲得,可以有兩種方法。一是固有的標準,例如,某鋼板厚度控制在6.4到5.6毫米為合格品,這就是標準;另外一個是以往的經驗的總結,例如根據某種經驗,處理某些業務,根據正常的程式,一般要3到8天等等。
使用統計軟體可以計算出樣本數據的平均值和標準差分別是8.36和1.165,我們用與S來表示,在數學上它們分別是與a的無偏估計值。接下來讓我們看一下它們的現實意義。
平均值=8.36分,反映了曲線的位置,是位置參數。這個數字對於顧客來說,它反映了在該銀行辦理業務的平均等待時間;對該銀行來說,他反映了該部門的平均效率;而對於其職員來說,它反映了職員辦理業務的平均熟練程度。
而標準差S反映了顧客等待時間,即銀行服務速度的波動性,波動造成差異,這是服務質量變異的屬性。差異的擴大會造成失控,在失控狀態下,可能會造成業務的阻礙和客戶的不滿與抱怨。因此,對於S當然是越小越好,因為它越小表示數據越集中,越靠近平均值,也就是時間長度的差異不大;如果S越大,就表示變化範圍越大,也就是差異很大,很可能會造成服務質量變異。
顧客等待的標準差S=1.165分,它的意義就是:在平均值的正負三個S的分鐘里,即從4.5分鐘到12分鐘,大約有99.73%顧客等待的時間在這個界限範圍內。
有了這些數據,我們可以用過程能力指數Cpk進行評價。
過程能力指數Cpk原來指企業生產合格品能力的大小,在本案例中Cpk指銀行對顧客履行承諾的能力大小。通常將Cpk分為五個等級,以便針對不同的情況採取不同的措施來改進質量。特級:Cpk > 1.67,這時服務能力過高,企業可以考慮放寬質量要求;一級:1.33 < Cpk < 1.67,那就是服務能很好地滿足標準,是一種理想的狀態;二級:1.00 < Cpk < 1.33,可以認為服務質量是正常的,企業應該加強服務質量的控制和提高,以達到理想的狀態;三級:0.67 < Cpk < 1.00,服務質量較差,企業應該採取措施,加強對服務提供質量的控制與管理;四級:Cpk < 0.67,企業服務質量嚴重不足,需要改進,如果Cpk越小,那麼服務很可能已經嚴重失控。
Cpk的計算公式如下:
![C_{pk}=\min\left[\frac{USL-\mu}{3\sigma}-\frac{\mu-LSL}{3\sigma}\right]](/w/images/math/3/f/7/3f786472b104f0b7542c2784e8a719c5.png)
帶入本案例數據計算出Cpk為0.76,該企業服務質量處於第三級,從管理層面來講,表示服務質量不足,應立即採取措施改善。如果遇到這種情況,我們應該如何解決呢?管理者可以把曲線儘量向規定的中心位置移動。本案例中,一般顧客的平均等待時間是8分鐘,可以說這是根據以往經驗得到的平均效率,是正常的程式運作可以達到的,而顧客實際上平均的等待時間是8.36分,偏離了0.36。因而質量曲線表現出向右偏移的現象,這樣就會導致偏移出規定的範圍。所以,我們應該儘量把平均時間向中心位置(8分)靠近,即縮短顧客等待時間。產生顧客等待現象的根本原因是服務現場的抵達者數量超過系統的處理能力,因此,減少等待時間的最好方案是消除根本原因,這通常需要對現有的生產和人力資源策略進行重新考察。由於這樣的改變可能需要花錢,所以商業銀行管理人員必須高度重視服務質量和顧客滿意度,把費用與提供給顧客更快服務的競爭優勢聯繫起來。
- 鑒於此,我們擬將對減少顧客等待時間的策略淺述如下
- (一)加強員工培訓,規範工作程式
管理者可以通過加強對員工的培訓與監督,特別是效績較差的員工,來改進服務質量,同時管理者應該建立一套規範的工作程式,使服務過程標準化,並且制定遇到特殊情況時的處理方式,以免顧客流失。此外,銀行可向顧客提供“如何減少等待時間”宣傳手冊,提醒顧客高峰期的時間,並鼓勵他們在不擁擠的非高峰時間尋求服務,那個時候服務會更快、更舒適。
- (二)切實推行隨機動態服務系統,實現服務時間的最優配置
一般情形下,商業銀行提高服務水平自然就會降低顧客等待費用,但卻常常增加了服務機構的成本。為解決這個問題,有必要切實推行隨機動態服務系統,最大限度縮短顧客等待時間,使商業銀行的服務時間達到最優配置。其中要重點考慮和解決以下兩個方面的內容:(1)性態問題。指各種顧客排隊系統的概率規律性,研究隊伍長度分佈、等待時間分佈和高峰期顧客分佈等;(2)服務系統的統計推算。即判斷一個給定的排隊系統符合哪種模型,服從於哪種統計分佈規律。
- (三)改進視窗設置方式和採取叫號方法
銀行營業廳需要改進服務視窗設置方式,即不應全部設置為綜合視窗和讓顧客不加區別地排隊,而是應根據顧客類別(如根據顧客辦理業務種類不同分為現金業務、非現金業務、理財業務等,根據顧客辦理業務額大小分為大額業務和小額業務等)分設不同服務視窗和讓不同顧客分別排在不同價置。其次,採取號碼排隊結構,即顧客到達銀行營業廳後,通過號票印表機獲得號碼,當叫到自己所持號碼時即到服務台接受服務。此種排隊結構有效地減少了顧客的體力成本和精神成本,能夠保證“先到先服務”,顧客隱私和安全得到最大程度保障,從而受到顧客極大歡迎。
- (四)創新服務手段,提高服務效率
信息技術的飛速發展使銀行逐漸改變了以櫃面服務為主的營業方式,而側重於服務體系的建設,以低成木高效率的“機構+滑鼠”的方式發展,以實體銀行的信譽、信用和基本功能為平臺,延伸虛擬網點,從而收到“1+1>2”的效果。例如擴展自助設備功能,方便服務一般客戶。自助設備相對於櫃面服務來說,操作簡單快捷,是服務一般客戶口常存取款、代繳費等業務的主要手段,並且能有效減輕櫃面的人流壓力,使需要辦理複雜業務的客戶能更快地得到服務。利用互聯網技術開通網上銀行服務,不僅降低了的運營成本,還剋服了時間和空間上的障礙,使顧客金融交易和服務可在任何時間、任何地點進行。
管理者結合上述手段,通過具體的措施實現改進,縮短顧客的等待時間,提高服務效率。當部門可以穩定達到指標時,管理者可以調節LSL與USL的值或中心值,例如,管理者可以把USL的值調到10分鐘,計算得Cpk為0.47,顯然降低,管理者需要進一步加強措施來提高效率。通過這樣不斷的調節,可以使服務標準得到不斷改進與提高,並且在實際操作上加以配合,才可以達到顧客所意想不到的高效率與滿意度。同時這是一種以數據和現實分析驅動的管理方法,它可以應用到很多地方,例如,餐飲、物流、零售等服務業,幫助我們改進和提高服務質量。
測量誤差對過程能力指數的影響[2]
任一製造過程的輸出值(零件的特性值)都要通過一個測量系統獲得測量數據,很多統計學 家與質量管理專家長期的實踐與研究得出,測量數據X是由零件的基準值Xp和測量誤差ε兩部分疊加而成的,即:
X = Xp + ε (1)
這就是測量數據的結構式。對式(1)兩邊求方差,可得:
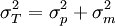 (2)
(2)
式中,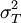 為測量數據的總方差;
為測量數據的總方差;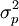 為零件間的方差;
為零件間的方差;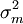 為測量系統的方差。
為測量系統的方差。
真實的過程能力指數應該是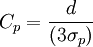 ,
但在存在測量誤差時計算的過程能力指數為
,
但在存在測量誤差時計算的過程能力指數為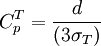 ,兩者存在如下關係式:
,兩者存在如下關係式:
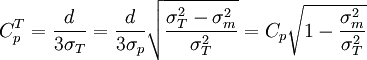 (3)
(3)
在測量系統經過標定,其分辨力、穩定性和線性已經達到可接受水平時,測量系統的方差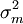 只由重覆性方差
只由重覆性方差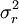 和再現性方差
和再現性方差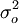 兩部分組成,這樣,測量系統的總方差由3部分組成,即:
兩部分組成,這樣,測量系統的總方差由3部分組成,即:
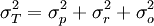 (4)
(4)
令TV = 5.15σT,PV = 5.15σp,EV = 5.15σr,AV = 5.15σo則由式(4)得到:
(TV)2 = (PV)2 + (EV)2 + (AV)2 (5)
TV為總變差,式(5)稱為總變差平方的分解式,其中後兩項的平方和(EV)2 + (AV)2稱為量具重覆性和再現性(記為R&R)的平方,R&R是表徵測量系統好壞的特征數,它越小越好,它在總變差中所占百分比記為%R&R ,即:
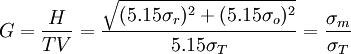 (6)
(6)
- 註:G為%R&R,H為R&R
將式(6)代人式(3) ,可得:
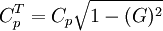 (7)
(7)
- 註:G為%R&R
因此在存在測量誤差時,過程能力指數 較之真實的過程能力指數Cp偏低,從而會低估過程能力。
較之真實的過程能力指數Cp偏低,從而會低估過程能力。
為了減少測量誤差對過程能力指數的影響,必須對測量系統的能力進行評價。當測量過程處於穩定狀態時,在一定時間內選定標準件反覆測量其標準樣品,以測量值做控製圖,考察其穩定性。若測量過程處於穩態,可以利用極差法估計重覆性標準差σr和再現性標準差σo,進而計算評價標準R&R來評價測量系統的能力是否滿足要求。
評論(共28條)
CPK值越大表示品質越佳。
CPK=min((X-LSL/3s),(USL-X/3s)) wrong
具體怎麼錯,期待您的完善,MBA智庫是可以自由編輯的,您也可以直接參与修改
CPK= Min[ (USL- Mu)/3s, (Mu - LSL)/3s] 中間為什麼要用逗號隔開啊
逗號隔開表示:CPK等於上公差的Cp和下公差的Cp里較小的那一個 。
示例說明:
min[a,b]表示的意思是取數字a與b中的較小者,即:
min[a,b]=a,當a<b時;
min[a,b]=b,當b<a時
CPK= Min[ (USL- Mu)/3s, (Mu - LSL)/3s] 中間為什麼要用逗號隔開啊
這個符號的意思就是取最小的一個,CPK是取CPL或CPU中較小的一個
過程能力指數只有Cp定義是正確的,而且是科學的,它源自質量大師1950年代的“能力比”(後改稱過程能力指數),這也是朱蘭大師對質量管理科學的一個貢獻。但是Cp僅僅是對稱公差在質量特性值均值剛好落在目標值M時的過程能力指數計算公式,發生偏移時過程能力指數計算公式是什麼?公差不對稱時過程能力指數計算公式又應該是什麼?單側公差要求時過程能力指數計算公式是什麼?這是一個數學問題。這個問題自20世紀80年代成為國際質量界探討的熱門話題。因為MBA教材上所列的這些公式,有一個算一個,都是錯誤的。這個問題已經被中國來自企業的科學家宋祥彥攻剋,他因此可以稱為質量管理專家,從數學公式應用於質量管理科學的角度講,他也可以稱為質量管理數學家。
為什麼要取min而不取max。
銀行適用這個嗎?我覺得從顧客角度說應該是越接近0越好啊?就算都是8又有什麼意義?
顧客的角度當然是時間越短越好了,但這樣的前提是銀行得花人力和資金的大投入,生意人講究的是做生意,是賺錢,又不是做慈善。銀行也要賺錢吧。你去超市花還想花2塊怡寶的錢買瓶脈動嗎?
講那麼多純理論的東西幹嗎,我只要會用就行,麻煩給出一個電腦計算的公式,並說明其中的每一項的意義和作用,謝謝!
1、公式計算的應用背後是基礎理論的研究與論證 2、百科中的內容是面向所有人的
銀行適用這個嗎?我覺得從顧客角度說應該是越接近0越好啊?就算都是8又有什麼意義?
正解
樣本數都在標準範圍內,為什麼計算出來的CPK還是那麼低,都是0點幾
1.離散程度看看,數據是否呈正態分佈的,假如標準偏差很大,CPK同樣很小。2.看一下μ值多少,如果偏倚過大,CP就算很好,CPK也會很差的
CPK值越大表示品質越佳。
CPK=min((X-LSL/3s),(USL-X/3s)) wrong
放屁,你學號再發表評論好吧,CPK值越大表示品質越佳 但CPK的取值公式人家沒寫錯
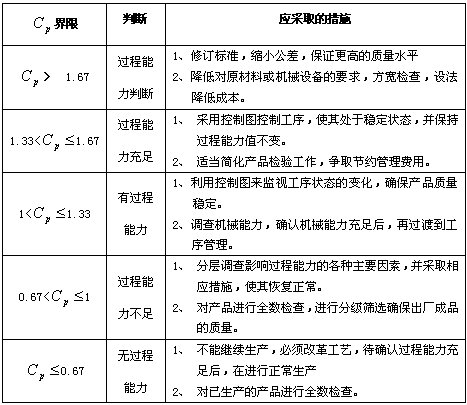








那個過程能力的判斷的圖好像有一些小錯誤啊。