幾何平均收益率
用手机看条目
出自 MBA智库百科(https://wiki.mbalib.com/)
幾何平均收益率(The geometric average rate of return)
目錄 |
[編輯]
幾何平均收益率是將各個單個期間的收益率乘積，然後開n次方。幾何平均收益率使用了複利的思想，即考慮了資金的時間價值，也就是說，期初投資1元，第一期末則值(1 + R1)元，第二期投資者會將(1 + R1)進行再投資，到第二期末價值則為(1 + R1)(1 + R2)元，……。
這個平均收益指標優於算術平均收益率，因為它引入了複利的程式，即通過對時間進行加權來衡量最初投資價值的複合增值率，從而剋服了算術平均收益率有時會出現的上偏傾向。
[編輯]
如果Rij表示資產組合j的第i個可能的收益率，且每一結果的可能性相同，那麼該資產組合的幾何平均收益率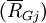
為：
![\overline{R}_{Gj} = [(1+R_{1j})^{\frac{1}{N}}(1+R_{2j})^{\frac{1}{N}}...(1+R_{Nj})^{\frac{1}{N}}-1.0]](/w/images/math/d/0/b/d0be9615a5ead41f94f76049e54137bc.png)
如果每個觀察值的可能性不同，Pij是第i個收益率的概率，那麼幾何平均收益率為：
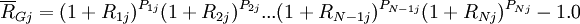
用符號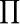
表示乘積，上式可寫為：
[編輯]
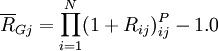
例如，某種股票的市場價格在第1年年初時為100元，到了年底股票價格上漲至200元，但時隔1年，在第2年年末它又跌回到了100元。假定這期間公司沒有派發過股息，這樣，第1年的投資收益率為100％[R1＝（200-100）/100=1=100%]，第2年的投資收益率則為-50%[R2= (100-200)/200=-0.5＝－50％]。
實際上，投資者儘管進行了兩年的股票投資，但他的實際財富情況並未發生任何變化，其凈收益為零。採用幾何平均收益率來計算，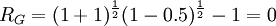
。這個計算結果符合實際情況，即兩年來平均收益率為零。
[編輯]
RG計算的這個公式錯了！！！