算術平均收益率
用手机看条目
出自 MBA智库百科(https://wiki.mbalib.com/)
目錄 |
[編輯]
算術平均收益率是最簡單的方法，即算術平均收益率(R)是將各單個期間的收益率(R)加總，然後除以期間數(n)，計算公式如下：
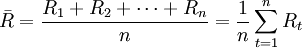
算術平均收益率還假定，投資者通過追加或提取資金的方法始終將最初的投資金額保持不變。值得指出的是：當各期收益出現巨大波動時，算術平均收益率會呈明顯的上偏傾向。算術平均數法適用於各期收益率差別不大的情況，如果各期收益率差別很大的話，這樣計算出來的收益率會歪曲投資的結果。
[編輯]
例如，某種股票的市場價格在第1年年初時為100元，到了年底股票價格上漲至200元，但時隔1年，在第2年年末它又跌回到了100元。假定這期間公司沒有派發過股息，這樣，第1年的投資收益率為100％（R1＝（200-100）/100=1=100%），第2年的投資收益率則為－50%(R2= (100-200)/200=-0.5＝－50％)。
用算術平均收益率來計算，這兩年的平均收益率為25％，即：R=[100%+(-50%)] /2=25%。而實際上，在整個投資期間，投資者並未賺到任何凈收益。
[編輯]
請問為什麼波動大的時候算術平均收益率會有向上的偏差