算术平均收益率

出自 MBA智库百科(https://wiki.mbalib.com/)

　　算术平均收益率是最简单的方法，即算术平均收益率(R)是将各单个期间的收益率(R)加总，然后除以期间数(n)，计算公式如下：

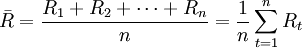
　　算术平均收益率还假定，投资者通过追加或提取资金的方法始终将最初的投资金额保持不变。值得指出的是：当各期收益出现巨大波动时，算术平均收益率会呈明显的上偏倾向。算术平均数法适用于各期收益率差别不大的情况，如果各期收益率差别很大的话，这样计算出来的收益率会歪曲投资的结果。

　　例如，某种股票的市场价格在第1年年初时为100元，到了年底股票价格上涨至200元，但时隔1年，在第2年年末它又跌回到了100元。假定这期间公司没有派发过股息，这样，第1年的投资收益率为100％（R₁＝（200-100）/100=1=100%），第2年的投资收益率则为－50%(R₂= (100-200)/200=-0.5＝－50％)。

　　用算术平均收益率来计算，这两年的平均收益率为25％，即：R=[100%+(-50%)] /2=25%。而实际上，在整个投资期间，投资者并未赚到任何净收益。

• 平均收益率
• 几何平均收益率
• 时间加权收益率
• 实际收益率
• 期望收益率