货币先行模型

出自 MBA智库百科(https://wiki.mbalib.com/)

货币先行模型（Cash in advance model或CIA model）

　　当代西方宏观经济学中另一广泛使用的是货币先行(cash in advance或CIA)模型。该模型由克拉奥(Clower，1967)首先提出，其前提是消费必须用货币来购买。从技术上讲，这相当于给模型增加了一个现金约束。克拉奥之后，大卫·斯托克曼(David Stockman，1981)发展了不仅消费品而且投资品也要用货币来购买的模型，罗伯特·卢卡斯（Robert E.Lucas）和斯道克曼(1983，1987)此后又将消费品分为必须用现金购买(现金物品)和可用信贷购买(信贷物品)的两部分。CIA模型的优点在于它在保持动态最优分析的同时可以很容易地推导出货币需求。

　　该模型前提是消费必须使用货币来购买。为了达到这一目的，克拉奥在模型中假设了一个货币在先约束，即物品购买量受先前换取的货币量的约束。这是人们预算约束之外的另一约束。它隐含着两种限制：其一，货币为购买物品的唯一媒介；其二，货币必须在物品交换之前换取。Clower之后，Stockman发展了不仅消费品而且投资品也要用货币来购买的模型。

不考虑不确定性，代表性行为人的目标函数可写作：

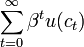　　 (1)

式中，β为贴现率，效用函数u(·)为连续可微、严格递增的凹函数。行为人通过消费和资产选择使目标函数极大化。为简单起见，下面我们不考虑资本，假定债券是除货币外的惟一金融资产。以名义量表示的该极大化问题的约束条件为：

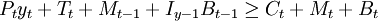　　 (2)

式中，T_t为来自于政府的净转移收入，B_{t − 1}是行为人在t—1期持有的t期到期的债券，I_{t − 1}是t—1到t期的名义债券收益，其他变量的含义相同。用t期物价水平去除上式，得到以实际量表示的约束：

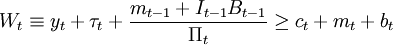　　 (3)

式中，τ_t = T_t / P_t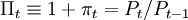，，行为人在 t+1期的全部资源为：

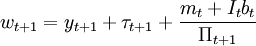　　 (4)

除了上述限制之外，CIA模型增加了1个货币先行约束：

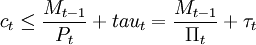　　 (5)

即t期的消费支出不能超过持有至t期的实际货币余额加期初得到的转移支付。由于持有货币存在放弃利率的机会成本，因此等式(5)通常取等号。

　　t期的选择变量为c_T,M_T和B_t。由于行为人的消费既受资源限制也受现金约束，t期状态可以用行为人所拥有的资源w和持有的现金m_{t − 1}表示。

令值函数

　　V(w_t,m_{t − 1}) = maxu(c_t) + βV(w_{t + 1},m_t) (6)

则该值函数的极值约束于等式(3)、(4)和(5)。

令债券的实际收益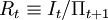，并且由等式(3)可知b_t = w_t − c_t − m_t，将这些关系代人等式(4)，我们得到

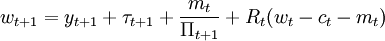
利用w_{t + 1}这一表达式，令μ为与等式(5)相关的拉格郎日乘数，行为人的消费和货币持有量的一阶条件为：

　　u_c(c_t) − βR_tV_w(w_{t + 1},m_t) − μ_t = 0 (7)

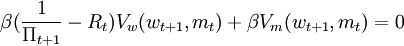　　 (8)

根据包络定理：

　　V_w(w_t,m_{t − 1}) = βR_tV_w(w_{t + 1},m_t) (9)

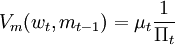　　 (10)

令λ_t，为时期t财富的边际价值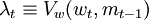：，根据等式(9)，等式(7)可写作：

　　u_c(c_t) = λ_t + μ_t (11)

即消费的边际效用等于财富的边际效用(λ_t)加货币提供的服务价值(μ_t)。由于消费品必须用货币来购买，因此与MIU模型相比，消费成本增加了货币提供的服务成本，行为人使消费的边际效用等于该成本加财富的边际效用。

　　CIA模型表明，如果货币供给为一常量，那么货币在该模型中就具有正价值，这是因为货币能减少货币在先这一约束条件的影子成本。CIA模型的优点在于它保持动态最优分析的同时可以很容易地推导出货币需求。CIA模型与MIU模型一样，它们并不专门讨论为什么货币具有如此特别的功能。但与MIU模型不一样的是，CIA模型中关于货币的正价值并不依赖于任何关于消费和真实货币量在效用函数中的可分离性，这就让模型摆脱了一个不必要的束缚。

　　CIA模型也说明了稳态的货币值为正和货币的超中性等问题。由于存在货币先行限制，实际消费等于实际货币余额，稳态通胀率等于名义货币存量增长率。然而，基本的CIA模型不能说明通胀的福利成本和最优通货膨胀率问题，根据这一模型，预期通胀不会影响货币需求，这一结论显然不太现实。克拉奥之后，库勒和阿尔文·汉森(Cooley and Alvin·Hansen，1989)将消费品进一步区分为现金物品和信贷物品，从而得以使消费与所持货币量之比随预期通胀变动。