茎叶图

出自 MBA智库百科(https://wiki.mbalib.com/)

茎叶图（Stem and leaf plot）

　　茎叶图又称“枝叶图”，它的思路是将数组中的数按位数进行比较，将数的大小基本不变或变化不大的位作为一个主干（茎），将变化大的位的数作为分枝（叶），列在主干的后面，这样就可以清楚地看到每个主干后面的几个数，每个数具体是多少。

　　茎叶图有三列数：左边的一列数统计数，它是上（或下）向中心累积的值，中心的数（带括号）表示最多数组的个数；中间的一列表示茎，也就是变化不大的位数；右边的是数组中的变化位，它是按照一定的间隔将数组中的每个变化的数一一列出来，象一条枝上抽出的叶子一样，所以人们形象地叫它茎叶图。

　　茎叶图是一个与直方图相类似的特殊工具，但又与直方图不同，茎叶图保留原始资料的资讯，直方图则失去原始资料的讯息。将茎叶图茎和叶逆时针方向旋转9O度，实际上就是一个直方图，可以从中统计出次数，计算出各数据段的频率或百分比。从而可以看出分布是否与正态分布或单峰偏态分布逼近。

　　茎叶图在质量管理上用途与直方图差不多，但它通常是作为更细致的分析阶段使用。由于它是用数字组成直方图，所以在做的时候比直方图时，通常我们常使用专业的软件进行绘制。

　　1、用茎叶图表示数据有两个优点：一是从统计图上没有原始数据信息的损失，所有数据信息都可以从茎叶图中得到；二是茎叶图中的数据可以随时记录，随时添加，方便记录与表示。

　　2、茎叶图只便于表示两位有效数字的数据，而且茎叶图只方便记录两组的数据，两个以上的数据虽然能够记录，但是没有表示两个记录那么直观、清晰。

　　茎叶图是将统计分组和次数分配一次完成，是探索性数据分析中对数据的初步形象描绘。其图形直观且保留原始信息，均值、中位数和众数均可依原始数据准确方便地算出。现以某班一次考试成绩为例，介绍茎叶图的作法。

　　作图过程是先作“茎”后填“叶”，将分组标志(组距)视为茎，按数的大小从上到下(也可从下到上)排列。将每一个观察值视为一个树叶，每一个树叶按照树茎之要求长在应长的树茎上。对于百分制的考试分数，先将高位数字按顺序排成一列，后将每个分数的个位数为叶长在相应的茎上，最后将每茎上的叶按从大到小的排列。若人数较多，树叶较长，可将高位数重复两次，个位数分为0～5一枝，5～9一枝。图1即为最后完成的茎叶图表。为了便于分析，可将1/4、3/4分位数及中位数用符号标出。

　　利用茎叶图对考试成绩进行评估

　　1、班级内成绩评估

　　1）将茎叶图茎和叶逆时针方向旋转9O度，实际上就是一个班级成绩带有数字的直方图，可以从中统计出次数，计算出各分数段的频率或百分比，从它可以看出班级成绩的分布是否与正态分布或单峰偏态分布逼近。

　　2）若茎叶图成绩表扁而宽(如图1)，说明该班整体成绩较集中，成绩差异不大；如果茎叶图长而窄，说明该班成绩较分散，标准差较大，高分低分差距大。这可使教师或校管理部门对学生成绩有所了解。

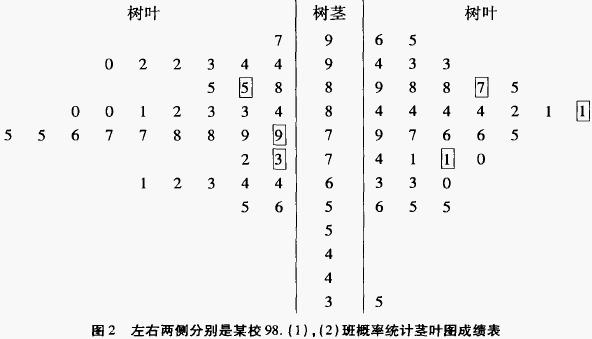
　　3）异常成绩的发现及处置。茎叶图成绩表中若有少数成绩远离中位数，如图2中右侧，说明这类学生与一般学生有质的区别，对于优秀的学生应加以培养，对于差的学生应找出根源加以帮助。这些异常值在计算标准差时可剔除，如图2右侧，x=77.1，标准差σ = 12.6，剔除异常值后，x=78.3，σ = 10.8，这样可更科学地反映平均成绩。

　　4)科学反映学生在班级中的名次。茎叶图成绩表中的成绩被带有方框的字分成4个区域，依次代表四个不同的水平，各层次学生都占总数的25％ 。例如，图2对应的某一学生考了75分，在右侧的二班是中等水平，而在左侧的一班只属下等水平，这样比较避免了以绝对分数来判定学生的成绩。

　　2、班级间学生的评估

　　要对平行班同一课程的成绩比较，可将两个班的成绩作为叶长在同一茎上，分别自左右两侧扩张，如图2对照起来，简明多了。若要对多个班级成绩进行比较，可将茎叶垂直方向平行移动，作为茎叶图。先将茎叶图看成直方图观察两班成绩整体分布状况。若两班成绩图形均接近正态分布且中位数接近，说明两班的成绩差别不大；若两侧的峰值相距较远，中位数差别大，说明两班总体成绩相差较大。

　　1）若对同一教师任教的平行班茎叶图表进行比较，先看1/4，3/4分位数和中位数，如果两个班的中位数较接近，说明其成绩没有显著性差异，如果中位数接近，而茎叶图的形状有较大差异，从总体上来看成绩差异不大，但图形长而窄的班级两极分化较大，教学难度大。如果中位数差别较大，则说明两个班级学生的基础，学习风气有较大差异。对不同教师平行班比较时，中位数高的班级整体水平较高。

　　2）计算出左右两侧的H一散布，即1/4位数与3/4位数的差。图(2)中左H一散布为10分，右H一散布为16分，由此看到左侧中等水平的学生成绩差距并不大，竞争激烈，而右图中的中等水平之间差距较大，教学有一定的难度。

　　3、结论

　　茎叶图法是数理统计中数据分析的一种方法，将它应用到成绩评估中，可保留原始分数，对学生成绩作出科学化评价。其特点是做法简单，评价全面，为教师和教学管理部门提供了一种教学质量评估的方法。