贴现现金流量法
出自 MBA智库百科(https://wiki.mbalib.com/)
贴现现金流量法(拉巴波特模型,Rappaport Model,DCF法)
目录 |
贴现现金流量法是由美国西北大学阿尔弗雷德·拉巴波特于1986年提出,也被称作拉巴波特模型(Rappaport Model),是用贴现现金流量方法确定最高可接受的并购价值的方法,这就需要估计由并购引起的期望的增量现金流量和贴现率(或资本成本),即企业进行新投资,市场所要求的最低的可接受的报酬率。
该模型所用的现金流量是指自由现金流量(Free Cash Flow,简写FCF)即扣除税收、必要的资本性支出和营运资本增加后,能够支付给所有的清偿者的现金流量。
用贴现现金流量法评估目标企业价值的总体思路是:估计兼并后增加的现金流量和用于计算这些现金流量现值的折现率,然后计算出这些增加的现金流量的现值,这就是兼并方所愿意支付的最高价格。如果实际成交价格高于这个价格,则不但不会给兼并企业带来好处,反而会引起亏损。
运用贴现现金流量法的步骤[1]
运用贴现现金流量法需经过三个步骤:
第一步,建立自由现金流量预测模型。
拉巴波特认为有五种价值动因影响目标企业的价值,即销售增长率、经济利润边际、新增固定资产投资、新增营运资本、边际税率等。他把这五种因素运用在自由现金流量模型中,公式表述为:
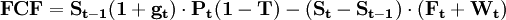
其中:
- FCF——自由现金流量;
- St——年销售额;
- gt——销售额年增长率;
- Pt——销售利润率;
- T——所得税率;
- Ft——销售额每增加1元所需追加的固定资本投资;
- Wt——销售每增加1元所需追加的营运资本投资;
- t——预测期内某一年度。
第二步,估计折现率或加权平均资本成本。
折现率是考虑了投资风险后,兼并方要求的最低收益率,也就是该项投资的资本成本。这里所指的资本成本不是并购方企业自身的加权资本成本,而是并购方投资于目标企业的资本的边际成本。由于并购方用于并购的资金来源是复杂的,可能来自留存收益、增发新股,也可能是举债融资,这就需要对各种各样的长期资本成本要素进行估计,并计算加权平均资本成本。其中,自有资金的成本可用资本资产定价模式求得,而债务成本则可用债务利息经税务调整后的有效资本成本得到。最后,该项投资的资本成本就是这二者的加权平均,也就是平均资本成本(K),即:
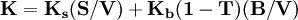
其中:
第三步,利用贴现现金流量模型,计算现金流量的现值。
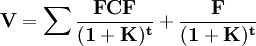
其中,
贴现现金流量法以现金流量预测为基础,充分考虑了目标公司未来创造现金流量能力对其价值的影响,在日益崇尚"现金至尊"的现代理财环境中,对企业并购决策具有现实的指导意义。但是,这一方法的运用对决策条件与能力的要求较高,且易受预测人员主观意识(乐观或悲观)的影响。所以,合理预测未来现金流量以及选择贴现率(加权平均资本成本)的困难与不确定性可能影响贴现现金流量法的准确性。
现金流量折现法是资本投资和资本预算的基本模型,被看作是企业价值评估模型中在理论上最为成熟的模型。因为企业的经济活动主要表现为现金的流入和流出,由于其有坚实的理论基础,当与其他方案一起使用时,现金流量折现法所得出的结果往往成为检验其他模型结果合理与否的基本标准。
现金流量折现法的原理比较简单,它是通过权衡为收购而投入的现金量与这一投资未来所能产生的所有净现金量(扣除折旧、营运需要等)和时间来计算的。通过这一模型还可以计算得出投资方案本身的内部收益率(IRR),即现金流入量现值等于现金流出量现值时所得到的内含报酬率。
现金流量折现法的主要缺点是其对现金流量估计和预测的固有的不确定性。在现实生活中,几乎每个企业都会存在着随生命周期的起伏而经历不同的成长阶段:企业早期的成长率高于整个经济体系成长率;企业中期的成长率等于经济体系成长率;而企业晚期的成长率明显低于整个经济体系成长率。再加上由于必须考虑诸如有关市场、产品、定价、竞争、管理、经济状况、利率、汇率等相关因素,准确性因而减弱。由于它注意到了可能存在的最重要的假定和不确定性因素,尤其是将它用于为买方确定最高定价时,其结果往往具有重要的参考价值,因此在并购中应该推广使用现金流量折现法。[1]
贴现现金流量法的案例[2]
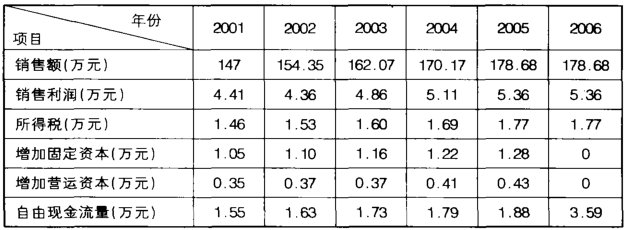
假如A公司拟在2001年初收购目标企业B公司。经测算收购后有6年的自由现金流量,2000年B公司的销售额为140万元,收购前5年的销售额每年增长5%,第六年的销售额保持第五年的水平,销售利润率(含税)为3%,固定资本增长率和营运资本增长率分别为15%和5%,加权平均资本成本为1O%,求目标企业的价值。依据上述资料,计处其结果见下表:
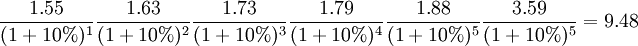 (万元)
(万元)
由此可见,如果A公司能够以9.48万元或更低价格购买B公司,那么这一并购活动从价格上讲将是合理的。
总之,贴现现金流量法以现金流量预测为基础,充分考虑了目标公司未来创造现多流量能力对其价值的影响,在日益崇尚的现代理财环境中,对企业并购决策具有现实的指导意义。








好资料,谢啦!