利率平价理论
出自 MBA智库百科(https://wiki.mbalib.com/)
利率平价理论 （Interest Rate Parity Theory）
目录 |
利率平价理论 （Interest Rate Parity Theory）认为两个国家利率的差额相等于远期兑换率及现货兑换率之间的差额。由凯恩斯和爱因齐格提出的远期汇率决定理论。他们认为均衡汇率是通过国际抛补套利所引起的外汇交易形成的。在两国利率存在差异的情况下，资金将从低利率国流向高利率国以谋取利润。但套利者在比较金融资产的收益率时，不仅考虑两种资产利率所提供的收益率，还要考虑两种资产由于汇率变动所产生的收益变动，即外汇风险。套利者往往将套利与掉期业务相结合，以避免汇率风险，保证无亏损之虑。大量掉期外汇交易的结果是，低利率国货币的现汇汇率下浮，期汇汇率上浮；高利率国货币的现汇汇率上浮，期汇汇率下浮。远期差价为期汇汇率与现汇汇率的差额，由此低利率国货币就会出现远期升水，高利率国货币则会出现远期贴水。随着抛补套利的不断进行，远期差价就会不断加大，直到两种资产所提供的收益率完全相等，这时抛补套利活动就会停止，远期差价正好等于两国利差，即利率平价成立。[1]因此我们可以归纳一下利率平价说的基本观点：远期差价是由两国利率差异决定的，并且高利率国货币在期汇市场上必定贴水，低利率国货币在期汇市场上必定升水。
利率平价理论核心观点[2]
通过利率同即期汇率与远期汇率之间的关系来说明汇率的决定与变动的原因。该学说认为远期差价是由两国利差决定的，（远期汇率的升水、贴水率约等于两国间的利率差异）并且高利率货币在远期市场上必定贴水，低利率货币在远期市场上必为升水，在没有交易成本（transaction cost）的情况下，远期差价等于两国利差，即利率平价（interest parity）成立。
利率平价理论的基本内容[3]
利率平价理论可分为无抛补利率平价（Uncovered Interest Rate Parity, UIRP）和抛补的利率平价（Covered Interest Rate Parity, CIRP）两种。此两者的不同之处在于对投资者的风险偏好所做的假定上。
对于投资者按风险分类：风险厌恶者需要获得一定的风险报酬才愿意持有风险资产；与此相反，风险爱好者愿意获得承担风险的权利，但其会付出一定代价；而风险中立者则愿意在没有风险收益的情况下承担风险。
（一）无抛补利率平价
定义：在资本具有充分国际流动性的条件下，投资者的套利行为使得国际金融市场上以不同货币计价的相似资产的收益率趋于一致，也就是说，套利资本的跨国流动保证了“一价定律”适用于国际金融市场。
决定机制：
利率的变化取决于无风险条件下投资者的投机决策，即
（1）在年终若持有单位本币的存款与收益额大于持有外币存款与收益额按预期汇率 折算成的本币款，即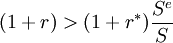
，则在本国存款；
（2）在年终若持有单位本币的存款与收益额小于持有外币存款与收益额按预期汇率 折算成的本币款，即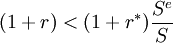
，则在外国存款；
（3）在年终若持有单位本币的存款与收益额等于持有外币存款与收益额按预期汇率 折算成的本币款，即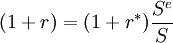
，则在任何一国存款均可。
其中， r表示以本币计价的资产收益率（年率），r * 表示外币计价的相似资产的平均收益率，S表示即期汇率（直接标价），Se表示预期将来某个时点（比如年末）的预期汇率。并且这里假设投资者是风险中性（Risk Neutral）。
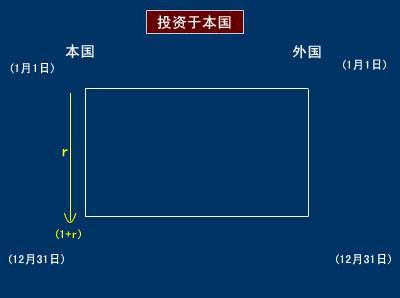
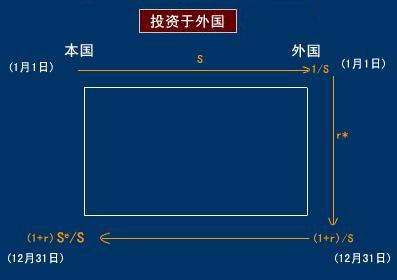
本国居民持有一单位本国货币，既可以将其存放于国内银行按国内利率取得收益，也可以将其按即期汇率S兑换成外国货币投放国外银行，按外国利率取得收益，用图—1、图—2来表示：
图—1
图—2
最终两者的收益趋于相等：
在风险中性的前提下，投资者只需比较一下两种资产的收益：如果收益不等，投资者就会涌向一种资产，资本涌入国会因投资的增加而收益率递减，而流出国的收益率则可能会抬高， 最终两者的收益趋于相等：
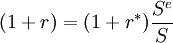(1)
如果预期汇率的变动率为ΔSe，则：
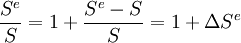(2)
那么式(1)可表述为：
(1 + r) = (1 + r * )(1 + ΔSe) = 1 + r * + ΔSe + r * ΔSe。
其中，r * ΔS是两个比率的积，是一个“二阶小量”，忽略不计，于是上式变为：
ΔSe = r − r * (3)
无抛补利率平价的含义：本国利率高于（低于）外国利率的差额等于本国货币的预期贬值（升值）幅度。
（二） 抛补的利率平价
定义：抛补利率平价，与无抛补利率平价相比，抛补的利率平价并未对投资者的风险偏好做出假定，即套利者在套利的时候，可以在期汇市场上签订与套利方向相反的远期外汇合同（掉期交易），确定在到期日交割时所使用的汇率水平。
通过签订远期外汇合同，按照合同中预先规定的期远期汇率进行交易，以达到套期保值的目的。由于套利者利用远期外汇市场固定了未来交易时的汇率，避免了汇率风险的影响，整个套利过程可以顺利实现。套利者如果在即期达成一笔一年期外汇交易，
用数学表达是：
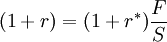(4)
其中，F (Forward rate)表示在即期（比如1月1日）公布的在1年后（比如12月31日）交割的远期汇率。它实际上是替代了公式(1）中的 Se （Expected Future Spot rate）。若令 f (Forward premium) 表示远期的升水（或贴水），即一国的远期汇率超过（低于）即期汇率的比率，则有
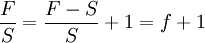(5）
那么，抛补的利率平价可更为清楚地表达为
f = r − r * (6）
在推算中，r * f同样被作为二阶小量被省去。
抛补利率平价含义：
（1）本国利率高于（低于）外国利率的差额等于本国货币的远期贴水（升水）。
（2）高利率国的货币在远期外汇市场上必定贴水，低利率国的货币在该市场上必定升水。如果国内利率高于国际利率水平，资金将流入国内牟取利润。
（3）抛补利率平价中，套利者不仅要考虑利率的收益，还要考虑由于汇率变动所产生的收益变动。
结论：在资本具有充分国际流动性的前提下，抛补与无抛补的利率平价均告诉我们：如果本国利率上升，超过利率平价所要求的水平，本币将会预期贬值；反之，则升值。
利率平价理论的思想起源可以追溯到l9世纪60年代。l9世纪90年代，研究远期外汇理论的德国经济学家沃尔塞·洛茨提出了利差与远期汇率的关系问题。
20世纪初期，凯恩斯第一个建立了古典利率平价模型，得出以下结论：
1、决定远期汇率的基本因素是货币短期存款利率之间的差额。
2、远期汇率围绕利率平价上下波动。
3、不论远期汇率与其利率平价偏离多大程度，获得足够利润的机会使套利者把资金转移到更有利的金融中心。
4、如果外汇交易被少数集团控制，或在主要交易人之间达成交易协议，那么，挂牌汇率可能偏离其利率平价。
5、套利资金有限，常常不能大到足以使远期汇率调整到其利率平价水平上。
6、在不兑换纸币的条件下，银行利率变化直接促使远期汇率重新调整。
20世纪30一40年代，保罗·艾因齐格运用动态均衡思想，发展了利率平价的动态理论。经过罗伯特·z·阿利布尔等人的进一步完善，现代利率平价理论框架趋于成熟。
现代利率平价理论的代表人物主要有特森·格鲁贝尔、沃费克尔和威利特等人。与传统的利率平价理论不同的是，利率平价的现代理论认为，套利者对远期外汇的超额需求不具有完全弹性（传统理论认为是呈完全弹性）。这就是说，远期汇率不仅受套利者行为的影响，而且也受到贸易商、投资者和中央银行等诸多外汇市场的参与者的影响。因此，远期汇率就不仅由套利决定，而且与套利者对即期汇率的预期有关。
对利率平价理论的评价[3]
自20世纪20年代利率平价被首次提出后，利率平价受到西方经济学家的重视。它与购买力平价所不同的是考察资本流动（而不是商品流动）与汇率决定之间的关系，它从一个侧面阐述了汇率变动的原因——资本在国际间的流动，利率平价同样并非是一个完善的汇率决定理论，对其的批评主要有：
1．利率平价的实现依据是国际金融市场上的“一价定律”， 但现实中，不仅完善的外汇市场没有普遍存在，而且许多国家实际对外汇实行管制并对资本流动进行限制。
“一价定律”的先决条件是：
（1）有效的且处于完全自由竞争状态的外汇市场。即需要一个有组织的即期和远期外汇市场，市场的信息能够非常有效地流通，从而消除可能出现的机会利润；
（2）无市场壁垒，资本在国际间的流动不受任何限制；
（3）交易成本很低或可以基本忽略不计。
2．在利率平价的关系式当中，并未能表明到底是利率平价决定汇率，还是即期汇率与远期汇率的差距来决定利率。
3．忽视利率结构问题。
利率平价说没有考虑交易成本。然而，交易成本却是很重要的因素。如果各种交易过高，就会影响套利收益，从而影响汇率与利率的关系。如果考虑交易成本，国际间的抛补套利活动在达到利率平价之前就会停止。
利率平价说假定不存在资本流动障碍，假定资金能顺利，不受限制地在国际间流动。但实际上，资金在国际间流动会受到外汇管制和外汇市场不发达等因素的阻碍。目前，只有在少数国际金融中心才存在完善的期汇市场，资金流动所受限制也少。
利率平价说还假定套利资金规模是无限的，故套利者能不断进行抛补套利，直到利率平价成立。
但事实上，从事抛补套利的资金并不是无限的。这是因为：
与持有国内资产相比较，持有国外资产具有额外的风险。随着套利资金的递增，其风险也是递增的。
套利还存在机会成本，由于套利的资金数额越大，则为预防和安全之需而持有的现金就越少。而且这一机会成本也是随套利资金的增加而递增的。基于以上因素，在现实世界中，利率平价往往难以成立。
- ↑ 夏大慰,刘勤主编;刘凤委,张英奎,刘勤等编著.公司战略与风险管理.中国财政经济出版社,2009.04.
- ↑ 朱孟楠.厦门大学.国际金融学. 第二章 外汇与汇率 第四节 汇率理论及其评价
- ↑ 3.0 3.1 《国际经济学》.第十章 汇率的决定.第三节 利率平价理论.西北师范大学 经济管理学院
本条目由以下用户参与贡献
Angle Roh,苦行者,山林,funwmy,Zfj3000,18°@鷺島,Dan,Cabbage,ROURTW,泡芙小姐,HEHE林,Tiffany,罗茜,Lin,张介平,Tracy,M id 33102b7c5aa30123ac49f7d914825224,M id 0fda389224938afbbdc3e0bd9945ebee.评论(共18条)
r − r * = ΔEe 应该 是r − r * = ΔEe（1+r)吧，别误人了
感谢提出错误之处，现已对内容进行了整理，不足之处，欢迎指正
r − r * = ΔEe 应该 是r − r * = ΔEe（1+r)吧，别误人了
由于ΔEe（1+r)=ΔEe+ΔEe*r，而ΔEe*r相对于其他几个值是很小的，为简便，可以将其省略。类似的省略并不少见
感谢Derek8687的提醒，已将缺失部分进行补充。
MBA智库百科是可以自由参与编辑的百科，发现错误和不足您也可以参与修改和编辑哦！
r − r * = ΔEe 应该 是r − r * = ΔEe（1+r)吧，别误人了
你指出错误的地方是好事，但你用“误人”两个字就不对了。人家辛苦写出来的东西，你要尊重别人的劳动。
你指出错误的地方是好事，但你用“误人”两个字就不对了。人家辛苦写出来的东西，你要尊重别人的劳动。
你说的那一项因为太小被忽略了。
Ee △= —— - 1 吧？ E