保险精算
出自 MBA智库百科(https://wiki.mbalib.com/)
目录 |
保险精算是指运用数学、统计学、金融学、保险学及人口学等学科的知识与原理，去解决商业保险与各种社会保障业务中需要精确计算的项目，如死亡率的测定、生命表的构造、费率的厘定、准备金的计提以及业务盈余分配等，以此保证保险经营的稳定性和安全性。保险精算通常可分为寿险精算和意外精算两类。[1]
保险精算的职能[2]
对于经营保险业务的各类保险公司，在其经营管理的各个环节上，如计划、统计、展业、财务、投资、研究及培训等方面，都需要精算发挥其特有的作用。保险精算具有计算、分析、预测、服务等多项职能。这些职能可以通过保险精算师的职能具体表现出来。
(1)根据精算理论，科学地厘定各类险种的保险费率。
(4)分析保险公司的年度利润来源。
(5)根据保险市场的变化、对保险的需求及地区特点为保险公司设计新险种。
(6)参与保险公司的计划、展业、投资、财务等的经营管理决策；参与编制保险公司的各项年度报表(如财务报表、经营报表、税务报表、呈送给保险监督部门的报表等)，负责其中精算部分的计算。
(7)协助职能部门根据统计资料研究各险科的效益，以及保险费率的调整，以适应市场竞争的需要，以及编制内部报告。
(8)研究灾害损失的趋势，预测本公司的偿付能力；为防灾技术提供资料和研究手段；参与防灾、防损及风险管理。
(9)研究再保险的设置、再保险费率及再保险对本公司经营的作用。
保险精算的基本原理[3]
一、大数定律
(一)切比雪夫大数定律
设X1，X2，…，Xn是由相互独立的随机变量所构成的序列，每一随机变量都有有限的方差，并且它们有公共上界，即：
Var(X1)≤C，Var(X2)≤C，…，Var(Xn)≤C
则对于任意的Ξ>O，都有：
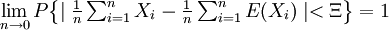
切比雪夫大数定律阐述的是大量随机因素的平均效果与其数学期望有较大偏差的可能性越来越小的规律。从风险的角度看，它表明，如果以Xi表示第i个风险单位的未来损失，则当n很大时，n个风险单位未来损失和以概率1接近它们的期望值。这就是保险人把未来损失的期望值作为纯保险费的主要根据。
当保险人承保了n个相互独立的保险标的后，尽管每个风险单位的实际损失Xi不会等于其期望值E(Xi)，但当保险标的数n足够大时，保险标的的平均损失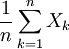
与其损失的平均期望值
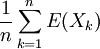几乎相等。换言之，如果保险人按照每个风险单位的未来损失期望值作为纯保险费来收取，则当其聚集风险单位足够多时，这些纯保险费将足够支付保险人未来作出的损失赔偿。
(二)贝努利大数定律
在事件A发生的概率为P的n次贝努利模型中，令μn以表示A发生的次数，则对Ξ>0，有：
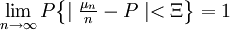
需要注意的是，该定律的结论虽然简单，但其意义却相当深刻。将与事件A有关的试验重复n次，结果一共出现μn次，则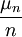
便是事件A在n次试验中出现的频率。贝努利大数定律表明，当n很大时，频率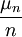以概率1接近概率P，正好验证了“任何事件的概率是它的频率的稳定值”这一结论。这一定律提供了以频率解释概率的数理基础，对于保险人利用统计资料来估测未来损失概率具有重要意义。
保险标的的损失概率决定了保险产品的价格。保险人利用以往的经验数据求得保险标的发生的频率，并以此频率值作为损失概率的估计值。尽管损失频率与损失概率之间不可避免地存在偏差，但根据贝努利大数定律，损失概率的估计值与实际损失概率之间的偏差，随着保险标的数目的增加而减小。
二、保险定价原理
保险产品的定价是指保险产品价格(即保险费)的确定过程。保险费是保险人为承担确定保险责任而向投保人收取的费用。保险费的确定涉及与险种相关的保险标的类别、危险程度、保险责任范围、保险期限等因素。保险人应在全面、科学地考虑这些因素的基础上来定价。
保险产品的定价必须遵循充足性、合理性、公平性原则。充足性是指保险产品的费率应该保证保险人足够抵补一切可能发生的给付和相关费用。费率不足，将会导致保险公司缺乏偿付能力。合理性是指保险费不应超出保险人的合理支出(费用、利润等)的范围。公平性是指保险人承担的保险责任与投保人交付的保险费对等。需要注意的是，合理性是针对险种的平均费率而言的，而合理的费率不一定是公平的费率。公平性并不是要求保险人实现绝对的公平，而是要求保险人应当根据保险标的的风险状况进行风险分类，对不同的类别确定不同的价格，以实现相对公平。
保险费由两部分构成：①纯保险费，即按照保险人未来保险金支出计算所得的部分；②附加保险费，即保险人用于经营业务所需的费用和利润的部分。在本章的后面几节中，我们只研究与纯保险费相关的计算原理。
纯保险费的计算必须在精算等价原理下进行。精算等价原理又称收付平衡原理。
趸缴纯保险费=E(保险人未来收取的分期纯保险费的现值)=E(保险人未来支付的保险金的现值)
对于非寿险来说，纯保费的计算公式为：纯保险费=E(保险人未来支付的保险金)
这里，寿险与非寿险的计算公式的主要差别在于：①由于寿险合同具有长期性，所以必须考虑利息的作用；而非寿险合同的保险期限通常为1年或更短，可以忽略利息的影响。②寿险保险费的交付方式可以是趸缴或分期缴纳，而非寿险通常是一次性缴纳。
根据精算等价原理我们可以确定各种险种的纯保险费。
保险精算的产生和发展[2]
保险精算是从人寿保险经营的窘境中应运而生的。人寿保险的前身是欧洲中世纪的基尔特(Guild)制度。18世纪中期以前，英国早期资格最老的组织首先要数于1706年在伦敦成立的协和保险社。1721年，经特许成立的皇家交易保险公司和伦敦保险公司开始经营人寿保险业务，此外，还有一些捐助团体及联盟协会也经营人寿保险业务。当时，寿险的保费采用赋课制，未将年龄大小、死亡率高低等与保费挂钩，有关计算单一、粗糙，考虑的因素少，因而使寿险经营缺乏严密的科学基础。
在过去极端缺乏统计资料的情况下，承保人对各种风险进行了估计并承保了这些风险。在17世纪后半叶，世界上有两位保险精算创始人研究人寿保险计算原理取得突破性进展，一位是荷兰的政治家维德(Jean de Witt)，另一位是英国天文学家赫利(Edmund Halley)。
前者倡导了一种终身年金现值的计算方法，为国家的年金公债发行提供了科学依据；后者在研究人类死亡率的基础上，发明了生命表，从而使年金价值的计算更为精确。18世纪四五十年代，辛浦森(Thomas Simpson)根据赫利的生命表，制作出依照死亡率的提高而递增的费率表，陶德森(Jams Dodson)依据年龄之差等因素找出了计算保险费的方法。
如上所述，保险精算首先产生于寿险经营，这是因为寿险精算与寿险经营密不可分，而且还是寿险经营的内在要求。所以，寿险精算反过来极大地推动了寿险业的发展，并最终形成了一整套的寿险精算体系。与寿险精算相比，非寿险精算相对落后。长期以来，人们在习惯上把涉及寿险精算的科学称为精算学，并一直沿用至今。因此，现在所说的精算学，既包括整个保险学范围的保险精算学，又可理解为寿险专有的精算学。但是，随着科学技术的进步，在第二次世界大战后，非寿险精算技术和理论日益完善。到20世纪70年代，非寿险精算技术已发展成为一门独立的分支学科，人们称之为非寿险精算学。虽然非寿险精算学与传统的精算学有着许多联系，然而其内容和理论基础是有根本区别的，是两个不同的学科。因此，非寿险精算学既属于保险精算学的范畴，又不同于传统的精算学。
由于非寿险精算学在保险业的发展中发挥着日益重要的作用，因而备受各国保险界的重视，现已成为保险公司在激烈的竞争环境中得以生存和发展的重要因素之一。目前，国外已有非寿险精算师的职业和相应的学会。例如，美国有灾害精算学会，并有意外精算学会负责颁发财产和责任保险精算师证书；日本有损害保险学会；等等。
