STAR模型
出自 MBA智库百科(https://wiki.mbalib.com/)
目錄 |
STAR模型全稱為平滑轉移自回歸模型(smooth transition autoregression)，是非線性時間序列模型中的參數模型，各個參數有很強的經濟背景，始於2003年諾貝爾經濟學獎得主Granger和瑞典著名統計學家
於1993 年的研究論文, 此後大量的理論和應用研究發現這一模型確實很好的模擬了商業周期、匯率以及失業率等經濟、金融時間序列對均衡的偏離和回覆現象。
STAR模型的內涵[1]
STAR模型的經濟學含義是經濟集合體中所有變化主要由不同行為個體變化引起，並非所有個體同時對某個經濟信號做出反映而相互影響。因此不同於離散轉移模型，平滑轉移回歸模型的轉移是基於轉移變數的連續過程(Hansen，1999)。當不確定區制轉變的時間且新區制還未產生的時候，平滑轉移回歸模型有效的體現了區制轉移行為，所以該模型能夠捕捉在轉移階段變數的動態特征。同時具備非線性和區制轉移的特征使得該模型成為研究經濟變數的重要工具。
選擇STAR模型對中國實際匯率非線性態勢進行實證預測研究的原因是：平滑轉移自回歸模型不用像馬爾可夫機制轉換模型那樣需要提出預先假設、捕捉不到狀態的變化；同時門限模型的錯誤設定問題也在一定程度上得到緩解；而ARCH類模型只能解決殘差的非線性問題；只有STAR模型可以追蹤在兩個極端機制之間的平滑改變或漸進變化，最易模擬匯率動態變化的非線性路徑。
STAR模型的形式及線性檢驗[2]
設STAR模型形式為
公式一：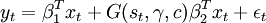
其中β1,β2表示參數向量，
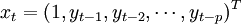
εt˜i.i.d.N(0,σ2)
G(st,γ,c)為轉移函數，st為轉移變數。常用的轉移函數形式包括Logistis形式(LSTAR)和指數形式(ESTAR)。
Logistis形式的轉移函數為
公式二：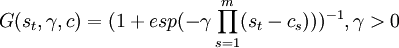
參數γ決定了機制轉換的平滑程度，γ越大機制轉換越陡峭。當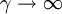
時，模型的指數部分衰減得非常快，模型的轉換幾乎是瞬間完成的。
指數形式的轉移函數為
公式三：G(st,γ,c) = 1 − esp( − γ(st − c)2),γ > 0
顯然，ESTAR的轉移函數關於st = c對稱；若轉換速度參數
或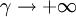
，G(st,γ,c)都將退化為常數(O或1)。
STAR模型線性檢驗的基本思想是令H0:γ = 0，進而G(·)=1／2，此時模型將退化為線性模型。但這樣會使參數向量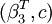
成為無法識別的冗餘參數。針對這一問題，Luukkonen等提出將轉移函數按照泰勒級數展開，併在此基礎上構造LM類型的統計量(以下簡稱LST統計量)．對於LSTAR模型，將轉移函數按照3階泰勒級數展開得到：
公式四：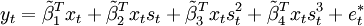
其中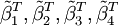
表示估計後的參數向量。
原假設轉化為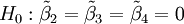
，使用的LM統計量為
公式五：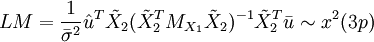
其中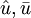
表示殘差誤差的估計向量
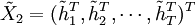
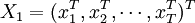
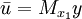
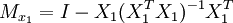
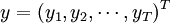
在實際應用時，STAR模型線性檢驗的步驟為
1)線上性原假設下估計模型，計算其殘差平方和SSR0；2)估計輔助回歸式，即公式四，計算其殘差平方和SSR1；3)根據公式六或公式七計算統計量的值；
公式六：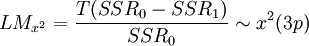
公式七：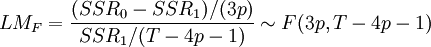
Gonzalez等指出在一般情況下，該統計量具有較好的檢驗水平和功效，但如果樣本容量較小，則會出現嚴重的檢驗水平扭曲，並且如果樣本容量小於4p，該檢驗失效。
STAR模型的結構構成[3]
STAR模型的結構是圍繞以下三個關係組織的：
(1)資本積累影響利潤的關係：在一定的實際資本積累與增長水平下，以當前價格表示的需求可按收入項目予以計算(同其他模型相反，這裡沒有關於工資率的方程，而且工資單一利潤分紅是直接決定的)。
(2)利潤影響資本積累的關係：廠商按現行價格的投資依自籌資金(如在FIFI和DECA模型中那樣)以及外部投資可能性兩者而定(這些又轉而依靠家庭儲蓄而定)。
(3)增長影響利潤的關係：利潤水平依實際產出和資本存量，以及以往年份繼承下來的金融結構而定。
前兩組關係完全決定了現行價格(按價值量)和特別是名義生產水平以及有效利潤三者之間的平衡，但是它們必須與增長率相一致。因此，價格水平的決定必須使生產在價值量與實物量間達到一致。這裡沒有明確的價格方程(如在ZOGOL或DECA模型中那樣)，只有一種“隱含的”使要求的與實現的利潤率相均衡的確定方法(Mazier，1975)。
STAT模型的結構看上去十分原始；如果根據凱恩斯主義的價值觀來看，它引入了實際生產中影響供給的因素(如FIFI模型所做的)。實物一價值分配決定是模型的核心部分，並能夠理解現實流行的停滯膨脹。不過，它來自對歷史的模擬，即通貨膨脹的決定是有傾向性的(Boyer等，1973)，而且對確定價格水平用的利潤增長關係的有效性表示懷疑。廠商獲得的利益在模型的動態特性中也起著重要作用[它同R．M·古德溫(Goodwin)理論模型具有某些相似之處](R．M．Goodwin，1951)。
