Mankiw-Romer-Weil模型

出自 MBA智库百科(https://wiki.mbalib.com/)

Mankiw-Romer-Weil模型（Mankiw-Romer-Weil model，簡稱MRW模型）

　　格裡高利·曼昆、大衛·羅默及大衛·威爾(Gregory Mankiw，David Romer，David Weil)為增長回歸提供了一個簡單的框架，從此以後稱為MRW模型。MRW模型在繼承傳統增長理論的基礎上，為實證研究提供了一個較好的起點。

　　該模型將1960—1985年期間的國家分為3個樣本：98個非石油生產國，76個發展中國家（不包括小國家和統計數據有疑問的國家），22個人口超過100萬的OECD國家，並利用規模報酬不變的柯布-道格拉斯生產函數為工具：

　　Y = K^αH^β(AL)^{1 − α − β}　　　　(1)

　　K表示物質資本，H表示人力資本，L代表以A為技術效率指數的勞動供給。MRW認為物質資本和人力資本投資率各自固定值為S_k和S_h，折舊率為δ，各國內生技術進步增長率為g，勞動力以不同速度n增長，這類似於包含增量人力資本的索羅模型，以及國家擁有同樣增長率的假定，各國起始的效率水平A(0)看做是隨機量，作為誤差項，通過估計近似的穩定狀態，MRW模型可推出下麵的方程。

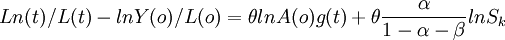
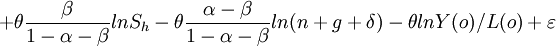　　　　　　(2)

　　θ = 1 − e _{− k}，λ表示一個國家趨向穩定狀態的趨同率，測量國家以多快速度達到它們長期均衡路徑的方法，可表示以下形式。

　　dlny(t) / dt = λ[lny ^* − lny(t)]

　　趨向速度為　　λ = (n + g + δ)(1 − α − β)　　　　(3)

　　眾所周知，丹尼森所做的工作無法解決“索羅餘值”問題。MRW模型通過引入人力資本，用物質資本投資、人力資本投資、人口增長率3個變數建立了一個擴展的計量模型，證明瞭新古典增長率模型的有效性，認為人力資本緩了物質資本的邊際收益遞減速度，儘管趨同速度比傳統的索羅模型所喻示的要慢，但不能以經濟增長率與起始人均收入是否呈負相關而簡單地證偽新古典增長理論與新增長理論。