算術平均數
出自 MBA智库百科(https://wiki.mbalib.com/)
算術平均數(Arithmetic Average)
目錄 |
算術平均數(算術平均法)是總體各單位某一數量標誌的平均數。通過算術平均數,可以用來求出一定觀察期內預測目標的時間數列的算術平均數作為下期預測值的一種最簡單的時序預測法。
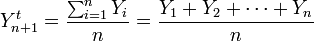
式中,
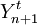 =第n+1期銷售量的預測值
=第n+1期銷售量的預測值
Yi=第i期的實際銷售量
n=所選期數
基本計算公式為:
1、簡單算術平均法
2、加權算術平均法
該方法的優點是計算簡單,而缺點是計算平均數時沒有考慮到近期的變動趨勢,因而預測值與實際值往往會發生較大的誤差。
通常適用於預測銷售比較穩定的產品。如沒有季節性變化的糧油食品和日常用品等。
算術平均法根據企業過去按時間順序排列的銷售量(或銷售額)的歷史數據,計算其平均數,並將該平均數作為計劃期的銷售預測數。
其計算公式為:
計劃期銷售量(額)預測數=各期銷售量(額)之和÷期數。
算術平均數與強度相對數的比較
1、概念不同。強度相對數是兩個有聯繫而性質不同的總體指標值對比而形成相對數指標。算術平均數是反映同質總體各單位某一數量標誌值一般水平的指標。
2、主要作用不同。強度相對數反映現象的密度、強度和普遍程度。算術平均數反映同一現象總體的一般水平。
3、分子分母的依存關係不同。算術平均數的分子與分母間存在直接的依存關係。強度相對指標的分子、分母之間無依存關係。
1、簡單算術平均法
計算公式:
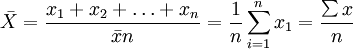
其中:---  算術平均數,X---各單位標誌值(變數值),n---總體單位數(項數)。
算術平均數,X---各單位標誌值(變數值),n---總體單位數(項數)。
運用條件:統計資料未分組時
例:某公司下屬各店職工按工齡分組情況
工齡 組中值
x人 數 f 一店 二店 三店 四店 五店 0~2年
2 ~5年
5 ~10年
10 ~20年1.0
3.5
7.5
15.01
1
1
17
7
7
725
25
25
251
3
6
1010
6
3
1合計 — 4 28 100 20 20 平均工齡 — 6.75 6.75 6.75 10.325 3.425
2、加權算術平均法
計算公式:
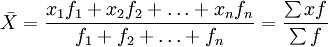
其中: ----代表算術平均數,x 代表各單位標誌值(變數值),f 代表各組單位數(項數)。
----代表算術平均數,x 代表各單位標誌值(變數值),f 代表各組單位數(項數)。
運用條件:統計資料分組時從前面的表中資料可以看出一、二、三店人數相差很遠,但平均工齡相等。四、五店人數相等,但平均工齡相差很大。由此我們不難得出如下結論:平均數水平高低受兩個因素的影響:
(1)受各組變數值( x )大小的影響
(2)受各組權數(f)大小的影響。(絕對權數表現為次數、頻數,相對權數表現為頻率)。
1、平均數與總體單位數的積等於總體標誌總量
2、若每個變數值 (X ) 加減一任意常數α,則平均數也加減這個任意值α。
3、若每個變數值 (X)乘以一任意常數α,則平均數也乘以這個任意值α。
4、若每個變數值( X)除以一任意常數α,則平均數也除以這個任意值α。
5、各個變數值(X)與算術平均數 的離差和為零。
的離差和為零。
6、各個變數值(X)與算術平均數 的離差平方和為最小值。
的離差平方和為最小值。







