集聚因數

出自 MBA智库百科(https://wiki.mbalib.com/)

　　集聚因數是指一定量的生產集中在特定場所帶來的生產或銷售成本降低。與此相反，分散因數則是集聚的反作用力，是隨著消除這種集中而帶來的生產成本降低。

　　集聚因數的作用分為兩種形態：一是由經營規模的擴大而產生的生產集聚。大規模經營相對於明顯分散的小規模經營可以說是一種集聚，這種集聚一般是由“大規模經營的利益”或“大規模生產的利益”所產生。二是由多種企業在空間上集中產生的集聚。這種集聚利益是通過企業間的協作、分工和基礎設施的共同利用所帶來的。

　　集聚又可分為純粹集聚和偶然集聚兩種類型：純粹集聚是集聚因數的必然歸屬的結果，即由技術性和經濟性的集聚利益產生的集聚，也稱為技術性集聚；偶然集聚是純粹集聚之外的集聚，如運費指向和勞動費指向的結果帶來的工業集中。

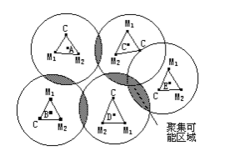
　　韋伯進一步研究了集聚利益對運費指向或勞動費指向區位的影響。他認為，集聚節約額比運費（或勞動費）指向帶來的生產費用節約額大時，便產生集聚。一般而言，發生集聚指向可能性大的區域是多數工廠互相臨近的區域。如圖所示，五個工廠不考慮集聚情況下的費用最小地點在圖中的各處，假定當三個工廠集聚可由集聚利益使單位產品節約成本2個貨幣單位。為得到這一集聚利益，工廠必須放棄原有費用最小地點，從而增加運費。工廠的移動的前提必須是增加的運費低於2個貨幣單位。圖中圍繞各工廠的封閉連線，是同由集聚利益而節約的成本相等的運費增加額曲線，也即臨界等費用線。在斜線部分三個工廠集聚可以帶來2個單位成本的節約，並且又都在臨界等費用線內側，是最有可能發生集聚的區域。

　　為了判斷集聚的可能性，他提出了加工繫數的概念：即加工繫數等於單位區位重量的加工價值。該繫數高的工業，集聚的可能性也大；相反，集聚的可能性就小。