財務困境預測模型
出自 MBA智库百科(https://wiki.mbalib.com/)
目錄 |
財務困境預測模型研究的基本問題——財務困境
財務困境(Financial distress)又稱“財務危機”(Financial crisis),最嚴重的財務困境是“企業破產” (Bankruptcy)。企業因財務困境導致破產實際上是一種違約行為,所以財務困境又可稱為“違約風險”(Default risk)。
事實上,企業陷入財務困境是一個逐步的過程,通常從財務正常漸漸發展到財務危機。實踐中,大多數企業的財務困境都是由財務狀況正常到逐步惡化,最終導致財務困境或破產的。因此,企業的財務困境不但具有先兆,而且是可預測的。正確地預測企業財務困境,對於保護投資者和債權人的利益、對於經營者防範財務危機、對於政府管理部門監控上市公司質量和證券市場風險,都具有重要的現實意義。縱觀財務困境判定和預測模型的研究,涉及到三個基本問題:
- 1、財務困境的定義;
- 2、預測變數或判定指標的選擇;
- 3、計量方法的選擇。
- 預測變數或判定指標的選擇
財務困境預測模型因所用的信息類型不同分為財務指標信息類模型、現金流量信息類模型和市場收益率信息類模型。
1、財務指標信息類模型
Ahman(1968)等學者(Ahman,Haldeman和Narayanan,1980;Platt和Platt, 1991)使用常規的財務指標,如負債比率、流動比率、凈資產收益率和資產周轉速度等,作為預測模型的變數進行財務困境預測。
儘管財務指標廣泛且有效地應用於財務困境預測模型,但如何選擇財務指標及是否存在最佳的財務指標來預測財務困境發生的概率卻一直存在分歧。Harmer (1983)指出被選財務指標的相對獨立性能提高模型的預測能力。Boritz(1991)區分出65個之多的財務指標作為預測變數。但是,自Z模型 (1968)和ZETA模型(1977)發明後,還未出現更好的使用財務指標於預測財務困境的模型。
2、現金流量信息類模型
現金流量類信息的財務困境預測模型基於一個理財學的基本原理:公司的價值應等於預期的現金流量的凈現值。如果公司沒有足夠的現金支付到期債務,而且又無其他途徑獲得資金時,那麼公司最終將破產。因此,過去和現在的現金流量應能很好地反映公司的價值和破產概率。
在Gentry,Newbold和Whitford(1985a;1985b)研究的基礎上,Aziz、Emanuel和Lawson(1988)發展了現金流量信息預測財務困境模型。公司的價值來自經營的、政府的、債權人的、股東的現金流量的折現值之和。他們根據配對的破產公司和非破產公司的數據,發現在破產前5年內兩類公司的經營現金流量均值和現金支付的所得稅均值有顯著的差異。顯然,這一結果是符合現實的。破產公司與非破產公司的經營性現金流量會因投資質量和經營效率的差異而不同,二者以現金支付的所得稅也會因稅收會計的處理差異而不同。Aziz、Emanuel和Lawson(1989)比較了Z 模型、ZETA模型、現金流量模型預測企業發生財務困境的準確率,發現現金流量模型的預測效果較好。
3、市場收益率信息類模型
Beaver(1968)是使用股票市場收益率信息進行財務困境預測研究的先驅。他發現在有效的資本市場里,股票收益率也如同財務指標一樣可以預測破產,但時間略滯後。Altman和Brenner(1981)的研究表明,破產公司的股票在破產前至少1年內在資本市場上表現欠佳。Clark和Weinstein(1983)發現破產公司股票在破產前至少3年記憶體在負的市場收益率。然而,他們也發現破產公告仍然向市場釋放了新的信息。破產公司股票在破產公告日前後的兩個月時間區段內平均將經歷26%的資本損失。
Aharony,Jones和Swary(1980)提出了一個基於市場收益率方差的破產預測模型。他們發現在正式的破產公告日之前的4年內,破產公司的股票的市場收益率方差與一般公司存在差異。在接近破產公告日時,破產公司的股票的市場收益率方差變大。
- 計量方法的選擇
財務困境的預測模型因選用變數多少不同分為
1、單變數預測模型
2、多變數預測模型:多變數預測模型因使用計量方法不同分為
- 1)線性判定模型
- 2)線性概率模型
- 3)Logistic回歸模型。
此外,值得註意的是,近年來財務困境預測的研究方法又有新的進展,網路神經遺傳方法已經開始被應用於構建和估計財務困境預測模型。
上市公司財務困境預測模型比較研究[1]
一、建模方法
1.統計方法
採用MDA、Logistic回歸、近鄰法,以及分類和回歸樹(CART)四種方法建立統計模型,其中前兩者屬於參數法,後兩者屬於非參數方法。
MDA和Logistic回歸都屬於多元統計學方法,基本思路是由一些已知類別的訓練樣本,根據判別準則建立判別函數(模型),用來對新樣本進行分類。這兩種方法的最大優點在於具有明顯的解釋性,存在的缺陷是過於嚴格的前提條件。如兩者都對變數之間多重共線性敏感,且MDA要求數據服從多元正態分佈和等協方差。
近鄰法根據新樣本在特征空間中K個近鄰樣本中的多數樣本的類別來進行分類,因此具有直觀、無需先驗統計知識、無需學習等特點。但當樣本的維數較高時,存在所謂的“維數禍根”——對高維數據,即使樣本量很大,其散佈在高維空間中仍顯得非常稀疏,這使得“近鄰”的方法不可靠
CART是一種現代非參數統計方法,它根據一定的標準,運用二分法,通過建立二元分類樹來對新樣本進行預測。CART模型宜於理解,能處理缺失數據,並且對雜訊有一定的魯棒性。它的缺點是,作為一種前向選擇方法,當它引入新的分類規則時並沒有考慮前面的分類方法,因而有可能同一個分類變數會重覆出現但判別點發生變化。
2.神經網路方法
神經網路是由大量的簡單處理單元相互聯結組成的複雜網路系統。作為非參數的分類方法,它剋服了選擇模型函數形式的困難,同時對樣本及變數的分佈特征沒有限制。採用在財務困境預測研究中應用最廣的三種神經網路:反向傳播網路(BPNN)、概率神經網路(PNN)和學習矢量量化網路(LVQ)來建立模型。
BPNN是應用最廣泛的一種神經網路。在建立財務困境預測模型時,一般選三層BPNN:輸入層由代表財務比率的節點構成;隱層節點個數由經驗試錯法確定;輸出層僅有一個節點,該節點輸出值大於預設閾值時為一類,小於預設閾值時為另一類。
PNN主要是用估計各個類別核密度的方法完成樣本分類。當用於財務困境預測時,PNN通常取三層:輸入層節點數等於建模所用財務比率個數;中間層節點數等於訓練集樣本個數;輸出層節點數等於樣本類別數。與BPNN相比,PNN的優勢在於要估計的參數少,訓練時間短,而且能夠對模型生成的結果做出概率上的解釋。
LVQ是在自組織映射神經網路基礎上改進的一種有導師監督分類器,它允許對輸入樣本按照所屬的類別進行指定。用於財務困境預測的LVQ由三層節點組成。輸入層節點數等於建模所用的財務比率個數,輸出層節點數對應於輸入樣本的類別個數。與前兩種神經網路不同的是,LVQ競爭層的每個節點只與輸出層的一個節點相連接,即被指定屬於這個輸出層節點所對應的類別。也就是說,競爭層將輸入矢量分成不同子類,輸出層負責將競爭隱層的子類轉換為使用者定義的類別。
神經網路具有一些統計方法無法比擬的優點,如:對數據分佈的要求不嚴格;非線性的函數映射方式;高魯棒性和自適應性等。然而,由於神經網路缺乏統一的數學理論,在如何確定網路結構、如何提高模型的解釋性、過學習和局部極小點等問題上還未有實質突破,並且實際效果也不太穩定。
3.交叉驗證
所謂m重交叉驗證,就是將樣本總數為n的樣本集隨機地分成m個不相交的組,每組有nlm個樣本。用(m-1)個組的樣本訓練分類器,並用剩餘的1個組的樣本作為測試集測試分類器,求得一測試誤差。重覆這一過程,直到m個組中的每一組都成為過一次測試集為止。將m個組所對應濺試誤差的平均值作為分類器在整個樣本集上的測試誤差。交叉驗證能減少估計偏差,從而更客觀地評價模型。
二、樣本和變數選擇
1.樣本選擇
我國滬深股市1998~2002五年間258家公司選作建模樣本,其。申ST公司和配對的非ST公司各129家,將2003,2004兩年內被ST的106家公司和246家非ST公司作為獨立的預測集,所有610家公司假設是在t年被ST或未被ST。樣本選擇標準如下:
1)從1998~2002五年間所有的151家sT公司中剔除因“其它狀況異常”而被ST的公司22家,保留因“財務狀況異常”(“連續兩年虧損”或“每股凈資產低於股票面值”)而被ST的129家公司作為財務困境公司;根據同行業與總資產規模相當標準,從同一財務年度選出129家配對的非ST公司;
2)在構造預測集時,為了評價模型實際預測效果,將2003-2004兩年內所有ST公司全部選人預測集,沒有進行任何剔除;在選擇非ST樣本時,同樣為了評價模型實際預測效果,沒有根據配對原則來選,只是隨機地選取了這兩年內246家非ST公司;
2.比率選擇
由於缺乏具體的經濟理論指導,而公司被ST的本質原因又不盡相同,所以很難用簡單的幾個財務比率對財務困境進行充分描述。研究者選用的財務比率有所差異,通常選擇儘可能多的財務比率,這些不同的財務比率反映著企業不同的財務側面,如盈利能力、償債能力、營運能力和現金能力等方面。從研究結果來看,得出的預測財務困境最有效的財務比率也不盡相同心。財務比率共有41個(見下表),反映了企業財務狀況的各個方面,以便從中找出統計檢驗顯著性強的比率進行建模
三、模型選擇
為了消除財務比率量綱和數量級差異的影響,首先對原始數據進行標準化,即變換為均值為0和標準差為1的新數據。然後進行ST公司和非ST公司財務比率差異的單變數檢驗。根據檢驗結果,首先選出兩類公司間具有顯著差異(P<0.05)的比率:被ST前的(t-2)財政年度包括X3 − X9,X11,X15,X17 − X26,X19,X31,X37,X40,X41;被ST前的(t-3)財政年度包括X5 − X8,X14,X15,X17,X18,X20,X22 − X26,X28,X29,X37 − X41
1.統計模型
MDA和Logistic回歸模型預測變數集
| (t-2) | (t-3) |
|---|---|
| X6,X17,X23,X24,X25 | X7,X20,X28,X38,X41 |
對於MDA和longistic回歸,首先採用10重交叉驗證+和逐步回歸選擇變數方法對上述初選的比率集進行再次篩選,如果某一財務比率在10次結果中出現了4次以上。則被選人。然後經過多重共線性檢驗剔除冗餘變數,最終選出的預測變數如表2
對於近鄰法,仍採用上述財務比率集{X_6,X_17,X_23,X_24,X_25}和{X_7,X_20,X_28,X_38,X_41}作為(t-2)和(t-3)年模型的預測變數集。並應用10重交叉驗證選擇近鄰數K,具體如表3。可見,最近鄰(K=1)具有最佳分類效果
近鄰法K選擇的10重交叉驗證分析
| K | (t-2) | (t-3) | ||||
|---|---|---|---|---|---|---|
| 總正確數 | 一類錯誤數 | 二類錯誤數 | 總正確數 | 一類錯誤數 | 二類錯誤數 | |
| 1 | 24.4 | 0.7 | 0.7 | 23.5 | 1.1 | 1.2 |
| 3 | 23 | 2 | 0.8 | 20.7 | 2.6 | 2.5 |
| 5 | 22.2 | 2.3 | 1.3 | 19.8 | 3.1 | 2.9 |
| 7 | 22.3 | 2.4 | 1.1 | 19.7 | 3.1 | 3 |
| 9 | 22.5 | 2.4 | 0.9 | 19.9 | 3.2 | 2.7 |
註:表3-表7中數據均為10次交叉測試結果的平均值
由於決策樹屬於非參數化的自上而下的歸納學習演算法,所以對於CART模型,不必對變數進行篩選
但是,為防止“過擬合”發生,需要對樹進行修剪,修剪程度的大小由10重交叉驗證確定,結果如下表。可見,未剪枝的CART在10個測試集上的平均效果最好,但與剪枝2的效果沒有明顯差別,根據Occam剃刀原理㈨,選用剪枝度為2的CART模型
CART剪枝度選擇的10重交叉驗證分析
| 剪枝程度 | (t-2) | (t-3) | ||||
|---|---|---|---|---|---|---|
| 總正確數 | 一類錯誤數 | 二類錯誤數 | 總正確數 | 一類錯誤數 | 二類錯誤數 | |
| 0 | 24.1 | 1.1 | 0.6 | 22.3 | 1.9 | 1.8 |
| 1 | 23.8 | 1.2 | 0.8 | 21.9 | 1.9 | 2 |
| 2 | 23.6 | 1.1 | 1.1 | 21.6 | 1.9 | 2.3 |
| 3 | 23 | 1.3 | 1.5 | 21.3 | 1.8 | 2.7 |
2.神經網路模型
由於神經網路自學習能力和非線性映射能力很強,輸入變數間是否存在多重共線性對數據處理結果的影響不大,因此在構建神經網路模型時沒有進行變數篩選,而僅僅使所選財務比率儘可能包含比較多的信息。選取了X3、X7、X13、X15、X18、X_20、X_24、X25、X29和X41共10個比率作為神經網路的輸入變數,它們全面地反映了企業的盈利能力、償債能力、營運能力和現金能力等各個方面。
對於BPNN,採用小隨機數作為初始權值,以使初始點儘量避免局部極小。隱層節點數由經驗公式確定。
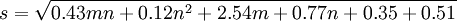 (1)
(1)
其中,s值經四舍五人取整後作為中間層節點數,m為輸入層節點數,n為輸出層節點數。由上可知m=10,n=1計算得中間層的節點數為6。採用10重交叉驗證確定BPNN的訓練誤差參數,結果如表5。可見,對於(t-2)年數據,誤差參數為0。06時BPNN的平均效果最好;對於(t-3)年數據,誤差參數為0.09時BPNN的平均效果最好
BPNN誤差參數的10重交叉驗證分析
| 誤差 | (t-2) | (t-3) | ||||
|---|---|---|---|---|---|---|
| 總正確數 | 一類錯誤數 | 二類錯誤數 | 總正確數 | 一類錯誤數 | 二類錯誤數 | |
| 0.05 | 23.1 | 1.6 | 1.1 | 20.8 | 2.1 | 2.9 |
| 0.06 | 23.6 | 1 | 1.2 | 21.7 | 1.9 | 2.2 |
| 0.08 | 23.2 | 1.1 | 1.5 | 21.7 | 1.8 | 2.3 |
| 0.09 | 22.2 | 2.1 | 1.5 | 22 | 1.5 | 2.3 |
| 0.1 | 231.5 | 1.3 | 20.4 | 2.5 | 2.9 | |
對於PNN,需要用戶設置的唯一未知參數是σ,它表示有效的高斯窗的寬度。用10重交叉驗證技術確定。結果如下表。可見,對於(t-2)和(t-3)年數據,σ = 1時PNN的平均效果都是最好
PNN參數σ的lO重交叉驗證分析
| σ | (t-2) | (t-3) | ||||
|---|---|---|---|---|---|---|
| 總正確數 | 一類錯誤數 | 二類錯誤數 | 總正確數 | 一類錯誤數 | 二類錯誤數 | |
| 1 | 23.2 | 1.2 | 1.4 | 21.4 | 1.7 | 2.7 |
| 2 | 22.5 | 1.6 | 1.7 | 19.7 | 2.3 | 3.8 |
| 3 | 22.1 | 2 | 1.7 | 19.3 | 2.7 | 3.8 |
LVQ的學習速率飲由lO重交叉驗證確定,結果如下表。可見,當學習速率LR=0.05時(t-2)年模型平均效果最好;當LR=0.01時(t-3)年模型平均效果最好。
LVQ學習速率10重交叉驗證分析
| LR | (t-2) | (t-3) | ||||
|---|---|---|---|---|---|---|
| 總正確數 | 一類錯誤數 | 二類錯誤數 | 總正確數 | 一類錯誤數 | 二類錯誤數 | |
| 0.005 | 22.1 | 1.9 | 1.8 | 19.2 | 2.8 | 3.8 |
| 0.01 | 22 | 2 | 1.8 | 19.3 | 2.7 | 3.8 |
| 0.05 | 22.3 | 1.9 | 1.6 | 18.9 | 2.8 | 4.1 |
| 0.1 | 22 | 1.8 | 2 | 19.2 | 2.4 | 4.2 |
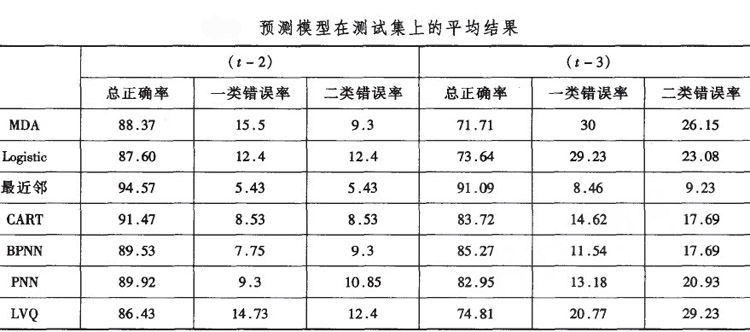
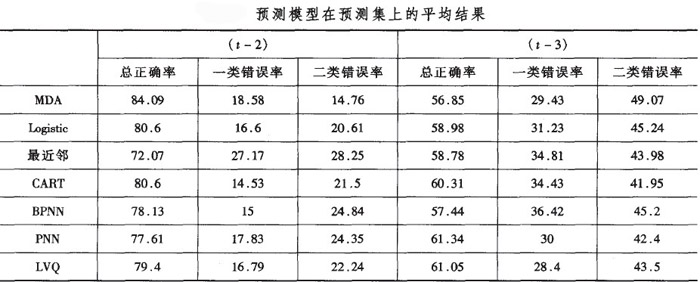
分別採用在預測集和測試集上的10次分類結果的平均值來進行比較。具體是,在模型選擇時所用的10重交叉訓練集上確立10個具體分類模型,然後分別在相應的10個交叉測試集和同一預測集上進行分類,將分別得到的10個分類結果進行平均。表8列出了各個模型在測試集上的平均結果,表9列出了各模型在預測集上的平均結果。
由上表和下表中的實證結果可見:
1)對於提前兩年預測,統計和神經網路模型都能有效的預測財務困境發生,其中MDA總正確率最高,最近鄰效果最差,CART和lJ09istic回歸略好於三種神經網路模型。對於提前三年預測,所有模型的預測準確率都較低,除BPNN外,其它兩種神經網路模型均優於統計模型。
2)對於提前兩年和提前三年預測,所有模型在測試集上的分類結果明顯地優於在預測集上的結果,這證明瞭用同一財務年度區間內的樣本集作為測試集,即使測試集獨立於訓練集,實證結果也趨於樂觀。
更重要的是,在測試集上效果好的模型在預測集上的效果未必好,如最近鄰模型在測試集上效果最好,而在預測集上較差。這更加表明在測試集上評價模型的不合理性。
中國上市公司作為研究對象,以因財務狀況異常而被特別處理作為界定上市公司陷入財務困境的標誌,採用交叉驗證技術建立統計和神經網路預測模型,併在獨立的預測集上進行比較。實證結果表明統計和神經網路模型都能有效地預測上市公司的財務困境,統計模型在提前兩年預測時效果較好,神經網路模型在提前三年預測時效果較好。實證結果同時表明,與訓練集處在同一財務年度區間內的測試集不能夠正確地評估模型性能。
- ↑ 謝紀剛,裘正定,韓彥俊等.上市公司財務困境預測模型比較研究[J].系統工程理論與實踐,2005,25(9)









太深奧了