線性概率模型
出自 MBA智库百科(https://wiki.mbalib.com/)
線性概率模型(Linear Prability Model)
目錄 |
線性概率模型的概述[1]
線性概率模型的命名是由於它的預測性;在自變數的值可用概率來解釋時,應變數能以此概率假定值的單位。這種模型,在其中應變數是一個虛設變數或雙值變數,並用一個或一個以上的自變數的線性函數來表示。該種模型有助於質的現象的分析。
線性概率模型是使用諸如會計比率之類的歷史數據作為模型的輸入數據,來解釋以前的貸款償還情況。我們可以使用在過去貸款償還中起重要作用的一些因素來預測新貸款的償還概率。
過去的貸款通常劃分為兩類,即違約的(Zi=1)和不違約的(Zi=0)。然後,我們通過對隨機變數(Xij)的線性回歸來進行估計,Xij表示第j個借款者的數量信息,如財務杠桿或收益率,通過如下形式的線性回歸來估算模型:
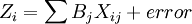
式中,Bj 表示在過去的償還情況中第j個變數的重要性。
如果我們得到變數j的估計Bj值,並且將其與對未來借款者所觀測到的Xij值相乘,併進行加總,得到借款者違約的概率E(Zi)=(1一Pi)=預期的違約率,其中Pi是對貸款償還的概率。
只要可以獲得借款者Xij的當前信息,這種方法是非常直截了當的。
該模型存在的一個最大問題是計算的Z值可能不在1和0之間。為此,指數模型對此進行了簡單的修正。把Z值代人以下公式,計算Z的指數轉化值。轉換後的值位於1和0之間。
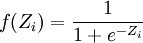
- ↑ 王愛儉.中國社區銀行發展模式研究. 中國金融出版社, 2005.12.








請問應變數是什麼?不太懂