評分者信度
出自 MBA智库百科(https://wiki.mbalib.com/)
評分者信度（scorer reliability）
目錄 |
評分者信度，指的是多個評分者給同一批人的答卷評分的一致性程度。在由客觀性試題組成的心理測驗中，答案具體而固定，無需考察評分者信度；但在投射測驗、道德判斷測驗、創造性思維測驗等測驗的評分中，答案並不固定，評分時必然摻雜有主觀判斷因素，因此在評定這些主觀性題目時，評分者之間的變異是產生誤差的重要原因之一。因此，需要考察評分者信度。
1）重測信度、複本信度和分半信度的評估方式都適用於客觀測驗，即分數評定完全客觀化的測驗。然而，當測驗評分不是那麼客觀時，還可以使用其它信度方式。例如，對於同一篇作文，不同的評定者傾向於給不同的分數，或者不同的面試官可能會在結構化面試中將同一個面試者評定為不同的分數等級。在這種情況下，可以通過運用皮爾遜積矩相關或等級相關來計算兩個評定者之間的相關而得到信度值。這種信度評估方式被稱為評定者信度或評分者信度(inter-rater reliability）。[1]
2）在由客觀性試題組成的心理測驗中，答案具體而固定，無需考察評分者信度。但在投射測驗、道德判斷測驗、創造性思維測驗等測驗的評分中，答案並不固定，評分時必然摻雜有主觀判斷因素，因此，需要考察評分者一致性繫數。[2]
3）標準化測驗一般都有較為嚴格的評分程式。對於客觀性試題來說，評分所引起的誤差可以忽略不計，但對於一些主觀性題目來說，評分者之間的變異是產生誤差的重要原因之一。 1983年的一項研究顯示：從北京隨機抽取高中語文、政治、數學、物理各5份卷子複印以後到全國各省，請各地區閱卷組分別評分，其結果是不同地區、不同閱卷組、不同閱卷老師之間差異相當大，語文同一份試卷的最大差異竟達33分。[3]
4）對一些無法完全客觀記分的測驗來說，評分者之間的變異也是誤差的重要來源。比如測量創造力的發散思維測驗以及測量人格的投射測驗，在評分時都摻有主觀判斷成分。對於這類測驗，除需要通常的信度估計外，還需要評分者信度的度量。[4]
5）除非記錄錯誤，否則不同的評分者對某一個體在客觀性測驗上的計分應該是一致的。但是，對於短文或者口語測試，以及其它的評價性判斷（人格評分、投射測驗計分）而言，計分過程往往相當主觀。評價性計分包含了評分者的主觀判斷，不同的評分者在多大程度上能夠對不同的受測者和項目的反應結果在評分、或者其它數量指標上達成一致，知道這一點是非常重要的。
口語測試的信度一向不高，但如果使用一些特殊的表格來判斷口試成績，則可以提高口試的客觀性，相應地也就提高了測試的信度。雖然口試的信度相對於紙筆測驗通常要低一些，但只要在設計口試問題時多加小心，並使用多重評價或多重計分，就能提高口試得分的信度。某些研究生課程、本科生課程以及職業技校的課程中，實施口試時使用這些方法能使評分者信度繫數達到0.60~0.70。其它有關提高口試成績評價信度的建議包括：鼓勵受測者延遲作答，讓受測者能夠在回答前思考一會兒；另外就是使用電子設備錄下受測者的反應，以便計分者可以再測試後進行重放和再評價。[5]
判斷評分者信度（intercourse 或 interrater reliability）最常見的辦法就是讓兩個人對一定數量的受測者的反應結果進行計分，然後多個人同時對多個受測者的反應進行計分。最後一種辦法得到的是組內繫數（intraclass coefficient），或者稱和諧繫數（coefficient of concordance），它是更加概括化的評分者信度繫數。[5]
考察評分者信度的方法是：隨機抽取相當份數的試卷，由兩位或多位評分者按記分規則分別給分，然後根據每份試卷的分數考察評分的一致性。主要評分方法包括皮爾遜積矩相關法、斯皮爾曼等級相關法以及肯德爾和諧繫數法，一般要求在成對的受過訓練的評分者之間平均一致性達到0.90分以上，才認為評分是客觀的。
如果只有兩位評分者，計算其評分的相關係數，即得評分者信度。一般要求在成對的受過訓練的評分者之間平均一致性達到0.90分以上，才認為評分是客觀的。
當多個評分者評多位評分對象，並以等級法記分時，還可以採用肯德爾和諧繫數作為評分者信度的估計，公式如下：
![W=12\left[\sum R^2_i-\left(\sum R_i\right)^2/_N\right]/\left[K^2\left(N^3-N\right)\right]](/w/images/math/e/c/0/ec016b221d526c164e787d636c989c15.png)
其中，K是評分者人數，N是被評的對象數（通常是考生數，每個考生一份試卷），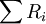
是第i個被評對象（考卷）被評的水平等級之和。
當評分者（K）為3-20人，被評對象（N）為3-7人的小樣本時，可利用肯德爾和諧繫數來考察W是否達到顯著水平。如果求得的W值大於表中所列的相應數值，就說明評分是較為一致的。
當N大於7時，則可計算X2值並作X2檢驗[X2=K(N-1)W,df-=N-1]，如果X2值達到顯著水平，則W值也算達到顯著水平。
若評分中有相同等級出現，則要使用以下公式計算求W值：
![W=12\left[\sum R^2_i-\left(\sum R_i\right)^2/_N\right]/_{\left[K^2\left(N^2-N\right)-K\sum\left(n^3-n\right)/_{12}\right]}](/w/images/math/3/e/5/3e57ff0e12a32033c4eaf0ec61090dfe.png)
其中，n為相同等級的個數，其他指標與上述公式中的指標含義相同（上述公式如下）：
