评分者信度
出自 MBA智库百科(https://wiki.mbalib.com/)
评分者信度（scorer reliability）
目录 |
评分者信度，指的是多个评分者给同一批人的答卷评分的一致性程度。在由客观性试题组成的心理测验中，答案具体而固定，无需考察评分者信度；但在投射测验、道德判断测验、创造性思维测验等测验的评分中，答案并不固定，评分时必然掺杂有主观判断因素，因此在评定这些主观性题目时，评分者之间的变异是产生误差的重要原因之一。因此，需要考察评分者信度。
1）重测信度、复本信度和分半信度的评估方式都适用于客观测验，即分数评定完全客观化的测验。然而，当测验评分不是那么客观时，还可以使用其它信度方式。例如，对于同一篇作文，不同的评定者倾向于给不同的分数，或者不同的面试官可能会在结构化面试中将同一个面试者评定为不同的分数等级。在这种情况下，可以通过运用皮尔逊积矩相关或等级相关来计算两个评定者之间的相关而得到信度值。这种信度评估方式被称为评定者信度或评分者信度(inter-rater reliability）。[1]
2）在由客观性试题组成的心理测验中，答案具体而固定，无需考察评分者信度。但在投射测验、道德判断测验、创造性思维测验等测验的评分中，答案并不固定，评分时必然掺杂有主观判断因素，因此，需要考察评分者一致性系数。[2]
3）标准化测验一般都有较为严格的评分程序。对于客观性试题来说，评分所引起的误差可以忽略不计，但对于一些主观性题目来说，评分者之间的变异是产生误差的重要原因之一。 1983年的一项研究显示：从北京随机抽取高中语文、政治、数学、物理各5份卷子复印以后到全国各省，请各地区阅卷组分别评分，其结果是不同地区、不同阅卷组、不同阅卷老师之间差异相当大，语文同一份试卷的最大差异竟达33分。[3]
4）对一些无法完全客观记分的测验来说，评分者之间的变异也是误差的重要来源。比如测量创造力的发散思维测验以及测量人格的投射测验，在评分时都掺有主观判断成分。对于这类测验，除需要通常的信度估计外，还需要评分者信度的度量。[4]
5）除非记录错误，否则不同的评分者对某一个体在客观性测验上的计分应该是一致的。但是，对于短文或者口语测试，以及其它的评价性判断（人格评分、投射测验计分）而言，计分过程往往相当主观。评价性计分包含了评分者的主观判断，不同的评分者在多大程度上能够对不同的受测者和项目的反应结果在评分、或者其它数量指标上达成一致，知道这一点是非常重要的。
口语测试的信度一向不高，但如果使用一些特殊的表格来判断口试成绩，则可以提高口试的客观性，相应地也就提高了测试的信度。虽然口试的信度相对于纸笔测验通常要低一些，但只要在设计口试问题时多加小心，并使用多重评价或多重计分，就能提高口试得分的信度。某些研究生课程、本科生课程以及职业技校的课程中，实施口试时使用这些方法能使评分者信度系数达到0.60~0.70。其它有关提高口试成绩评价信度的建议包括：鼓励受测者延迟作答，让受测者能够在回答前思考一会儿；另外就是使用电子设备录下受测者的反应，以便计分者可以再测试后进行重放和再评价。[5]
判断评分者信度（intercourse 或 interrater reliability）最常见的办法就是让两个人对一定数量的受测者的反应结果进行计分，然后多个人同时对多个受测者的反应进行计分。最后一种办法得到的是组内系数（intraclass coefficient），或者称和谐系数（coefficient of concordance），它是更加概括化的评分者信度系数。[5]
考察评分者信度的方法是：随机抽取相当份数的试卷，由两位或多位评分者按记分规则分别给分，然后根据每份试卷的分数考察评分的一致性。主要评分方法包括皮尔逊积矩相关法、斯皮尔曼等级相关法以及肯德尔和谐系数法，一般要求在成对的受过训练的评分者之间平均一致性达到0.90分以上，才认为评分是客观的。
如果只有两位评分者，计算其评分的相关系数，即得评分者信度。一般要求在成对的受过训练的评分者之间平均一致性达到0.90分以上，才认为评分是客观的。
当多个评分者评多位评分对象，并以等级法记分时，还可以采用肯德尔和谐系数作为评分者信度的估计，公式如下：
![W=12\left[\sum R^2_i-\left(\sum R_i\right)^2/_N\right]/\left[K^2\left(N^3-N\right)\right]](/w/images/math/e/c/0/ec016b221d526c164e787d636c989c15.png)
其中，K是评分者人数，N是被评的对象数（通常是考生数，每个考生一份试卷），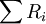
是第i个被评对象（考卷）被评的水平等级之和。
当评分者（K）为3-20人，被评对象（N）为3-7人的小样本时，可利用肯德尔和谐系数来考察W是否达到显著水平。如果求得的W值大于表中所列的相应数值，就说明评分是较为一致的。
当N大于7时，则可计算X2值并作X2检验[X2=K(N-1)W,df-=N-1]，如果X2值达到显著水平，则W值也算达到显著水平。
若评分中有相同等级出现，则要使用以下公式计算求W值：
![W=12\left[\sum R^2_i-\left(\sum R_i\right)^2/_N\right]/_{\left[K^2\left(N^2-N\right)-K\sum\left(n^3-n\right)/_{12}\right]}](/w/images/math/3/e/5/3e57ff0e12a32033c4eaf0ec61090dfe.png)
其中，n为相同等级的个数，其他指标与上述公式中的指标含义相同（上述公式如下）：
