組合預測法
出自 MBA智库百科(https://wiki.mbalib.com/)
組合預測法（Combination Forecasting）
目錄 |
組合預測方法是對同一個問題，採用兩種以上不同預測方法的預測。它既可是幾種定量方法的組合，也可是幾種定性的方法的組合，但實踐中更多的則是利用定性方法與定量方法的組合。組合的主要目的是綜合利用各種方法所提供的信息，儘可能地提高預測精度。
比如，在經濟轉軌時期，很難有一個單項預測模型能對巨集觀經濟頻繁波動的現實擬合的非常緊密並對其變動的原因作出穩定一致的解釋。理論和實踐研究都表明，在諸種單項預測模型各異且數據來源不同的情況下，組合預測模型可能導致一個比任何一個獨立預測值更好的預測值，組合預測模型能減少預測的系統誤差，顯著改進預測效果[1]。
組合預測有兩種基本形式：
1、等權組合，即各預測方法的預測值按相同的權數組合成新的預測值。
2、不等權組合，即賦予不同預測方法的預測值的權數是不一樣的。
這兩種形式的原理和運用方法完全相同，只是權數的取定上有所區別。根據已進行的預測結果，採用不等權組合的組合預測法結果較為準確。
組合預測法的原則及步驟[1]
組合預測法的應用原則以及一般步驟
1、應用原則：定性分析與定量分析相結合原則；系統性原則；經濟性原則。
2、步驟：以經濟預測為例，一般步驟是根據經濟理論和實際情況建立各種獨立的單項預測模型；運用系統聚類分析方法度量各單項模型的類間相似程度；根據聚類結果，逐層次建立組合預測模型進行預測。
組合預測模型模式一：線性組合模型；模式二：最優線性組合模型；模式三：貝葉斯組合模型；模式四：轉換函數組合模型；模式五：計量經濟與系統動力學組合模型。
案例一:組合預測法分析綠色紡織品的市場銷量[2]
一、綠色紡織品的國際地位
目前，全球紡織品和服裝的年交易總額約為4000億美元（僅次於旅游產業和信息產業，名列第三），我國占全球紡織品和服裝年交易總額的1/8，約500億美元& 中國已連續) 年保持世界最大的紡織品生產國和出口國地位，紡織品年出口額占中國出口商品總量的(30%左右，在美、歐、日所占市場份額分別是15%、15.2%和59.4%“入世”給我國紡織品出口帶來了機遇，紡織品出口配額將被取消，關稅降低，進口的棉花和其他輔料關稅的下降，有利於降低紡織品生產成本，增加市場競爭力。但當前以歐、美為代表的發達國家所構築的“綠色貿易壁壘”已成為一種新型的非關稅壁壘形式，並將成為限制我國紡織品出口的重要因素1998年某企業有一批價值100萬美元紡織品出口歐洲受阻，原因是檢測時發現布料染料中的化學成分對人體有害[3]。2002年某廠生產的30餘萬件夾克從歐洲被退回，理由是服裝拉鎖的有關金屬含量超過了歐洲標準，諸如此類例子不勝枚舉，綠色紡織品已成為國際市場的流行趨勢，不但廣受消費者的歡迎，也已成為發達國家構築非關稅壁壘，限制紡織品進口的新手段，企業如能更新觀念，研究進口國有關環保法規及相關的產品標準，生產綠色紡織品，不但能幫助企業跨過綠色貿易壁壘，還能幫助企業擴大出口量。[4]嘗試利用組合預測法分析影響綠色紡織品的市場銷量的主要因素，預測其市場銷量與發展前景。
二、組合預測法
例：我國某紡織企業為其某品牌的綠色紡織品進入歐洲某國的市場銷量進行預測! 該企業的國際銷售部除自行調查預測外，還委托目標市場國的兩家市場調研公司進行調查預測，分別得出三種不同的預測模型：
(1)Y1 = 5.1 + 0.0046X1 + 12.35X1
(2)Y2 = 8.845 + 3.234X3
(3)Y3 = 3.693 − 5.62X4 + 4.74X5
Yi—— 目標市場國的月銷量；
X1—— 目標市場國的人均月收入；
X1—— 目標市場國的綠色消費者比例；
X4—— 每月綠色廣告費用；
C—— 本公司綠色紡織品價格；
X5—— 目標市場國主要競爭對手的綠色紡織品價格。
三個預測主體根據其獨自掌握的信息，加上大家所共用的信息，分別選擇了最合適的方法對綠色紡織品的銷量進行預測，擬合出不同的最優預測模型。顯然，這些預測結果各不相同，甚至差距很大，但我們可綜合各種預測結果，進行組合優化，來分析綠色紡織品的銷量。
1.期望值法
對得出的各種預測結果計算加權算術平均數，即
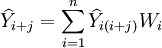
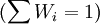
權數Wi有不同的取值方法，較常用的有：
- 等權法
取
當各種預測結果較為集中，且各種預測技術在各自信息數據條件下皆為最優模型時採用
- 擬合優度法
取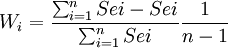
式中Sei——第i個預測模型標準誤差
當各種預測結果較分散，該模型能予以預測標準誤差最小的模型以最大的權重，使預測結果保證擬合優度
- 正態分佈法
取Wi = Ci − 1 − n − 1 / 2n − 1 式中C——組合符號
當各種預測結果排列近似於對稱分佈時，該方法使組合預測結果趨近眾多預測結果的中位數
- 組合中心法
取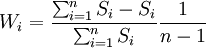
其中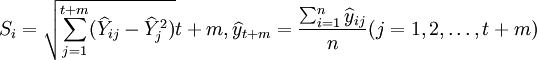
式中Si—— 第i種模型的預測結果與各種模型預測結果的均值的離差平方平均數的二次方根；
n—— 預測模型的個數；t—— 用於擬合模型的已知數據個數；
m—— 模型擬就以後所得數據的順序。
該法給予預測結果與等權組合預測結果最接近的模型以最大的權重
- 交集法
當各種預測結果為區間預測時，可取各種預測模型同一置信區間的相交區域作為組合預測的置信區間，並根據各種情況做相應處理。當各種預測結果為點預測時，組合預測置信區間通常採用第一四分位數至第三四分位數
三、組合預測法分析綠色紡織品的市場銷量
該企業以三個模型為基礎進行組合預測。已知：
X1 = 2400美元,X2 = 61%,X3 = 5萬美元,X4 = 23美元,X5 = 31美元。計算得Y1 = 23.6335,Y2 = 25.015,Y3 = 21.373。分別利用各種組合技術預測綠色紡織品的市場銷量
1.等權預測
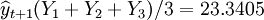(萬件)
2.擬合優度預測
已知:三種模型的標準誤分別為1.417,2.149，2.338.先計算權數得
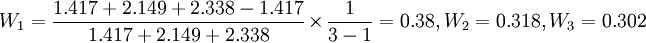
於是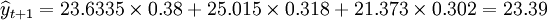
(萬件)
3.正態分佈預測
先計算權數得W_1=C^{1-1}_{3-1}/2^{3-1}=0.25,W_2=C^{2-1}_{3-1}/2^{3-1}=0.50,W_3=C^{3-1}_{3-1}/2^{3-1}=0.25
於是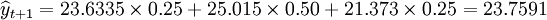
(萬件)
4.組合中心預測
已知: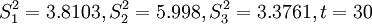
先求t+1中的Si,得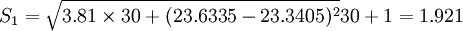
,
S2 = 2.428,S3 = 1.8418
再求權數，得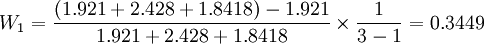
,
W2 = 0.3039,W3 = 0.3512
於是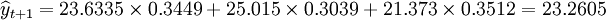
(萬件)
5.置信區間重疊預測
設取置信區間為95%，則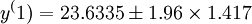
即20.8562~26.4108
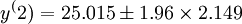
即20.703~29.227
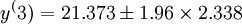
即16.7905~25.9555
於是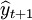
的95%的置信區間為25.955(萬件)
因此，國內紡織企業今後應加強綠色紡織品的研究，不但要提高產品質量，而且要做到知己知彼，瞭解目標市場國對綠色紡織品的需求，進行市場調研與預測+ 在市場調研與預測過程中要註意以下幾點：
(1)影響市場銷量的因素有很多，在取綠色價格、人均月收入、綠色消費者的比例、競爭對手的綠色價格為自變數擬合了三個簡單的多元線性回歸模型。現實調研中，企業往往由於經費的限制或簡單的僅以低價取勝為原則，設立的模型過於簡單，調研結果達不到理想的效果
(2)單個模型預測往往達不到理想的效果，如本文的案例中雖有三個多元線性回歸模型，但分別為三個預測主體設立，過於簡單+ 解決的辦法是擬合聯立方程組模型來較單個方程模型更全面地描述市場現象，以求更理想的預測效果，如可以考慮設立如下方程組：
生產成本=F(生產量、廣告費用、其他銷售費用)
價格=F(生產成本、普及率、市場競爭)
普及率=F(以前的銷售量、人均收入水平)
廣告費用=F(銷售量、市場競爭)
案例二:組合預測法在物流需求中的應用[5]
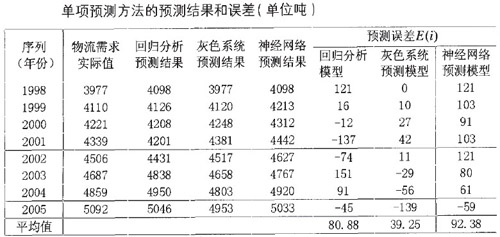
選取某物流公司物流需求量的歷史數據序列，取1998-2005年的數據為樣本，用Y1、Y2、Y3。分別代表回歸分析、灰色系統、神經網路3種不同的預測模型對物流需求進行預測，並將三種預測模型的結果與實際值進行比較計算預測誤差如表所示：
通過比較上述三種模型預測誤差絕對值的平均值，可以看到在本次物流需求中，神經網路的誤差最大，回歸分析次之，灰色模型預測的誤差最小，這正反映了各種模型在物流需求預測中的優缺點。按照上表的計算結果可得組合預測的總誤差為E=\frac{1}{3}(80.88+39.25+92.38)=70.84
根據Shapley值得概念，參與組合預測模型總誤差分攤的“合作關係”的成員為：N={1,2,3},它的所有子集的組合的誤差值分別為它的所有子集的組合的誤差值分別為E{1}、E{2}、E{3}、E{1,2}、E{1,3}、E{2,3}E{1,2,3},其數值的大小為該子集所包括向量誤差的均值大小如表2所示
表各子集的誤差值
| E{1} | E{2} | E{3} | E{1,2} | E{1,3} | E{2,3} | E{1,2,3} |
| 80.88 | 39.25 | 92.38 | 60.06 | 86.63 | 65.82 | 70.84 |
按照公式(3)，(4)的Shapley值計算方法，求各成員的Shapley值為：
![E_1=\frac{0!2!}{3!}\left[E{1}-E({1}1})\right]+\frac{1!1!}{3!}\left[E{1,2E({1,2}1})\right]+\frac{1!1!}{3!}\left[E{1,3E({1,3}1})\right]+\frac{2!0!}{3!}\left[E{1,2,3E({1,2,3}1})\right]=31.14](/w/images/math/d/1/7/d17edd90a96824c7d3dca0e14bffd12a.png)
同样可得单项预测方法y_2,y_3应当分摊的误差量为：E2 = − 0.07,E3 = 39.77。而E1 + E2 + E3 = 70.84说明三种单一预测方法分摊的误差的和等于总的误差量E，即各个方法分摊误差的计算结果正确。各分摊值的大小则说明了各自预测模型的精度的大小。根据上面的计算结果和公式(5)，计算各个预测方法在组合模型中的最终的权重为：
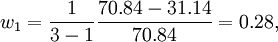
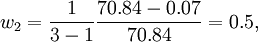
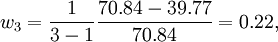
根据所得的组合权重我们可知组合预测模型为：Y=O.28+0.5+0.22。Y为组合预测模型的预测值。利用组合预测模型Y对1998-2005进行物流需求预测，并计算组合预测结果的误差及相对误差如下表所示：
表物流需求组合预测值及误差、相对误差
| 年份序列 | 1998 | 1999 | 2000 | 2001 | 2002 | 2003 | 2004 | 2005 |
| 物流需求实际值 | 3977 | 4110 | 4221 | 4339 | 4506 | 4687 | 4859 | 5092 |
| 组合预测值 | 4037.5 | 4142.1 | 4250.9 | 4344.0 | 4517.1 | 4732.3 | 4869.9 | 4996.6 |
| 组合预测误差 | 60.5 | 32.1 | 29.9 | 5.0 | 11.1 | 45.3 | 10.9 | -95.3 |
| 组合预测相对误差(％) | 1.52 | 0.78 | 0.7l | O.12 | 0.25 | 0.97 | 0.23 | -1.87 |
从上表可知：基于Shapley值法的权重分配组合预测方法模型在物流需求预测的应用中具有较好的预测能力，大部分组合预测的相对误差保持在1％之内，只有1998,2005年的相对误差超过这个范围，但也未超过2％。
可看出该权重分配法的组合预测方法在物流需求预测中能很好的达到物流需求预测的要求，并且计算过程简单，对数学基础要求不高，值得推广应用。
例子中的擬合優度法的標準誤差怎麼求呢？