稻田條件
出自 MBA智库百科(https://wiki.mbalib.com/)
稻田條件(Inada Conditions)
目錄 |
稻田條件指某種新古典生產函數,滿足:f(0)=0,一階導數大於0,二階導數小於0,另外,當生產要素投入趨於0時,一階導數的極限無窮大,當生產要素的投入趨於無窮大時,一階導數的極限等於0。
在巨集觀經濟學中,稻田條件(根據日本經濟學家稻田獻一命名)是關於生產方程形狀的假設。如果滿足稻田條件,就在新古典經濟增長模型中滿足了經濟增長穩定.
對於函數f(x),六個條件是:
1、函數 f(x) 在x為0時的值為0: f(0)=0
2、函數連續可導,
3、函數對任何自變數xi都嚴格遞增: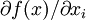 >0,
>0,
4、函數的二階導數對自變數xi嚴格遞減(也就是說函數是凹函數): 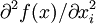 <0,
<0,
5、一階導函數在任一自變數x_{i}趨於0時極限為正無窮大: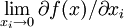 =
= ,
,
6、一階導函數在任一自變數xi趨於正無窮大時極限為0: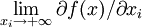 =0
=0
可以證明稻田條件決定了生產方程一定是漸進於Cobb–Douglas函數.
保證經濟的路徑不發散,對經濟均衡的穩定性存在性起著至關重要的作用。在經濟建模中,稻田條件的另一個重要應用是保證內點解的存在。如果沒有稻田條件,那麼模型的構建者需要使用外生條件來限制資本或消費大於0。如果生產函數具備稻田性質,那麼嚴格大於0的限制條件會自然滿足,進而可以在最優化的求解過程中將其忽略。
如總供給函數的推導中 Y=AF(K,L,t) 令A=1(不考慮技術的革新)K固定,則可寫成Y=F(L)
此式就符合“稻田條件”:
1.f(0)=0;
2.一階導數大於0,二階導數小於0;
3.當L趨於0時,一階導數的極限無窮大(投入的勞動力極少時引起的產出的增加量無窮大);
4.當生產要素的投入趨於無窮大時,一階導數的極限等於0(投入的勞動力無窮大,增加單位勞力增加的產出趨近於零)。








可以補充下相關文獻嗎