稻田条件

出自 MBA智库百科(https://wiki.mbalib.com/)

稻田条件(Inada Conditions)

　　稻田条件指某种新古典生产函数，满足：f（0）=0，一阶导数大于0，二阶导数小于0，另外，当生产要素投入趋于0时，一阶导数的极限无穷大，当生产要素的投入趋于无穷大时，一阶导数的极限等于0。

　　在宏观经济学中，稻田条件(根据日本经济学家稻田献一命名)是关于生产方程形状的假设。如果满足稻田条件，就在新古典经济增长模型中满足了经济增长稳定.

　　对于函数f(x)，六个条件是:

　　1、函数 f(x) 在x为0时的值为0: f(0)=0

　　2、函数连续可导,

　　3、函数对任何自变量x_i都严格递增: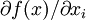>0,

　　4、函数的二阶导数对自变量x_i严格递减(也就是说函数是凹函数): 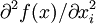<0,

　　5、一阶导函数在任一自变量x_{i}趋于0时极限为正无穷大： =,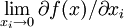

　　6、一阶导函数在任一自变量x_i趋于正无穷大时极限为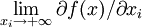0： =0

　　可以证明稻田条件决定了生产方程一定是渐进于Cobb–Douglas函数.

　　保证经济的路径不发散，对经济均衡的稳定性存在性起着至关重要的作用。在经济建模中，稻田条件的另一个重要应用是保证内点解的存在。如果没有稻田条件，那么模型的构建者需要使用外生条件来限制资本或消费大于0。如果生产函数具备稻田性质，那么严格大于0的限制条件会自然满足，进而可以在最优化的求解过程中将其忽略。

　　如总供给函数的推导中 Y=AF(K,L,t) 令A=1（不考虑技术的革新）K固定，则可写成Y=F(L)

　　此式就符合“稻田条件”：

　　1.f(0)=0；

　　2.一阶导数大于0，二阶导数小于0；

　　3.当L趋于0时，一阶导数的极限无穷大（投入的劳动力极少时引起的产出的增加量无穷大）；

　　4.当生产要素的投入趋于无穷大时，一阶导数的极限等于0（投入的劳动力无穷大，增加单位劳力增加的产出趋近于零）。