全球专业中文经管百科，由121,994位网友共同编写而成，共计435,874个条目

查看

工具▼

直線趨勢模型預測法

用手机看条目

出自 MBA智库百科(https://wiki.mbalib.com/)

目錄

1 什麼是直線趨勢模型預測法
2 直線趨勢預測模型[1]
3 直線趨勢模型預測法實例分析
4 相關條目
5 參考文獻

什麼是直線趨勢模型預測法

　　直線趨勢模型預測法是利用描述預測對象的直線趨勢模型進行外推預測的方法。在統計預測中，當某一變數的時間序列在長時期內呈連續增長或減少的變動趨勢，且其逐期增減量大致相同時，常用直線趨勢模型進行預測。

直線趨勢預測模型^[1]

　　直線趨勢預測模型為：

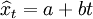
　　 $\widehat{x}_t=a+bt$

　　式中，a,b為趨勢模型待定的兩個參數，t代表時間。

　　利用數據(t,x_t),t=1、2、…、n，根據最小平方法可得參數a、b的估計為下列標準方程組的解

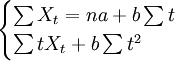
　　 $\begin{cases}\sum X_t=na+b\sum t\\\sum t X_t+b\sum t^2\end{cases}$

　　估計出a、b的值以後就可以進行預測。

　　其預測標準誤差為：

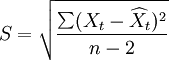
　　 $S=\sqrt{\frac{\sum(X_t-\widehat{X}_t)^2}{n-2}}$

直線趨勢模型預測法實例分析

　　某企業連續9年的銷售額如下，試預測2002年的銷售額。

年份	時間t	銷售額 $X t$	$t 2$	$t X t$	預測值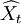 $\widehat{X}_t$	預測誤差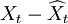 $X_t-\widehat{X}_t$	預測誤差平方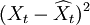 $(X_t-\widehat{X}_t)^2$
1993	-4	300	16	-1200	299.16	0.84	0.7056
1995	-3	324	9	-972	323.51	0.49	0.2401
1996	-1	372	1	-372	372.21	-0.21	0.0441
1997	0	396	0	0	396.56	-0.56	0.3136
1998	1	420	1	420	420.91	-0.91	0.8281
1999	2	446	4	892	445.26	0.74	0.5476
2000	3	469	9	1407	469.61	-0.61	0.3721
2001	4	495	16	1980	493.96	-0.06	1.0816
合計	-	3569	60	1461	-	-	4.8724

　　根據給定時間序列定出時間t的值代入表中第二列，則

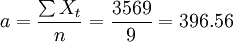
　　 $a=\frac{\sum X_t}{n}=\frac{3569}{9}=396.56$

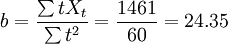
　　 $b=\frac{\sum tX_t}{\sum t^2}=\frac{1461}{60}=24.35$

　　其直線趨勢預測模型為：

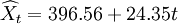
　　 $\widehat{X}_t=396.56+24.35t$

　　預測2002年的銷售額，取t=5,則

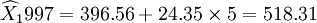　　 $\widehat{X}_1997=396.56+24.35\times5=518.31$ (萬元)

　　其預測標準誤差為：

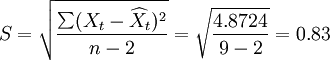
　　 $S=\sqrt{\frac{\sum(X_t-\widehat{X}_t)^2}{n-2}}=\sqrt{\frac{4.8724}{9-2}}=0.83$

相關條目

參考文獻

↑ 馬樹才主編.統計學教程[M].ISBN:978-7-5610-3730-0/F568.遼寧大學出版社,2002.06

取自"https://wiki.mbalib.com/zh-tw/%E7%9B%B4%E7%BA%BF%E8%B6%8B%E5%8A%BF%E6%A8%A1%E5%9E%8B%E9%A2%84%E6%B5%8B%E6%B3%95"

打开MBA智库App, 阅读完整内容打开App

如果您認為本條目還有待完善，需要補充新內容或修改錯誤內容，請編輯條目或投訴舉報。

本条目由以下用户参与贡献

頁面分類: 決策方法

評論(共3條)

提示:評論內容為網友針對條目"直線趨勢模型預測法"展開的討論，與本站觀點立場無關。

61.227.90.* 在 2021年3月10日 11:06 發表

趨勢模型預測的例子寫錯了，時間合計不是0?

回複評論

Llyn (討論 | 貢獻) 在 2021年3月10日 13:37 發表

61.227.90.* 在 2021年3月10日 11:06 發表

趨勢模型預測的例子寫錯了，時間合計不是0?

謝謝指正，已修改

回複評論

116.20.67.* 在 2022年3月10日 11:09 發表

例子里的數據少了1994這一年的數據，說是9年，實際只有8條數據

回複評論

發表評論請文明上網，理性發言並遵守有關規定。

以上内容根据网友推荐自动排序生成

闽公网安备 35020302032707号