全球专业中文经管百科，由121,994位网友共同编写而成，共计435,879个条目

查看

工具箱▼

直线趋势模型预测法

用手机看条目

出自 MBA智库百科(https://wiki.mbalib.com/)

目录

1 什么是直线趋势模型预测法
2 直线趋势预测模型[1]
3 直线趋势模型预测法实例分析
4 相关条目
5 参考文献

什么是直线趋势模型预测法

　　直线趋势模型预测法是利用描述预测对象的直线趋势模型进行外推预测的方法。在统计预测中，当某一变量的时间序列在长时期内呈连续增长或减少的变动趋势，且其逐期增减量大致相同时，常用直线趋势模型进行预测。

直线趋势预测模型^[1]

　　直线趋势预测模型为：

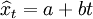
　　 $\widehat{x}_t=a+bt$

　　式中，a,b为趋势模型待定的两个参数，t代表时间。

　　利用数据(t,x_t),t=1、2、…、n，根据最小平方法可得参数a、b的估计为下列标准方程组的解

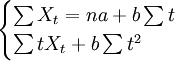
　　 $\begin{cases}\sum X_t=na+b\sum t\\\sum t X_t+b\sum t^2\end{cases}$

　　估计出a、b的值以后就可以进行预测。

　　其预测标准误差为：

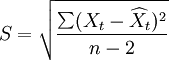
　　 $S=\sqrt{\frac{\sum(X_t-\widehat{X}_t)^2}{n-2}}$

直线趋势模型预测法实例分析

　　某企业连续9年的销售额如下，试预测2002年的销售额。

年份	时间t	销售额 $X t$	$t 2$	$t X t$	预测值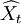 $\widehat{X}_t$	预测误差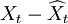 $X_t-\widehat{X}_t$	预测误差平方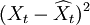 $(X_t-\widehat{X}_t)^2$
1993	-4	300	16	-1200	299.16	0.84	0.7056
1995	-3	324	9	-972	323.51	0.49	0.2401
1996	-1	372	1	-372	372.21	-0.21	0.0441
1997	0	396	0	0	396.56	-0.56	0.3136
1998	1	420	1	420	420.91	-0.91	0.8281
1999	2	446	4	892	445.26	0.74	0.5476
2000	3	469	9	1407	469.61	-0.61	0.3721
2001	4	495	16	1980	493.96	-0.06	1.0816
合计	-	3569	60	1461	-	-	4.8724

　　根据给定时间序列定出时间t的值代入表中第二列，则

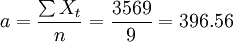
　　 $a=\frac{\sum X_t}{n}=\frac{3569}{9}=396.56$

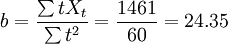
　　 $b=\frac{\sum tX_t}{\sum t^2}=\frac{1461}{60}=24.35$

　　其直线趋势预测模型为：

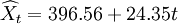
　　 $\widehat{X}_t=396.56+24.35t$

　　预测2002年的销售额，取t=5,则

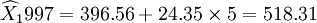　　 $\widehat{X}_1997=396.56+24.35\times5=518.31$ (万元)

　　其预测标准误差为：

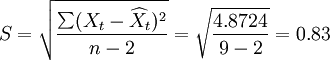
　　 $S=\sqrt{\frac{\sum(X_t-\widehat{X}_t)^2}{n-2}}=\sqrt{\frac{4.8724}{9-2}}=0.83$

相关条目

参考文献

↑ 马树才主编.统计学教程[M].ISBN:978-7-5610-3730-0/F568.辽宁大学出版社,2002.06

来自"https://wiki.mbalib.com/wiki/%E7%9B%B4%E7%BA%BF%E8%B6%8B%E5%8A%BF%E6%A8%A1%E5%9E%8B%E9%A2%84%E6%B5%8B%E6%B3%95"

打开MBA智库App, 阅读完整内容打开App

如果您认为本条目还有待完善，需要补充新内容或修改错误内容，请编辑条目或投诉举报。

本条目由以下用户参与贡献

页面分类: 决策方法

评论(共3条)

提示:评论内容为网友针对条目"直线趋势模型预测法"展开的讨论，与本站观点立场无关。

61.227.90.* 在 2021年3月10日 11:06 发表

趨勢模型預測的例子寫錯了，時間合計不是0?

回复评论

Llyn (Talk | 贡献) 在 2021年3月10日 13:37 发表

61.227.90.* 在 2021年3月10日 11:06 发表

趨勢模型預測的例子寫錯了，時間合計不是0?

谢谢指正，已修改

回复评论

116.20.67.* 在 2022年3月10日 11:09 发表

例子里的数据少了1994这一年的数据，说是9年，实际只有8条数据

回复评论

发表评论请文明上网，理性发言并遵守有关规定。

以上内容根据网友推荐自动排序生成

闽公网安备 35020302032707号