柯西分佈
用手机看条目
出自 MBA智库百科(https://wiki.mbalib.com/)
柯西分佈(Cauchy distribution)
目錄 |
[編輯]
柯西分佈也叫柯西-洛倫茲分佈，它是以奧古斯丁·路易·柯西與亨德里克·洛倫茲名字命名的連續概率分佈，其概率密度函數為：
![f(x;x_0,\gamma)=\frac{1}{\pi\gamma[1+(\frac{x-x_0}{\gamma})^2]}=\frac{1}{\pi}[\frac{\gamma}{(x-x_0)^2+\gamma^2}]](/w/images/math/6/2/e/62e2720c75226315ab9f08e920d37e38.png)
X0是定義分佈峰值位置的位置參數,γ是最大值一半處的一半寬度的尺度參數。
作為概率分佈，通常叫作柯西分佈，物理學家也將之稱為洛倫茲分佈或者Breit-Wigner分佈 。在物理學中的重要性很大一部分歸因於它是描述受迫共振的微分方程的解。在光譜學中，它描述了被共振或者其它機制加寬的譜線形狀。在下麵的部分將使用柯西分佈這個統計學術語。
[編輯]
其累積分佈函數為：
柯西分佈的逆累積分佈函數為
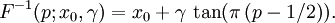
柯西分佈的平均值、方差或者矩都沒有定義，它的眾數與中值有定義都等於 x0。
取 X 表示柯西分佈隨機變數，柯西分佈的特性函數表示為：
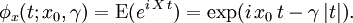
如果 U 與 V 是期望值為 0、方差為 1 的兩個獨立正態分佈隨機變數的話，那麼比值 U/V 為柯西分佈。
如果 X1, …, Xn 是分別符合柯西分佈的相互獨立同分佈隨機變數，那麼算術平均數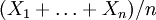
有同樣的柯西分佈。為了證明這一點，我們來計算採樣平均的特性函數：
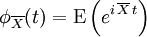
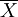是採樣平均值。這個例子表明不能捨棄
很好@@@@