層次分析法
出自 MBA智库百科(https://wiki.mbalib.com/)
層次分析法(The analytic hierarchy process,簡稱AHP),也稱層級分析法
目錄 |
層次分析法(The analytic hierarchy process)簡稱AHP,在20世紀70年代中期由美國運籌學家托馬斯·塞蒂(T.L.saaty)正式提出。它是一種定性和定量相結合的、系統化、層次化的分析方法。由於它在處理複雜的決策問題上的實用性和有效性,很快在世界範圍得到重視。它的應用已遍及經濟計劃和管理、能源政策和分配、行為科學、軍事指揮、運輸、農業、教育、人才、醫療和環境等領域。
層次分析法的基本思路與人對一個複雜的決策問題的思維、判斷過程大體上是一樣的。不妨用假期旅游為例:假如有3個旅游勝地A、B、C供你選擇,你會根據諸如景色、費用和居住、飲食、旅途條件等一些準則去反覆比較這3個候選地點.首先,你會確定這些準則在你的心目中各占多大比重,如果你經濟寬綽、醉心旅游,自然分別看重景色條件,而平素儉樸或手頭拮据的人則會優先考慮費用,中老年旅游者還會對居住、飲食等條件寄以較大關註。其次,你會就每一個準則將3個地點進行對比,譬如A景色最好,B次之;B費用最低,C次之;C居住等條件較好等等。最後,你要將這兩個層次的比較判斷進行綜合,在A、B、C中確定哪個作為最佳地點。
1、建立層次結構模型。在深入分析實際問題的基礎上,將有關的各個因素按照不同屬性自上而下地分解成若幹層次,同一層的諸因素從屬於上一層的因素或對上層因素有影響,同時又支配下一層的因素或受到下層因素的作用。最上層為目標層,通常只有1個因素,最下層通常為方案或對象層,中間可以有一個或幾個層次,通常為準則或指標層。當準則過多時(譬如多於9個)應進一步分解出子準則層。
2、構造成對比較陣。從層次結構模型的第2層開始,對於從屬於(或影響)上一層每個因素的同一層諸因素,用成對比較法和1—9比較尺度構造成對比較陣,直到最下層。
3、計算權向量並做一致性檢驗。對於每一個成對比較陣計算最大特征根及對應特征向量,利用一致性指標、隨機一致性指標和一致性比率做一致性檢驗。若檢驗通過,特征向量(歸一化後)即為權向量:若不通過,需重新構造成對比較陣。
4、計算組合權向量並做組合一致性檢驗。計算最下層對目標的組合權向量,並根據公式做組合一致性檢驗,若檢驗通過,則可按照組合權向量表示的結果進行決策,否則需要重新考慮模型或重新構造那些一致性比率較大的成對比較陣。
運用層次分析法有很多優點,其中最重要的一點就是簡單明瞭。層次分析法不僅適用於存在不確定性和主觀信息的情況,還允許以合乎邏輯的方式運用經驗、洞察力和直覺。也許層次分析法最大的優點是提出了層次本身,它使得買方能夠認真地考慮和衡量指標的相對重要性。
將問題包含的因素分層:最高層(解決問題的目的);中間層(選擇為實現總目標而採取的各種措施、方案所必須遵循的準則。也可稱策略層、約束層、準則層等);最低層(用於解決問題的各種措施、方案等)。把各種所要考慮的因素放在適當的層次內。用層次結構圖清晰地表達這些因素的關係。
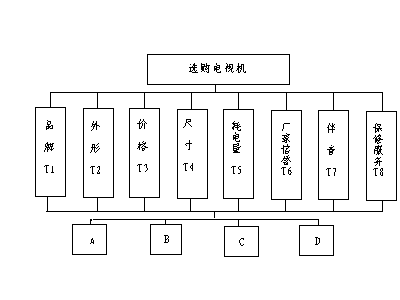
〔例1〕 購物模型
某一個顧客選購電視機時,對市場正在出售的四種電視機考慮了八項準則作為評估依據,建立層次分析模型如下:
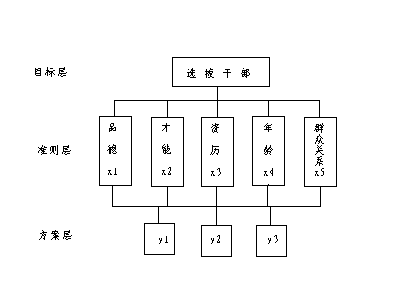
〔例2〕 選拔幹部模型
對三個幹部候選人y1、y2 、y3,按選拔幹部的五個標準:品德、才能、資歷、年齡和群眾關係,構成如下層次分析模型: 假設有三個幹部候選人y1、y2 、y3,按選拔幹部的五個標準:品德,才能,資歷,年齡和群眾關係,構成如下層次分析模型
比較第 i 個元素與第 j 個元素相對上一層某個因素的重要性時,使用數量化的相對權重aij來描述。設共有 n 個元素參與比較,則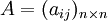 稱為成對比較矩陣。
稱為成對比較矩陣。
成對比較矩陣中aij的取值可參考 Satty 的提議,按下述標度進行賦值。aij在 1-9 及其倒數中間取值。
- aij = 1,元素 i 與元素 j 對上一層次因素的重要性相同;
- aij = 3,元素 i 比元素 j 略重要;
- aij = 5,元素 i 比元素 j 重要;
- aij = 7, 元素 i 比元素 j 重要得多;
- aij = 9,元素 i 比元素 j 的極其重要;
- aij = 2n,n=1,2,3,4,元素 i 與 j 的重要性介於aij = 2n − 1與aij = 2n + 1之間;
-
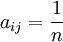 ,n=1,2,...,9, 當且僅當aji = n。
,n=1,2,...,9, 當且僅當aji = n。
成對比較矩陣的特點: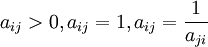 。(備註:當i=j時候,aij = 1)
。(備註:當i=j時候,aij = 1)
對例 2, 選拔幹部考慮5個條件:品德x1,才能x2,資歷x3,年齡x4,群眾關係x5。某決策人用成對比較法,得到成對比較陣如下:
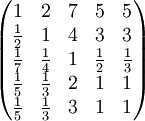
a14 = 5 表示品德與年齡重要性之比為 5,即決策人認為品德比年齡重要。
從理論上分析得到:如果A是完全一致的成對比較矩陣,應該有
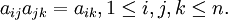
但實際上在構造成對比較矩陣時要求滿足上述眾多等式是不可能的。因此退而要求成對比較矩陣有一定的一致性,即可以允許成對比較矩陣存在一定程度的不一致性。
由分析可知,對完全一致的成對比較矩陣,其絕對值最大的特征值等於該矩陣的維數。對成對比較矩陣 的一致性要求,轉化為要求: 的絕對值最大的特征值和該矩陣的維數相差不大。
檢驗成對比較矩陣A一致性的步驟如下:
- 計算衡量一個成對比較矩陣 A (n>1 階方陣)不一致程度的指標CI:
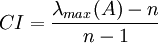
RI是這樣得到的:對於固定的n,隨機構造成對比較陣A, 其中aij是從1,2,…,9,1/2,1/3,…,1/9中隨機抽取的. 這樣的A是不一致的, 取充分大的子樣得到A的最大特征值的平均值
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| RI | 0 | 0 | 0.58 | 0.90 | 1.12 | 1.24 | 1.32 | 1.41 | 1.45 |
註解:
- 從有關資料查出檢驗成對比較矩陣 A 一致性的標準RI:RI稱為平均隨機一致性指標,它只與矩陣階數 n 有關。
- 按下麵公式計算成對比較陣 A 的隨機一致性比率 CR:
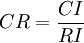 。
。
- 判斷方法如下: 當CR<0.1時,判定成對比較陣 A 具有滿意的一致性,或其不一致程度是可以接受的;否則就調整成對比較矩陣 A,直到達到滿意的一致性為止。
例如對例 2 的矩陣
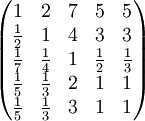
計算得到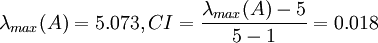 ,查得RI=1.12,
,查得RI=1.12,
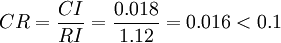
這說明 A 不是一致陣,但 A 具有滿意的一致性,A 的不一致程度是可接受的。
此時A的最大特征值對應的特征向量為U=(-0.8409,-0.4658,-0.0951,-0.1733,-0.1920)。 這個向量也是問題所需要的。通常要將該向量標準化:使得它的各分量都大於零,各分量之和等於 1。該特征向量標準化後變成U = (0.475,0.263,0.051,0.103,0.126)Z。經過標準化後這個向量稱為權向量。這裡它反映了決策者選拔幹部時,視品德條件最重要,其次是才能,再次是群眾關係,年齡因素,最後才是資歷。各因素的相對重要性由權向量U的各分量所確定。
求A的特征值的方法,可以用 MATLAB 語句求A的特征值:〔Y,D〕=eig(A),D為成對比較陣 的特征值,Y的列為相應特征向量。
在實踐中,可採用下述方法計算對成對比較陣A = (aij)的最大特征值λmax(A)和相應特征向量的近似值。
定義
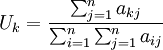 ,
,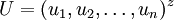
可以近似地看作A的對應於最大特征值的特征向量。
計算
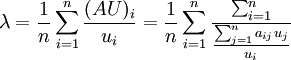
可以近似看作A的最大特征值。實踐中可以由λ來判斷矩陣A的一致性。
現在來完整地解決例 2 的問題,要從三個候選人y1,y2,y3中選一個總體上最適合上述五個條件的候選人。對此,對三個候選人y = y1,y2,y3分別比較他們的品德(x1),才能(x2),資歷(x3),年齡(x4),群眾關係(x5)。
先成對比較三個候選人的品德,得成對比較陣
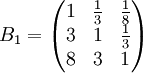
經計算,B1的權向量
ωx1(Y) = (0.082,0.236,0.682)z
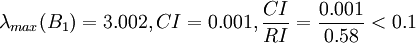
故B1的不一致程度可接受。ωx1(Y)可以直觀地視為各候選人在品德方面的得分。
類似地,分別比較三個候選人的才能,資歷,年齡,群眾關係得成對比較陣
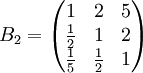
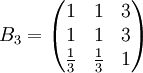
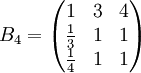
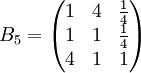
通過計算知,相應的權向量為
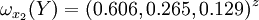
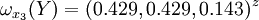
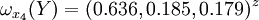
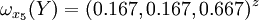
它們可分別視為各候選人的才能分,資歷分,年齡分和群眾關係分。經檢驗知B2,B3,B4,B5的不一致程度均可接受。
最後計算各候選人的總得分。y1的總得分
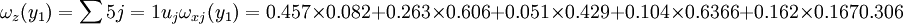
從計算公式可知,y1的總得分ω(y1)實際上是y1各條件得分ωx1(y1) ,ωx2(y1) ,...,ωx5(y1) ,的加權平均, 權就是各條件的重要性。同理可得y2,Y3 的得分為
ωz(y2) = 0.243,ωz(y3) = 0.452
| 0.457 | 0.263 | 0.051 | 0.103 | 0.126 | 總得分 | |
| Y1 | 0.082 | 0.606 | 0.429 | 0.636 | 0.167 | 0.305 |
| Y2 | 0.244 | 0.265 | 0.429 | 0.185 | 0.167 | 0.243 |
| Y3 | 0.674 | 0.129 | 0.143 | 0.179 | 0.667 | 0.452 |
即排名:Y3 > Y1 > Y2
比較後可得:候選人y3是第一干部人選。
例如,某人準備選購一臺電冰箱,他對市場上的6種不同類型的電冰箱進行瞭解後,在決定買那一款式時,往往不是直接拿電冰箱整體進行比較,因為存在許多不可比的因素,而是選取一些中間指標進行考察。例如電冰箱的容量、製冷級別、價格、型號、耗電量、外界信譽、售後服務等。然後再考慮各種型號冰箱在上述各中間標準下的優劣排序。藉助這種排序,最終作出選購決策。在決策時,由於6種電冰箱對於每個中間標準的優劣排序一般是不一致的,因此,決策者首先要對這7個標準的重要度作一個估計,給出一種排序,然後把6種冰箱分別對每一個標準的排序權重找出來,最後把這些信息數據綜合,得到針對總目標即購買電冰箱的排序權重。有了這個權重向量,決策就很容易了。
運用AHP法進行決策時,需要經歷以下5個步驟:
1、建立系統的遞階層次結構;
2、構造兩兩比較判斷矩陣;(正互反矩陣)
3、針對某一個標準,計算各備選元素的權重;
4、計算當前一層元素關於總目標的排序權重。
5、進行一致性檢驗。
如果所選的要素不合理,其含義混淆不清,或要素間的關係不正確,都會降低AHP法的結果質量,甚至導致AHP法決策失敗。
為保證遞階層次結構的合理性,需把握以下原則:
1、分解簡化問題時把握主要因素,不漏不多;
2、註意相比較元素之間的強度關係,相差太懸殊的要素不能在同一層次比較。
1、建立遞階層次結構;
2、構造兩兩比較判斷矩陣;(正互反矩陣)
對各指標之間進行兩兩對比之後,然後按9分位比率排定各評價指標的相對優劣順序,依次構造出評價指標的判斷矩陣。
3、針對某一個標準,計算各備選元素的權重;
關於判斷矩陣權重計算的方法有兩種,即幾何平均法(根法)和規範列平均法(和法)。
(1)幾何平均法(根法)
計算判斷矩陣A各行各個元素mi的乘積;
計算mi的n次方根;
對向量進行歸一化處理;
該向量即為所求權重向量。
(2)規範列平均法(和法)
計算判斷矩陣A各行各個元素mi的和;
將A的各行元素的和進行歸一化;
該向量即為所求權重向量。
計算矩陣A的最大特征值?max
對於任意的i=1,2,…,n, 式中為向量AW的第i個元素
(4)一致性檢驗
構造好判斷矩陣後,需要根據判斷矩陣計算針對某一准則層各元素的相對權重,併進行一致性檢驗。雖然在構造判斷矩陣A時並不要求判斷具有一致性,但判斷偏離一致性過大也是不允許的。因此需要對判斷矩陣A進行一致性檢驗。
本条目由以下用户参与贡献
村姑,funwmy,苦行者,Vulture,Zfj3000,Lolo,001,Angle Roh,18°@鷺島,Mathfei,Jiejie,Cabbage,刘永祥,Yixi,Yutian85,快乐的风,Luckyxia0703,Freeheart,陈蹊,Ywlshuwei,Dan,阿南,y桑,chonglie,卢晔,LuyinT,spiitfrie,M id c23aeccbd78f69e05067a552d39e7ef8.評論(共54條)
謝謝,已更正。
能不能給出一些運用AHP的例子呢?謝謝
現已給某一購房者的情況為例,望指教。
舉出的實例,數據有誤,請作者是否考慮交驗一下。
因該條目為網友貢獻,無法獲知其出處,已對其內容進行了更改,感謝您的指正,MBA智庫百科是可以自由編輯的,您也可以直接參与編輯修改。
超過9階RI表能否提供 急需 謝謝
9 10 11 12 13 14 15
1.45 1.49 1.51 1.48 1.56 1.57 1.58
不好意思,上邊 表格沒處理好
實際上這個方法使用簡單的數學知識就可以完全說明白,裡面比較複雜的就是開平方,其它的就是加減乘除找平均數啥的。
國外的MBA教程上,都是使用最簡單的方法在教原理和過程,實在搞不明白國內的教程為什麼一定要用這些看起來很高深的東西。。。。
明顯有錯誤!
MBA智庫是可以自由編輯的,有誤之處期待您的參與完善,或者您指出錯誤之處,以便完善。
實際上這個方法使用簡單的數學知識就可以完全說明白,裡面比較複雜的就是開平方,其它的就是加減乘除找平均數啥的。
國外的MBA教程上,都是使用最簡單的方法在教原理和過程,實在搞不明白國內的教程為什麼一定要用這些看起來很高深的東西。。。。
我覺得一看就懂 只要線性代數還記得的話。。。
到底是satty教授還是saaty教授啊???
是T.L.Saaty
請問最大特征根怎麼求得?謝謝!
用matlab可以直接求得
實際上這個方法使用簡單的數學知識就可以完全說明白,裡面比較複雜的就是開平方,其它的就是加減乘除找平均數啥的。
國外的MBA教程上,都是使用最簡單的方法在教原理和過程,實在搞不明白國內的教程為什麼一定要用這些看起來很高深的東西。。。。
這個方法很簡單啊
謝謝指正,原文已修正!~
求最大特征值只需要先列向量求和歸一,求出特征向量,然後通過歸一後向量與特征向量的對應比的平均數,得出近似最大特征值(與精確值相差很小)。
特征值的求法課利用mathematica軟體:利用函數Eigenvalues[N[{{},{},{},...}]]便可求出
%層次分析法的matlab程式 disp('請輸入判斷矩陣A(n階)'); A=input('A='); [n,n]=size(A); x=ones(n,100); y=ones(n,100); m=zeros(1,100); m(1)=max(x(:,1)); y(:,1)=x(:,1); x(:,2)=A*y(:,1); m(2)=max(x(:,2)); y(:,2)=x(:,2)/m(2); p=0.0001;i=2;k=abs(m(2)-m(1)); while k>p i=i+1; x(:,i)=A*y(:,i-1); m(i)=max(x(:,i)); y(:,i)=x(:,i)/m(i); k=abs(m(i)-m(i-1)); end a=sum(y(:,i)); w=y(:,i)/a; t=m(i); disp('權向量');disp(w); disp('最大特征值');disp(t); %以下是一致性檢驗 CI=(t-n)/(n-1);RI=[0 0 0.52 0.89 1.12 1.26 1.36 1.41 1.46 1.49 1.52 1.54 1.56 1.58 1.59]; CR=CI/RI(n); if CR<0.10 disp('此矩陣的一致性可以接受!'); disp('CI=');disp(CI); disp('CR=');disp(CR); else disp('此矩陣的一致性不可以接受!'); end
Saaty吧
很不錯但我想知道判斷 矩陣中的值是怎麼給的多謝
請多人(專家)按照九級打分,取平均值,然後計算。
很不錯但我想知道判斷 矩陣中的值是怎麼給的多謝
由對本項目熟悉的人員(專家)打分,取平均值。
應該是 Saaty, Thomas L 剛看完他的英文版原著
應該是“Saaty”,而不是“Satty”,估計這是個拼寫手誤
你的是對的,我給改過來的,MBA智庫百科是可以自由編輯的,你有更多的資源可以和我們一起編輯分享糾正哦~
好繁瑣啊,選來選去也只是相對較優的策略,就是一句話綜合自己的需求考慮唄。
很不錯但我想知道判斷 矩陣中的值是怎麼給的多謝
一般是專家打分法








提出者是美國運籌學家T.L.Satty,而不是seaty?能否確認一下?