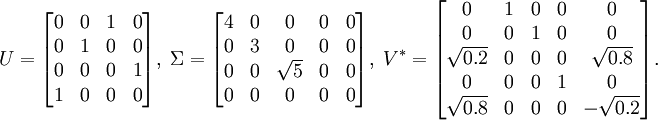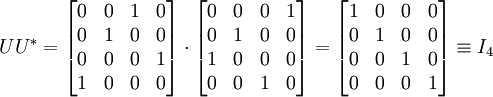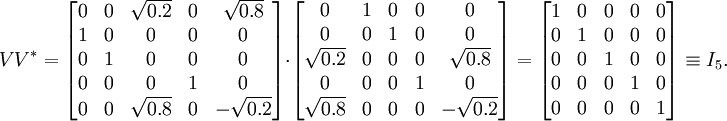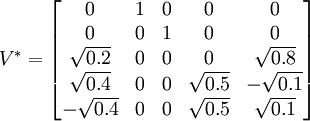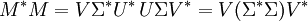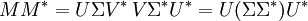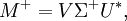奇異值分解
出自 MBA智库百科(https://wiki.mbalib.com/)
奇異值分解(Singular Value Decomposition)
目錄 |
奇異值分解是線性代數中一種重要的矩陣分解，在信號處理、統計學等領域有重要應用。奇異值分解在某些方面與對稱矩陣或Hermitian矩陣基於特征矢量的對角化類似。然而這兩種矩陣分解儘管有其相關性，但還是有明顯的不同。對稱陣特征矢量分解的基礎是譜分析，而奇異值分解則是譜分析理論在任意矩陣上的推廣。
假設M是一個m×n階矩陣，其中的元素全部屬於域K，也就是實數域或複數域。如此則存在一個分解使得
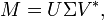
其中U是m×m階酉矩陣；Σ是m×n階實數對角矩陣；而V*，即V的共軛轉置，是n×n階酉矩陣。這樣的分解就稱作M的奇異值分解。Σ對角線上的元素Σi,i即為M的奇異值。
常見的做法是將奇異值由大而小排列。如此Σ便能由M唯一確定了。（雖然U和V仍然不能確定。）
在矩陣M的奇異值分解中
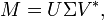
V的列（columns）組成一套對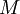
的正交"輸入"或"分析"的基矢量。這些矢量是
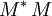的特征矢量。
U的列（columns）組成一套對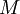的正交"輸出"的基矢量。這些矢量是
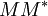的特征矢量。
Σ對角線上的元素是奇異值，可視為是在輸入與輸出間進行的純量的"膨脹控制"。這些是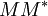及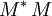的特征值的非零平方根，並與U和V的行矢量相對應。
一個非負實數σ是M的一個奇異值僅當存在Km的單位矢量u和Kn的單位矢量v如下：
Mv = σu and M * u = σv
其中矢量u和v分別為σ的左奇異矢量和右奇異矢量。
對於任意的奇異值分解
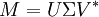
矩陣Σ的對角線上的元素等於M的奇異值. U和V的列分別是奇異值中的左、右奇異矢量。因此，上述定理表明：
一個m×n的矩陣至少有一個最多有p = min(m,n)個不同的奇異值；
總能在Km中找到由M的左奇異矢量組成的一組正交基U，；
總能在Kn找到由M的右奇異矢量組成的一組正交基V，。
如果對於一個奇異值，可以找到兩組線性無關的左（右）奇異矢量，則該奇異值稱為簡並的（或退化的）。
非退化的奇異值在最多相差一個相位因數exp(iφ)（若討論限定在實數域內，則最多相差一個正負號）的意義下具有唯一的左、右奇異矢量。因此，如果M的所有奇異值都是非退化且非零，則除去一個可以同時乘在U,V上的任意的相位因數外，M的奇異值分解唯一。
根據定義，退化的奇異值具有不唯一的奇異矢量。因為，如果u1和u2為奇異值σ的兩個左奇異矢量，則它們的任意歸一化線性組合也是奇異值σ一個左奇異矢量，右奇異矢量也具有類似的性質。因此，如果M具有退化的奇異值，則它的奇異值分解是不唯一的。
觀察一個4×5的矩陣
M矩陣的奇異值分解如下UΣV *
註意矩陣Σ的所有非對角元為0。矩陣U和V * 都是酉矩陣，它們乘上各自的共軛轉置都得到單位矩陣。如下所示。在這個例子中，由於U和V * 都是實矩陣，故它們都是正交矩陣。
由於Σ有一個對角元是零，故這個奇異值分解值不是唯一的。例如，選擇V使得
能得到M的另一個奇異值分解。
奇異值分解能夠用於任意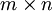
矩陣，而特征分解只能適用於特定類型的方陣，故奇異值分解的適用範圍更廣。不過，這兩個分解之間是有關聯的。給定一個M的奇異值分解，根據上面的論述，兩者的關係式如下：
關係式的右邊描述了關係式左邊的特征值分解。於是：
V的列矢量（右奇異矢量）是M * M的特征矢量。
U的列矢量（左奇異矢量）是MM * 的特征矢量。
Σ的非零對角元（非零奇異值）是M * M或者MM * 的非零特征值的平方根。
特殊情況下，當M是一個正規矩陣（因而必須是方陣）根據譜定理，M可以被一組特征矢量對角化，所以它可以表為：
M = UDU *
其中U為一個酉矩陣，D為一個對角陣。如果M是半正定的，M = UDU * 的分解也是一個奇異值分解。
然而，一般矩陣的特征分解跟奇異值分解不同。特征分解如下：
M = UDU − 1
其中U是不需要是酉的，D也不需要是半正定的。而奇異值分解如下：
M = UΣV *
其中Σ是對角半正定矩陣，U和V是酉矩陣，兩者除了通過矩陣M沒有必然的聯繫。
奇異值分解可以被用來計算矩陣的偽逆。若矩陣M的奇異值分解為M = UΣV * ，那麼M的偽逆為
其中Σ + 是Σ的偽逆，是將Σ主對角線上每個非零元素都求倒數之後再轉置得到的。求偽逆通常可以用來求解最小二乘法問題。
奇異值分解的另一個應用是給出矩陣的行空間與列空間|列空間、零空間和秩 (線性代數)|秩的表示。對角矩陣Σ的非零對角元素的個數對應於矩陣M的秩。與零奇異值對應的右奇異矢量線性生成空間|生成矩陣M的零空間，與非零奇異值對應的左奇異矢量則生成矩陣M的列空間。線上性代數數值計算中奇異值分解一般用於確定矩陣的有效秩，這是因為，由於舍入誤差，秩虧矩陣的零奇異值可能會表現為很接近零的非零值。
