複合套期保值

出自 MBA智库百科(https://wiki.mbalib.com/)

　　採用多種套期保值(如採用多種期貨合約或期權)的套期保值為複合套期保值。

　　人們通常把價格風險劃分為系統風險和非系統風險兩類。系統風險是指對市場上所有資產價格都有影響的風險，包括政策影響、巨集觀經濟因素等各種風險。非系統風險是指只對單個資產產生影響的風險。同樣，投資者所構築的投資組合也面臨著系統風險和非系統風險。現假定投資組合中包含n項資產，每項資產在投資組合中所占權重為ω_i,ω_j,第i,j種期貨合約的方差分別為δ_i,δ_j,價格為ρ_i,j,按照Markowitz投資組合理論，該組合的收益方差即價格風險

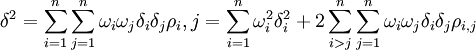
　　由上式可看到，隨著組合中包含的資產數n逐漸擴大，非系統風險逐漸減小，並最終趨近於零.因此，非系統風險可通過組合的充分分散化而消除掉.但是系統風險卻不能分散，隨著n逐漸變大，系統風險將趨於投資組合所包含的任意兩項資產協方差的平均值.

　　對於側重投資證券市場的投資者，其利用股指期貨進行套期保值的目的主要是規避系統風險，其原理可簡單表述為：假定某投資者持有一單位證券組合A，其價格為S，Beta繫數為β，r_s是該組合的收益率；一單位股票指數組合為M，r_M是股票指數組合的收益率.則該投資者持有的證券組合收益就分別包括系統風險βr_m和非系統風險帶來的收益r_u，即

　　r_s = βr_M + r_u

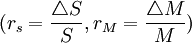　　　　(1)

　　式(1)兩邊同乘以S,可以推出

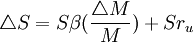
　　假定投資者購買n_f單位股指期貨合約對該組合進行套期保值，則新的組合價值

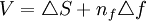　　　　（２）

　　(2)式中，V為新的組合價值，f為股指期貨合約價值，n_f就是套期保值率。

　　為使證明簡單化，假設期貨合約價格變化與股票指數變化一致，則n_f可直接用回歸方法求得，即

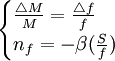　　　　（３）

　　把式（3）代入式（2）中，可得

　　V = Sr_u　　（４）

　　式（４）表明，在運用股指期貨合約進行套期保值後，新的組合已完全剔除了系統風險對價格的影響，組合價值只剩下非系統風險的影響$而非系統風險可通過組合分散化消除，從而鎖定整個組合的風險水平.當然，這隻是最基本的一種套期保值方法，即完全套期保值方法.在實踐中，投資者通常只對證券組合進行部分套期保值，如投資者通常希望能保留系統風險對價格的有利影響，而消除其不利的影響，從而可構築出各種更為高級和複雜的套期保值方法.

　　複合套期保值是一種採用多種期貨合約進行套期保值的方法，而簡單套期保值只採用單種指數期貨合約進行套期保值，簡單套期保值可以看作是複合套期保值的特例.

　　與證券市場一樣，股指期貨市場風險也包括系統風險和非系統風險兩種$當採用簡單套期保值方法時，非系統風險會影響股指期貨合約價格波動，從而降低期貨合約價格與股票指數的相關程度，並最終影響套期保值效果.非系統風險可通過組合分散化消除，而複合套期保值基本原理正是利用了分散化相伴而來的非系統風險減少，從而比簡單套期保值達到更多地減少非系統風險的目的，確保了複合後的套期保值工具與股票指數的相關程度，使覆核後的套期保值更具效率。

　　與有價證券組合不同，複合套期保值並不能完全消除非系統風險，這主要是因為現實的股指期貨市場能夠上市並且同時進行交易的合約品種通常只有幾種，能夠使用的交叉套期保值工具相對不足$但是，這並不影響複合套期保值方法使用上的優越性，因為非系統風險在分散化的初始階段會有顯著下降，從而一個僅包含兩三種不同期貨合約的複合套期保值也能提供顯著的好處。

　　複合套期保值能更大限度地降低非系統風險，具有比簡單套期保值更好的套期保值效果。對此，可用套期保值績效評價辦法來做簡單對比如下：首先可以計算出每一種股指期貨合約的套期保值率n_i，並定義每一單位“調整後的期貨合約”等於n_i份原有的股指期貨合約。比如第i種期貨合約的最優套期保值率為2，則一單位調整後的套期保值工具就由兩單位的第"種期貨構成。這樣，所有經過調整後的股指期貨合約的最優套期保值率就都為1，從而整個複合套期保值的基差方差:

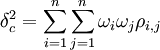
　　假定股指期貨市場有不同到期月份的)A,B和C三種期貨合約，每種合約的套期保值成本相同,此外，假設每一個指數期貨合約套期保值的有效性和基差方差如1表所示。

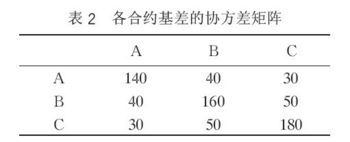
　　如果投資者採用簡單套期保值方法，就會選用合約A作為套期保值工具,假定合約A,B和C基差的協方差矩陣已知，見表2.

　　現在假定投資者在獲知各合約基差的協方差矩陣後，決定採用複合套期保值方法，並且每個合約的權重相同（都為1/3），於是可以計算出複合套期保值後的基差方差

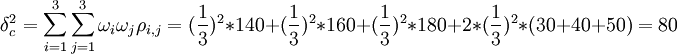
　　則複合套期保值的有效性為

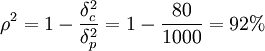
　　因此，在假定各合約的套期保值成本相同的情況下，採用複合套期保值的有效性92%大大高於採用簡單套期保值中有效性最高的83%,當然上述方案只是做了簡化處理後的情形，對於其他情形，仍然可以得出相同的結果，即複合套期保值要比簡單套期保值優越,

　　從本質上說，複合套期保值的風險降低來源於兩個方面：

　　(1)套期保值所固有的風險降低；

　　(2)通過證券組合多樣化將風險降低。

　　因此可以說，複合套期保值是馬柯維茨的證券組合理論在套期保值上的應用。