一元線性回歸預測法
出自 MBA智库百科(https://wiki.mbalib.com/)
一元線性回歸預測模型(Unary Linear Regression Model)
目錄 |
一元線性回歸預測法是分析一個因變數與一個自變數之間的線性關係的預測方法。 常用統計指標:平均數、增減量、平均增減量
確定直線的方法是最小二乘法 最小二乘法的基本思想:最有代表性的直線應該是直線到各點的距離最近。然後用這條直線進行預測。
1、選取一元線性回歸模型的變數 ;
2、繪製計算表和擬合散點圖 ;
3、計算變數間的回歸繫數及其相關的顯著性 ;
4、回歸分析結果的應用 。
1、經濟意義檢驗:就是根據模型中各個參數的經濟含義,分析各參數的值是否與分析對象的經濟含義相符。
2、回歸標準差檢驗
3、擬合優度檢驗
4、回歸繫數的顯著性檢驗
可以分為:點預測和置信區間預測法
1、點預測法:將自變數取值帶入回歸預測模型求出因變數的預測值。
2、置信區間預測法:估計一個範圍,並確定該範圍出現的概率。置信區間的大小的影響的因素:a、因變數估計值;b、回歸標準差;C、概率度t;
一元線性回歸分析預測法模型分析[1]
一元線性回歸分析預測法,是根據自變數x和因變數Y的相關關係,建立x與Y的線性回歸方程進行預測的方法。由於市場現象一般是受多種因素的影響,而並不是僅僅受一個因素的影響。所以應用一元線性回歸分析預測法,必須對影響市場現象的多種因素做全面分析。只有當諸多的影響因素中,確實存在一個對因變數影響作用明顯高於其他因素的變數,才能將它作為自變數,應用一元相關回歸分析市場預測法進行預測。
一元線性回歸分析法的預測模型為:
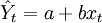 (1)
(1)
式中,xt代表t期自變數的值;
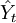 代表t期因變數的值;
代表t期因變數的值;
a、b代表一元線性回歸方程的參數。
a、b參數由下列公式求得(用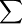 代表
代表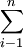 ):
):
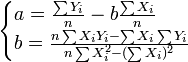
為簡便計算,我們作以下定義:
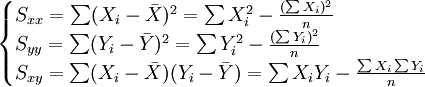 (2)
(2)
式中: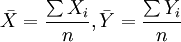
這樣定義a、b後,參數由下列公式求得:
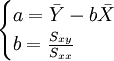 (3)
(3)
將a、b代入一元線性回歸方程Yt = a + bxt,就可以建立預測模型,那麼,只要給定xt值,即可求出預測值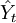 。
。
在回歸分析預測法中,需要對X、Y之間相關程度作出判斷,這就要計算相關係數r,其公式如下:
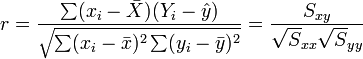
相關係數r的特征有:
①相關係數取值範圍為:-1≤r≤1 。
②r與b符合相同。當r>0,稱正線性相關,Xi上升,Yi呈線性增加。當r<0,稱負線性相關,Xi上升,Yi呈線性減少。
③|r|=0,X與Y無線性相關關係;|r|=1,完全確定的線性相關關係;0<|r|<1,X與Y存在一定的線性相關關係;|r|>0.7,為高度線性相關;0.3<|r|≤0.7,為中度線性相關;|r|≤0.3,為低度線性相關。
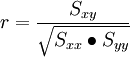 (4)
(4)
- ↑ 朱啟保主編.市場調查與預測.中國科學技術大學出版社,2009.07..








感謝