一元线性回归预测法
出自 MBA智库百科(https://wiki.mbalib.com/)
一元线性回归预测模型(Unary Linear Regression Model)
目录 |
一元线性回归预测法是分析一个因变量与一个自变量之间的线性关系的预测方法。 常用统计指标:平均数、增减量、平均增减量
确定直线的方法是最小二乘法 最小二乘法的基本思想:最有代表性的直线应该是直线到各点的距离最近。然后用这条直线进行预测。
1、选取一元线性回归模型的变量 ;
2、绘制计算表和拟合散点图 ;
3、计算变量间的回归系数及其相关的显著性 ;
4、回归分析结果的应用 。
1、经济意义检验:就是根据模型中各个参数的经济含义,分析各参数的值是否与分析对象的经济含义相符。
2、回归标准差检验
3、拟合优度检验
4、回归系数的显著性检验
可以分为:点预测和置信区间预测法
1、点预测法:将自变量取值带入回归预测模型求出因变量的预测值。
2、置信区间预测法:估计一个范围,并确定该范围出现的概率。置信区间的大小的影响的因素:a、因变量估计值;b、回归标准差;C、概率度t;
一元线性回归分析预测法模型分析[1]
一元线性回归分析预测法,是根据自变量x和因变量Y的相关关系,建立x与Y的线性回归方程进行预测的方法。由于市场现象一般是受多种因素的影响,而并不是仅仅受一个因素的影响。所以应用一元线性回归分析预测法,必须对影响市场现象的多种因素做全面分析。只有当诸多的影响因素中,确实存在一个对因变量影响作用明显高于其他因素的变量,才能将它作为自变量,应用一元相关回归分析市场预测法进行预测。
一元线性回归分析法的预测模型为:
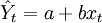 (1)
(1)
式中,xt代表t期自变量的值;
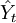 代表t期因变量的值;
代表t期因变量的值;
a、b代表一元线性回归方程的参数。
a、b参数由下列公式求得(用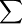 代表
代表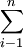 ):
):
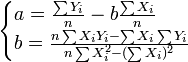
为简便计算,我们作以下定义:
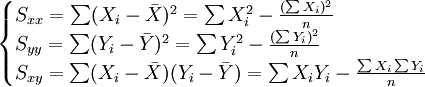 (2)
(2)
式中: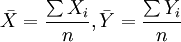
这样定义a、b后,参数由下列公式求得:
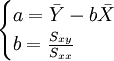 (3)
(3)
将a、b代入一元线性回归方程Yt = a + bxt,就可以建立预测模型,那么,只要给定xt值,即可求出预测值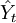 。
。
在回归分析预测法中,需要对X、Y之间相关程度作出判断,这就要计算相关系数r,其公式如下:
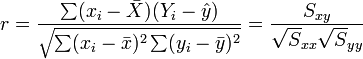
相关系数r的特征有:
①相关系数取值范围为:-1≤r≤1 。
②r与b符合相同。当r>0,称正线性相关,Xi上升,Yi呈线性增加。当r<0,称负线性相关,Xi上升,Yi呈线性减少。
③|r|=0,X与Y无线性相关关系;|r|=1,完全确定的线性相关关系;0<|r|<1,X与Y存在一定的线性相关关系;|r|>0.7,为高度线性相关;0.3<|r|≤0.7,为中度线性相关;|r|≤0.3,为低度线性相关。
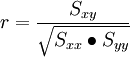 (4)
(4)
- ↑ 朱启保主编.市场调查与预测.中国科学技术大学出版社,2009.07..








感谢