ARIMA模型
出自 MBA智库百科(https://wiki.mbalib.com/)
自回归移动平均模型(Autoregressive Integrated Moving Average Model,简记ARIMA)
目录 |
ARIMA模型全称为自回归移动平均模型(Autoregressive Integrated Moving Average Model,简记ARIMA),是由博克思(Box)和詹金斯(Jenkins)于70年代初提出的一著名时间序列预测方法,所以又称为box-jenkins模型、博克思-詹金斯法。其中ARIMA(p,d,q)称为差分自回归移动平均模型,AR是自回归, p为自回归项; MA为移动平均,q为移动平均项数,d为时间序列成为平稳时所做的差分次数。
ARIMA模型的基本思想是:将预测对象随时间推移而形成的数据序列视为一个随机序列,用一定的数学模型来近似描述这个序列。这个模型一旦被识别后就可以从时间序列的过去值及现在值来预测未来值。现代统计方法、计量经济模型在某种程度上已经能够帮助企业对未来进行预测。
(一)根据时间序列的散点图、自相关函数和偏自相关函数图以ADF单位根检验其方差、趋势及其季节性变化规律,对序列的平稳性进行识别。一般来讲,经济运行的时间序列都不是平稳序列。
(二)对非平稳序列进行平稳化处理。如果数据序列是非平稳的,并存在一定的增长或下降趋势,则需要对数据进行差分处理,如果数据存在异方差,则需对数据进行技术处理,直到处理后的数据的自相关函数值和偏相关函数值无显著地异于零。
(三)根据时间序列模型的识别规则,建立相应的模型。若平稳序列的偏相关函数是截尾的,而自相关函数是拖尾的,可断定序列适合AR模型;若平稳序列的偏相关函数是拖尾的,而自相关函数是截尾的,则可断定序列适合MA模型;若平稳序列的偏相关函数和自相关函数均是拖尾的,则序列适合ARMA模型。
(四)进行参数估计,检验是否具有统计意义。
(五)进行假设检验,诊断残差序列是否为白噪声。
(六)利用已通过检验的模型进行预测分析。
| Glossary of statistical terms | |
|---|---|
| Language | Description |
| English | Box-Jenkins model |
| French | modèle de Box-Jenkins |
| German | Box-Jenkins-Modell |
| Dutch | Box-Jenkins-model |
| Italian | modello Box-Jenkins |
| Spanish | modelo de Box-Jenkins |
| Catalan | model de Box-Jenkins |
| Romanian | modelul Box-Jenkins |
| Finnish | Boxin-Jenkinsin mallit |
| Hungarian | Box-Jenkins-modell |
| Turkish | Box-Jenkins modeli |
| Estonian | Box-Jenkinsi mudel |
| Lithuanian | Box ir Jenkins modelis ; Bokso ir Dženkinso modelis |
| Slovenian | Box-Jenkinsova model |
| Polish | model Boxa-Jenkinsa |
| Russian | Модель Бокса-Дженкинса |
| Ukrainian | модель Бокса - Дженкінса |
| Farsi | modele Box-Jenkins |
| Persian-Farsi | مدل باکس-جنکينز |
| Arabic | نموذج بوكس - جنكز |
| Afrikaans | Box-Jenkins-model |
| Chinese | 博克斯―詹金斯模型 |
2008年。海关税收预算计划8400亿元.比2007年实际完成数增加10.8%,比2007年预算数增加22.1%。为了对2008年江门海关税收总体形势进行把握,笔者尝试利用SAS统计分析软件的时间序列预测模块建立ARIMA模型,对2008年江门海关税收总值进行预测。从预测结果来看,预测模型拟合度较高,预测值也切合实际情况,预测模型具有一定的应用价值。现将预测的方法、原理以及影响税收工作的相关因素分析。
一、ARlMA模型原理
ARIMA模型全称为自回归移动平均模型(Autoregressive Integrated Moving Average Model,简记ARIMA)。是由博克思(Box)fFfl詹金斯(Jenkins)于70年代初提出的一著名时问序列预测方法,所以又称为box--jenkins模型、博克思一詹金斯法。其中ARIMA(p,d.q)称为差分自回归移动平均模型,AR是自回归,P为自回归项;MA为移动平均,q为移动平均项数,d为时间序列成为平稳时所做的差分次数。ARIMA模型可分为3种:(1)自回归模型(简称AR模型);(2)滑动平均模型(简称MA模型);(3)自回归滑动平均混合模型(简称ARIMA模型)。
ARIMA模型的基本思想是:将预测对象随时问推移而形成的数据序列视为—个随机序列.以时间序列的自相关分析为基础.用一定的数学模型来近似描述这个序列。这个模型一旦被识别后就可以从时间序列的过去值及现在值来预测未来值。ARlMA模型在经济预测过程中既考虑了经济现象在时间序列上的依存性,又考虑了随机波动的干扰性,对于经济运行短期趋势的预测准确率较高,是近年应用比较广泛的方法之一。
二、应用ARIMA模型进行预测
每月税收数据.可以看作是随着时间的推移而形成的一个随机时间序列,通过对该时间序列上税款值的随机性、平稳性以及季节性等因素的分析,将这些单月税收值之间所具有的相关性或依存关系用数学模型描述出来,从而达到利用过去及现在的税收值信息来预测未来税收情况的目的。
(一)对序列取对数和作差分处理,形成稳定随机序列
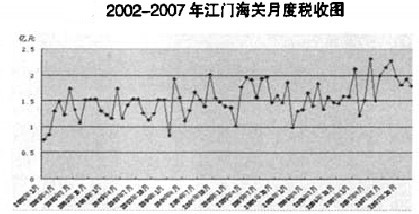
ARIMA模型建模的基本条件是要求待预测的数列满足平稳的条件,即个体值要围绕序列均值上下波动,不能有明显的上升或下降趋势,如果出现上升或下降趋势,需要对原始序列进行差分平稳化处理。
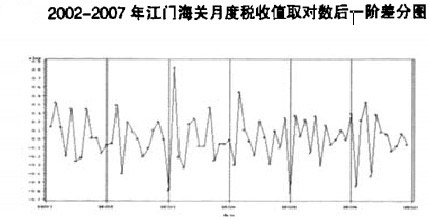
从上图可看出,江门海关自2002年以来的实际入库税收值数列波动性较明显,且呈现出一定的上升趋势,不能直接用ARIMA模型进行建模。取对数可以消除数据波动变大趋势,对数列进行一阶差分,可以消除数据增长趋势性和季节性。从下图可以看出,预测数列取对数并作一阶差分后的图形显示基本消除了长期趋势性的影响,趋于平稳化,满足ARIMA模型建模的基本要求。
(二)模型参数的估计
时间序列预测模块的自相关分析包括对自相关系数和偏相关系数的分析,通过对比分析从而实现对时间序列特性的识别。从计算结果可知,自相关函数1步截尾,偏自相关函数2步截尾,白相关函数通过白噪声检验。根据变换数列的自相关函数和偏自相关函数的特点,并经过反复测试,对ARIMA模型的参数进行估计.三个参数定为d=l,p=2和q=l。
对参数进行检验。从检验结果可知,参数估计全部通过显著性检验.拟合优度统计量表中给出了残差序列的方差(0.063367)和标准误差(0.251729),以及按AIC和SBC标准计算的统计量(9.496798)和(18.54752),这两个值都较小,表明对预测模型拟合得较好。从残差的自相关检验结果数据中.可以得知残差通过白噪声显著性检验。预测模型最终形式为:(14-0.98284B)(1+0.56103B-2)Z=(1-0.34111B)(1+B)u其中,Z=logX。B为后移算子,u为随机干扰项(三)应用模型预测。
利用上面确定的模型进行预测。预测模型x.-J 2007年税收的拟合值是21.75亿元,跟实际税收值22.58亿元比较,误差为3.7%,表明预测模型拟合度较高,预测模型具有一定的应用fir值。把预测模型向前推12个月进行预测,得到2008年各月税收数据,全年累计税收预计均值为23.5亿元,实际税收值会围绕此值上下波动。需要说明的是,由于利用模型向前预测1一12月的数据,预测时间越长,难度越大,预测精度也下降,若到年中再次预测时,预测精度将会进一步提高。
这个税收预测值是基于当前海关监管水平、税收征管水平不变或提高的基础上,挖掘税收样本数据自身涵盖的信息.利用数理统计分析方法,建立预测模型得出的理论预测值,一旦实际外部环境和条件发生变化,例如国家实施宏观调控、人民币升值过快、汇率大幅变动、对外经济政策的变化等,将对税收预测结果生一定的影响。
三、其他可能对2008年税收工作产生影响的主要因素
(一)个别商品税收变化影响巨大
2007年占关区税收总值80%前20位大类税源商品,与2006年占关区税收总值80%前20位大类税源商品相比,新增了大豆、印刷和装订机械及零件、棉纱线,少了空气调节器、初级形状的聚丙烯和初级形状的聚乙烯.新增的三项商品税收总值为3.1亿元。占关区税收总值13.8%,其中,大豆2007年税款高达2.6亿元,2006年仅为15万元,影响巨大。另外,煤和钢材的税收值大幅增长。液化石油气、纺织品(包括服装和纺织纱线)、纸及纸板(未切成形的)税收下降幅度较大。
主要税源商品的不稳定,为关区税收工作增加了难度。
(二)本地企业异地纳税仍保持较大规模
据统计,2007年江门关区企业在异地进口异地报关应税货值85.2亿元人民币,比2006年增长13.6%,应征税收为9.2亿元,较2006年增长7.4%.占江门区同期应征税收总额的四成多。
从口岸分布来看,大部分本地企业异地纳税进口行为分布在广州口岸。在广州口岸纳税4.7亿元,下降占异地纳税总值的51.1%。另外。在黄埔口岸纳税1.7亿元,下降4.8%;在拱北口岸纳税1.3亿元,增加3倍从商品来看,异地纳税进口的商品主要是废塑料、废五金、木浆、冰乙酸、正丁醇、脂肪醇、冻猪杂碎、IEl挖掘机、初级形状聚乙烯等商品,税款均超过千万元,部分商品曾经在本关区口岸大量进口。废塑料进口3亿元,下降10.9%;废五金进口1.2亿元,增长87.6%;木浆进口7783万元,增长17.2%;冰乙酸进口6593万元,下降19.4%;正丁醇进口3498万元,增长3.5倍;脂肪醇进口3366万元。32.3%;冻猪杂碎进口3313万元,增长2.3倍;旧挖掘机进口3101万元,下降1.7%;初级形状聚乙烯进口2539万元,下降54%。其中正丁醇、冻猪杂碎和废五金进口增长迅猛。
(三)主要纳税大户变化较大
2007年占关区税收总值60%前20位纳税企业,与2006年占关区税收总值60%前20位纳税企业相比,有12家企业新上榜,更新率为60%。新增的2家纳税企业嘉吉投资(中国)有限公司和北京华特安科经贸有限公司共纳税3.4亿元,占关区税收总值的15%。影响巨大。而海洋石油阳江实业有限公司的纳税额从2006年的1.4亿元下降到2783万元,该企业的税款下fl手x,l 2007年关区税收工作带来了较大的影响。主要纳税大户的不稳定,加大了2008年关区税收工作的不确定性。
(四)加工贸易内销补税和出口征税的影响
2007年,江门关区一般贸易应征税收为21.5亿元,增长26.5%;加工贸易内销补税(不含后续补税)为7909万元,增长11.3%;后续补税为594万元,增长49.3%。2007年江门关区出口商品征税160万元,增长1.8倍。江门关区的税收以一般贸易进口征税为主,但由于加工贸易进出口值占关区进出口总值的比重超过一半.因而加强加工贸易内销征税工作,充分挖掘加贸内销补税潜力,可以为关区税收总量增长提供支持。虽然当前出口征税占关区税收总值的比重非常少,但由于国家不断调整外贸政策,2008年出口需要征收关税商品涉及300多个税号,而且相当多的商品出口关税率高达15—20%,预计江门关区出口关税将会保持大幅增长态势,为关区税收总量增长提供补充。
综合来看,只要大类税源商品如己内酰胺、大豆、煤、钢材和废纸等保持2007年的进口规模,其他税源商品进口没有大幅下降,2008年的税收总额就能够保持甚至超过2007年的税收水平,如果液化石油气、纺织品和纸及纸板恢复2006年的进口水平,同时将本关区企业从异地报关引导回本关区报关,今年税收总额将比2007年小幅增长。结合应用前面的时间序列模型的预测结果,综合多方面因素,预计全年累计税收均值为23.5亿元。
案例二:基于ARIMA模型的备件消耗预测方法[1]
一、引言
随着技术的进步和军事的变革,快速响应战场需求是装备战斗力的重要指标之一。要快速响应战场需求就要有强有力的后勤保障和支持,部队需要保证有一定数量备件。而实际中却常常由于没有足够的备件导致装备不能快速形成战斗力。由于造成备件短缺的重要原因是使用的备件需求预测方法和模型不够精确[2],故尝试用差分自回归滑动平均模型,即ARIMA(p,d,q)模型,对备件消耗进行预测。
1备件消耗预测的ARIMA(p,d,q)模型求和自回归滑动平均模型(AutoregressiveIntegrated Moving Average Model,简称ARIMA),由Box和Jenkins于70年代初提出的时间序列预测方法,又称为B-J模型、博克思-詹金斯法[3]。其中ARIMA(p,d,q)称为差分自回归滑动平均模型,AR是自回归,MA为滑动平均,p、q分别为对应的阶数,d为时间序列成为平稳时所做的差分次数。
1.基本思路
首先需要明确建立模型的前提是在预测的这段时间内,影响该类备件消耗量的主要因素不发生大变故。在此前提下,将备件消耗的历史统计数据视为一个时间序列,即为一组依赖于时间t的随机变量序列。这些变量间有依存性和相关性,并表现出一定的规律性,如能根据这些消耗数据建立尽可能合理的统计模型,就能用这些模型来解释数据的规律性,就可利用已得到的备件消耗数据来预测未来消耗数据,也就能得出备件需求做好的备件供应。
2.模型描述
备件消耗预测ARIMA(p,d,q)模型实质是先对非平稳的备件消耗历史数据Yt进行d(d=0,1,dots,n)次差分处理得到新的平稳的数据序列Xt,将Xt拟合ARMA(p,q)模型,然后再将原d次差分还原,便可以得到Y_t的预测数据。其中,ARMA(p,q)的一般表达式为:
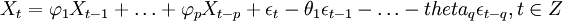 (1)
(1)
式中,前半部分为自回归部分,非负整数p为自回归阶数,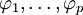 为自回归系数,后半部分为滑动平均部分,非负整数q为滑动平均阶数,
为自回归系数,后半部分为滑动平均部分,非负整数q为滑动平均阶数,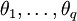 为滑动平均系数;Xt为备件消耗数据相关序列,εt为WN(0,σ2)。
为滑动平均系数;Xt为备件消耗数据相关序列,εt为WN(0,σ2)。
当q=0时,该模型成为AR(p)模型: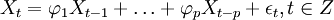 (2)
(2)
当p=0时,该模型成为MA(q)模型: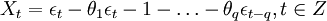 (3)
(3)
3.备件消耗预测建模流程
通过建立ARIMA(p,d,q)模型进行备件消耗预测的基本流程,如下图。
(1)获取数据并进行预处理.收集装备使用阶段某备件消耗的数据序列,记为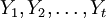 。利用游程检验法[4]来判断该序列是否为平稳序列,如为非平稳序列,用差分的方法,即:
。利用游程检验法[4]来判断该序列是否为平稳序列,如为非平稳序列,用差分的方法,即: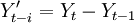 ,对序列进行平稳化预处理,每次差分后数据进行游程检验,直到差分所得数据可以通过平稳性检验,记为d次差分,得到新的平稳序列
,对序列进行平稳化预处理,每次差分后数据进行游程检验,直到差分所得数据可以通过平稳性检验,记为d次差分,得到新的平稳序列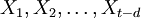 。
。
取前N组(或全部)数据作为观测数据,进行零均值化处理,即: ,得到一组预处理后的新序列
,得到一组预处理后的新序列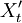 。
。
(2)ARMA模型的识别
通过计算预处理后的序列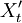 的自相关函数(ACF)
的自相关函数(ACF)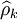 和偏自相关函数(PACF)
和偏自相关函数(PACF)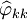 来进行模型识别。具体的计算公式为:
来进行模型识别。具体的计算公式为:
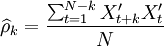 (4)
(4)
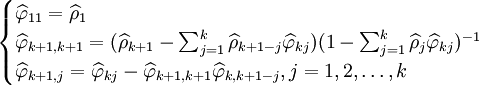 。
。
根据上述计算结果,并依据表1的模型识别原则,可以确定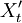 符合的模型。
符合的模型。
ARMA(p,q)模型识别原则
| 模型 | AR(p) | MA(q) | ARMA(p.q) |
| 自相关函数 | 拖尾,指数衰减或振荡 | 有限长度,截尾(q步) | 拖尾,指数衰减或振荡 |
| 偏自相关函数 | 有限长度,截尾(p步) | 拖尾,指数衰减或振荡 | 拖尾,指数衰减或振荡 |
(3)参数估计和模型定阶
参数估计和模型定阶是建立备件消耗预测模型的重要内容,二者相互影响。
在上述模型识别的基础上,利用样本矩估计法、最小二乘估计法或极大似然估计法等对ARMA(p,q)的未知参数,即自回归系数、滑动平均系数以及白噪声方差进行估计,得出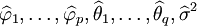 。
。
利用AIC、BIC准则进行模型定阶。具体步骤[5]。
(4)模型检验
首先要检验所建立模型是否能满足平稳性和可逆性,既要求下式(6)、式(7)根在单位圆外,具体公式如下:
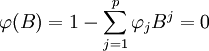 (6)
(6)
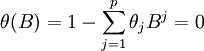 (7)
(7)
再进一步判断上述模型的残差序列是否为白噪声,如果不是,则需要重新进行模型识别,如果是,则通过检验,得出软件可靠性预测模型:
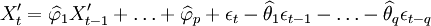 (8)
(8)
(5)备件消耗量预测
根据上述预测模型,依据一步预测的方法对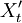 进行预测,并考虑前面所进行的d次差分,还原为备件消耗数据Yt的预测结果,根据该预测结果来进行备件的配置。
进行预测,并考虑前面所进行的d次差分,还原为备件消耗数据Yt的预测结果,根据该预测结果来进行备件的配置。
二、案例应用
1.原始数据及预处理
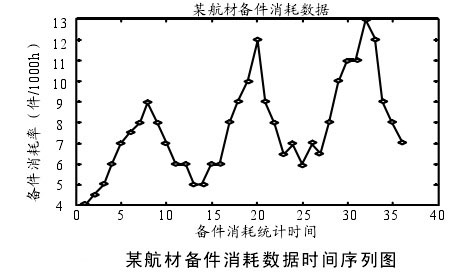
以航空兵场站某种航材备件3年的消耗率(件/1000h)[6]来进行分析和预测。取前30组数据建立模型,并用后面的几组数据对模型进行预测验证。
3年的原始数据的时间序列如下图,是有关备件消耗统计时间(2001年1月到2003年12月)-备件消耗率(件/1000h)的某航材备件消耗数据。
从上图中可以看出,数据有明显递增的趋势,为非平稳序列。尝试进行一次差分对数据进行平稳化处理,结果表明仍未平稳,然后再做一次差分,再对进行2次差分后的数据进行游程检验[4],可以通过检验,故接受数据具有平稳性的原假设。可得出d等于2,并将数据进行零均值化,下面进一步确定ARMA(p,q)模型。
2.建立模型并进行参数估计
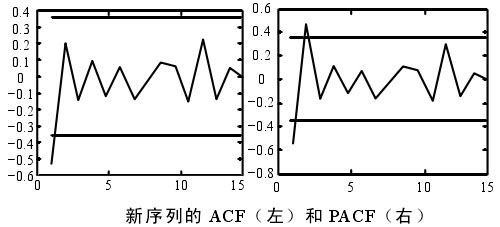
计算零均值化后序列的自相关函数(ACF)和偏自相关函数(PACF),结果如下图。其中,上下两条线为置信区间(±1.96/ )。由图可以看出0≤p≤3,0≤q≤2。尝试建立ARMA(p,q)模型。
)。由图可以看出0≤p≤3,0≤q≤2。尝试建立ARMA(p,q)模型。
对p、q可能的组合进行参数估计,并利用AIC准则进行定阶,并对估计出的参数进行平稳性和可逆性检验,结果表明都在单位圆外,可以初步确定满足要求的最佳模型为ARMA(3,1)模型,即:
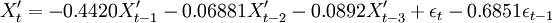 (9)
(9)
式(9)中{εt}为WN(0,1.0943)。
3.白噪声检验
对已经通过平稳性和可逆性检验的模型(9)进行白噪声检验(4≤m≤6),检验结果如图4。
由上图中检验结果可看出,对应于上面m的值,都有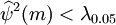 (m),可通过白噪声检验,模型合理。
(m),可通过白噪声检验,模型合理。
4.预测及结果分析
根据模型(9),用一步预测的方法对后4组数据进行预测,并与移动平均法进行对比,如表2。对预测结果进行多角度评价,具体选用的指标包括:平均绝对误差:
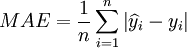 (10)
(10)
平均相对误差:
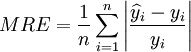 (11)
(11)
预测均方差:
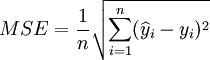 (12)
(12)
其中,y_i为备件消耗序列的实际数据,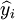 为模型预测数据。
为模型预测数据。
预测结果对比
| 时间 | 真实值 | 移动平均法[5] | ARIMA模型 | ||||||
| 预测值 | MAE | MRE | MSE | 预测值 | MAE | MRE | MSE | ||
| 2003.09 | 12 | 7.2447 | 2.0621 | 21.83% | 1.3524 | 13.4777 | 0.6922 | 6.93% | 0.4298 |
| 2003.10 | 9 | 8.7642 | 9.8088 | ||||||
| 2003.11 | 8 | 8.8250 | 7.7322 | ||||||
| 2003.12 | 7 | 9.4324 | 6.7857 | ||||||
注释:[5]是[7]
由上表预测结果及各项评价指标的对比可知,ARIMA模型预测结果明显优于移动平均法,从平均相对误差上来看,ARIMA模型为6.93%,比移动平均法提高了将近15%,且预测的均方差也较小,仅0.4298。由此可见:该模型能较准确地预测出备件消耗的变化趋势,可为备件消耗量的预测提供依据。
另由于ARIMA模型建立在历史数据的基础上,故搜集的历史数据越多,模型越准确。
该建模方法能综合反映装备使用的实际情况,具有很好的模型适应性。模型具有较高的预测准确度,且有较成熟的软件支持(SPSS、Matlab等),易于推广,可进行备件消耗预测,确定备件需求。
- ↑ 贾治宇,康锐.基于ARIMA模型的备件消耗预测方法[J].兵工自动化,2009,28(6)
- ↑ Hua-kai Chiou,Gwo-Hshiung.Grey Prediction Model Forthe Planning Material of Equipment Spare parts in Navy ofTaiwan[C].Proceedings of World Automation Congress,2004(17):315-320
- ↑ George E.P.Box,Gwilym M.Jenkins.时间序列分析-预测与控制[M].北京:中国统计出版社,1997:101-149
- ↑ 4.0 4.1 张树京,齐立心.时间序列分析简明教程[M].北京:北方交通大学出版社,2003:24-59
- ↑ 王炜炘,杜金观,伍尤桂,等.应用时间序列分析[M].桂林:广西师范大学出版社,1999:102-183
- ↑ 左召军,钟新辉.航材消耗的时间序列分析[J].长沙:航空职业技术学院学报,2004,4(3):29-32
- ↑ Craig C,Sherbrooke.Optimal Inventory Modeling of Systems:Multi-Echelon Techniques[M].Boston:Kluwer Academic Pub,2004
本条目由以下用户参与贡献
蔓草寒烟,苦行者,Vulture,Angle Roh,funwmy,Zfj3000,Cabbage,Dan,Guaigui,Fghghg,Yixi,咪小鸭,Breakinen,连晓雾,y桑,nonameh.评论(共16条)
案例预测精度不高 另外对于季节性arima模型也无介绍,acf、pacf也无图可参考,可以改进 当然,有个参考已经是很好的了,谢谢编辑人员!
博主,你d=2,二阶差分,应该是二阶导,你怎么模型公式写的是一阶导’
没有错啊,它先做一次差分,再进行2次差分后,对数据进行游程检验检验得出,d=2,然后才用数据进行零均值化的求导。










太不专业了,怎么连个数学公式都没有明确写出来。文字表述再多也不行啊。