标准差
出自 MBA智库百科(https://wiki.mbalib.com/)
标准差 (Standard Deviation),也称均方差(Mean square error)
目录 |
标准差是一种表示分散程度的统计观念。标准差已广泛运用在股票以及共同基金投资风险的衡量上,主要是根据基金净值于一段时间内波动的情况计算而来的。一般而言,标准差愈大,表示净值的涨跌较剧烈,风险程度也较大。实务的运作上,可进一步运用单位风险报酬率的概念,同时将报酬率的风险因素考虑在内。所谓单位风险报酬率是指衡量投资人每承担 一单位的风险,所能得到的报酬,以夏普指数最常为投资人运用。
标准差是一组数值自平均值分散开来的程度的一种测量观念。一个较大的标准差,代表大部分的数值和其平均值之间差异较大;一个较小的标准差,代表这些数值较接近平均值。
例如,两组数的集合 {0, 5, 9, 14} 和 {5, 6, 8, 9} 其平均值都是 7 ,但第二个集合具有较小的标准差。
标准差可以当作不确定性的一种测量。例如在物理科学中,做重复性测量时,测量数值集合的标准差代表这些测量的精确度。当要决定测量值是否符合预测值,测量值的标准差占有决定性重要角色:如果测量平均值与预测值相差太远(同时与标准差数值做比较),则认为测量值与预测值互相矛盾。这很容易理解,因为值都落在一定数值范围之外,可以合理推论预测值是否正确。
1.实数的标准差: 假设有一组数值 x1, ..., xN (皆为实数),其平均值为:
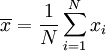
此组数值的标准差为:
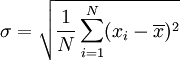
一个较快求解的方式为:
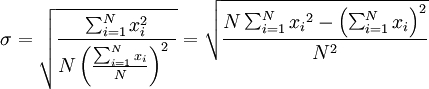 从这组数值当中取出一样本数值组合 x1,...,xn ,常定义其样本标准差:
从这组数值当中取出一样本数值组合 x1,...,xn ,常定义其样本标准差:
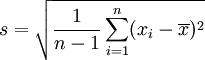 注:在统计学中样本的均差多是除以自由度(n-1),它是意思是样本能自由选择的程度。当选到只剩一个时,它不可能再有自由了,所以自由度是n-1。
注:在统计学中样本的均差多是除以自由度(n-1),它是意思是样本能自由选择的程度。当选到只剩一个时,它不可能再有自由了,所以自由度是n-1。
2.随机变量的标准差 一随机变量X 的标准差定义为:
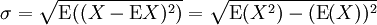
须注意并非所有随机变量都具有标准差,因为有些随机变量不存在期望值。
标准差的特性[1]
注:这些特性同时适用于有偏和无偏公式。
1.如果在一个分布中每个分数都加上(或减去)一个常数,则标准差不变。为了演示均数的这个特性,以一场考试为例。这场考试的平均分为70分。教授决定给每个学生加10分,这使得均数从70增加到80。对于原始考试分数,标准差是15分,在给每个学生增加了10分后标准差仍然是15分。由于均数随分数而移动,而分数与分数之问的相对位置是保持不变的,只是移动了整体分布的位置而已(通过加上或减去一个常数),因此并不改变它的形态(看图1)。一般来说,这用简单代数式来表示也是成立的。每个分数加了一个常数后,分数集的标准差是: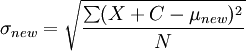
根据均数的特性,μnew = μold + C。因此,![\sigma_{new} = \sqrt{\frac{\sum[(X+C)-(\mu_{old}+C)]^2}{N}}](/w/images/math/7/a/0/7a0358bd83aa3e98c60521b32ae7eb88.png)
对其中各项重排后,得到:
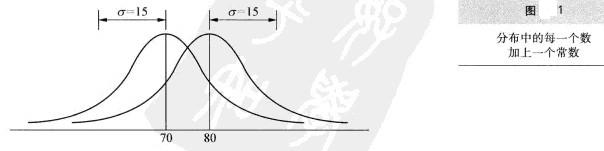
2.如果每一个分数都乘上(或除以)一个常数,则标准差也将乘上(或除以)那个常数。
3.从均数计算的标准差比分布中根据任何其他点计算的标准差都要小。
这里示范如何计算一组数的标准差。例如一群孩童年龄的数值为 { 5, 6, 8, 9 } :
第一步,计算平均值
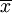
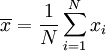
n = 4 (因为集合里有 4 个数),分别设为: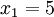 ,
,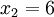 ,
,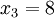 ,
,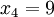
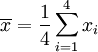 用 4 取代 N
用 4 取代 N
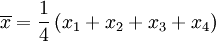
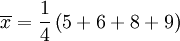
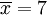 此为平均值。
此为平均值。
第二步,计算标准差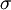
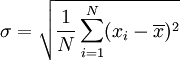
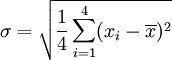 用 4 取代 N
用 4 取代 N
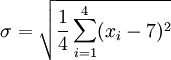 用 7 取代
用 7 取代 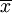
![\sigma = \sqrt{\frac{1}{4} \left [ (x_1 - 7)^2 + (x_2 - 7)^2 + (x_3 - 7)^2 + (x_4 - 7)^2 \right ] }](/w/images/math/1/b/3/1b3ee6d89f69664070242d56103f30b0.png)
![\sigma = \sqrt{\frac{1}{4} \left [ (5 - 7)^2 + (6 - 7)^2 + (8 - 7)^2 + (9 - 7)^2 \right ] }](/w/images/math/6/2/c/62c241b9f368cfa8d1d37b0a53950a55.png)
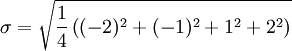
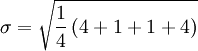
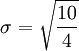
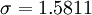
一组数据的平均值及标准差常常同时做为参考的依据。在直觉上,如果数值的中心以平均值来考虑,则标准差为统计分布之一"自然"的测量。较确切的叙述为:假设 x1, ..., xn 为实数,定义其公式
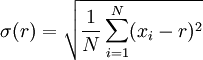
使用微积分,不难算出 σ(r) 在下面情况下具有唯一最小值:
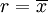
标准差(Standard Deviation)各数据偏离平均数的距离(离均差)的平均数,它是离差平方和平均后的方根。用σ表示。因此,标准差也是一种平均数。标准差是方差的算术平方根。 标准差能反映一个数据集的离散程度。平均数相同的,标准差未必相同。
例如,A、B两组各有6位学生参加同一次语文测验,A组的分数为95、85、75、65、55、45,B组的分数为73、72、71、69、68、67。这两组的平均数都是70,但A组的总体标准差为17.08分,B组的总体标准差为2.16分,说明A组学生之间的差距要比B组学生之间的差距大得多。
标准差在投资决策中的应用[2]
投资是企业生产经营和发展壮大的必要手段。投资者作出投资决策时,不仅要考虑预期回报,还必须分析比较投资风险。
由于投资风险的客观存在性及其对投资收益的不利性,投资者在进行投资决策时必须而且也应该对投资风险进行分析,尽可能地测定和量化风险的大小。
1、用标准差衡量风险大小。此时的标准差计算公式如下:
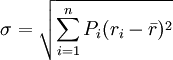
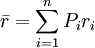
其中σ为标准差,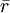 为期望投资收益率,Pi为一系列可能性事件发生的概率,ri为可能性事件发生时的投资收益。标准差值越小,说明投资风险越小。
为期望投资收益率,Pi为一系列可能性事件发生的概率,ri为可能性事件发生时的投资收益。标准差值越小,说明投资风险越小。
假设投资者要在A、B两个项目中选择一个或两个项目进行投资。估计第二年每个项目的收益率可能有四个结果,每个结果都有一个确定的概率与之对应。如下表所示,表中r为收益率,p为收益率实现的可能性。
表1 A、B两项目的收益率分布
A项目 B项目 r p r p 1 0.2 0.25 1.0 0.05 2 0.14 0.25 0.6 0.2 3 0.20 0.25 0.1 0.7 4 0.04 0.25 -1.0 0.05
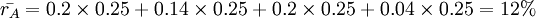
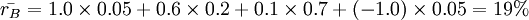
计算结果表明,A项目的期望收益率小于B项目。但从收益率的分布看,A项目的收益率在4%~20%之间波动,变动范围小;而B项目收益率从-100%到+100%,变动范围大。收益率的变动大小反映了风险的大小,收益率变动大,风险就大。根据公式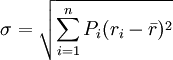 计算得:σA = 5.83%,σB = 37.80%。这是不是说明B项目的风险更大呢?从数学角度看,B项目标准差大可能来源于B项目的各种可能收益都比较大。
计算得:σA = 5.83%,σB = 37.80%。这是不是说明B项目的风险更大呢?从数学角度看,B项目标准差大可能来源于B项目的各种可能收益都比较大。
2、标准差的局限性。当不同项目的期望回报率相同时,用标准差衡量风险程度是合适的,否则就不能再用标准差而必须用一个相对的风险指标。取标准差与期望值的比率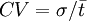 ;,称为变异系数或标准离差,该值越大反映项目的风险越大。
;,称为变异系数或标准离差,该值越大反映项目的风险越大。
可以计算项目A的变异系数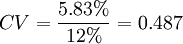 ,项目B的变异系数
,项目B的变异系数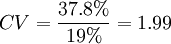 。这个时候就可以说B项目风险更大。
。这个时候就可以说B项目风险更大。
标准差在股市分析中的应用[2]
股票价格的波动是股票市场风险的表现,因此股票市场风险分析就是对股票市场价格波动进行分析。波动性代表了未来价格取值的不确定性,这种不确定性一般用方差或标准差来刻画(Markowitz,1952)。下表是中国和美国部分时段的股票统计指标,其中中国证券市场的数据由“钱龙”软件下载,美国证券市场的数据取自ECI的“world stock Excllarlge Data Disk”。
表2股票统计指标
年份 业绩表现 波动率 上证综指 标准普尔指数 上证综指 标准普尔指数 1996 110.93 16.46 0.2376 O.0573 1997 -0.13 31.01 O.1188 O.0836 1998 8.94 26.67 O.0565 O.0676 1999 17.24 19.53 O.1512 0.0433 2000 43.86 -10.14 0.097 0.0421 2001 -15.34 -13.04 O.0902 O.0732 2002 -20.82 -23.37 O.0582 O.1091
通过计算可以得到:
上证综指业绩期望值≈(110.93-0.13+8.94+17.24+43.86-15.34-20.82)/7=20.67
上证波动率期望值≈0.1156
标准普尔业绩期望值≈6.7214
标准普尔波动率期望值≈0.0680
而标准差的计算公式则根据公式(2)计算:
上证综指的业绩标准差
![=\{ \frac{1}{6}[(110.93-20.67)^2+(0.13-20.67)^2+(8.94-20.67)^2+(17.24-20.67)^2+(43.86-20.67)^2+(-15.34-20.67)^2+(-20.82-20.67)^2]\}^{\frac{1}{2}}\approx 45.2457](/w/images/math/6/e/7/6e79498ee426a487a2b4ad22addf2c30.png)
上证波动率标准差≈0.0632
标准普尔指数业绩标准差≈21.71
标准普尔波动率标准差≈0.02365
因为标准差是绝对值,不能通过标准差对中美直接进行对比,而变异系数可以直接比较。计算可得:
上证业绩变异系数≈45.2457/20.67≈2.1889
上证波动率变异系数≈0.0632/0.1156≈0.5467
标准普尔业绩变异系数≈21.71/6.7214≈3.2299
标准普尔波动率变异系数≈0.02365/0.0680≈0.3478
通过比较可以看出上证波动率变异系数要大于标准普尔波动率变异系数,说明长期来讲中国股市稳定性相对较差,还是一个不太成熟的股票市场。
标准差在确定企业最优资本结构中的应用[2]
资本结构指的是企业各种资金来源的比例关系,是企业筹资活动的结果。最优资本结构是指能使企业资本成本最低且企业价值最大的资本结构;产权比率,即借入资本与自有资本的构成比例,是反映企业资本结构的重要变量。企业的资产由债务性资金和权益性资金组成,但其风险等级和收益率各不相同。根据投资组合理论,投资的多样化可以分散掉一定的风险,因此资金提供者需要决定投资于债务性资金和权益性资金的比例。以便在权衡风险和收益的情况下保证其利益的最大化。
理论探索而外部资金提供者利益的最大化也就是企业价值的最大化,这一投资比例对于企业融资而言也就是企业的最优资本结构比例。
假定某企业的资金通过发行债券和股票两种方式获得,并且都属于风险性资产。σ其中债券的收益率为rD,风险通过标准差σD来衡量;股票的收益率为rE,风险为σE;股票和债券的相关系数为pDE,协方差为COV(rD,rE);债券所占的比重为wD,股票所占比重为WE(WD + WE = 1)。根据投资组合理论,企业外部投资者对该企业投资所获的期望收益率为E(rp) = WDE(rD) + wEE(rE),方差为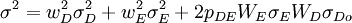
1、企业债务性资金和权益性资金完全正相关,即相关系数pDE为1。企业外部投资者获得的期望收益率为E(rp) = wDE(rD) + wEE(rE),风险标准差为σ = wDσD + wEσE,也就是组合的标准差等于各个部分标准差的加权平均值,通过投资组合不可能分散掉投资风险。根据投资组合理论,投资组合的不同比例对于投资者而言是无差异的。
2、企业债务性资金和权益性资金完全负相关,即其相关系数为-1。投资者获得的报酬率的期望值及其方差分别为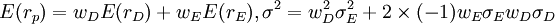 。
。
根据投资组合理论,只有当投资比例大于σE / (σD + σE)时其投资组合才是有效的。对于企业筹资而言,也即企业的权益性资金的比例大干σE / (σD + σE),企业的筹资比例才是有效的,而且当组合比例为σE / (σD + σE)时,企业的筹资组合风险为零。
3、企业债务性资金和权益性资金的相关系数大于-1小于1。理论上,一个企业的两种筹资方式之间的相关程度较高,一方面两种筹资方式都承担系统风险,另一方面它们也承担相同的公司风险。因此从实践来看,企业的不同筹资方式间的相关程度不可能是完全的正相关和负相关。对于一个企业而言,债务性资金对企业有固定的要求权,权益性资金对企业只有剩余要求权,因此债务性资金的波动不可能像权益性资金的波动那么大。同时企业的风险会同时影响企业的债务性资金和权益性资金,因此企业的债务性资金和权益性资金的相关系数不可能为负数。企业不同的筹资方式间的相关系数一般在0-1之间。
那么究竟在什么比例下企业的价值才会达到最大呢?根据投资组合理论,当E(r1) > E(r2),且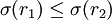 时,才能出现r1,优于r2。
可见,决定企业资本结构的直接因素主要是不同筹资方式的收益率和风险以及它们之间的相关系数。
时,才能出现r1,优于r2。
可见,决定企业资本结构的直接因素主要是不同筹资方式的收益率和风险以及它们之间的相关系数。
本条目由以下用户参与贡献
Angle Roh,苦行者,Vulture,Dan,Cabbage,Zfj3000,Melisa81,鲈鱼,Fd60,Alan Chiu,Tears~,泡芙小姐,jeremy,alen kiu,连晓雾,青青,Lin,潘晓春,M id 7127ae6ed3d66dd3cf8058b1c815a109.评论(共103条)
very clear, and very good. just one thing dont realy understand. The last part, 一组数据的平均值及标准差常常同时做为参考的依据。在直觉上,如果数值的中心以平均值来考虑,则标准差为统计分布之一"自然"的测量。较确切的叙述为:假设 x1, ..., xn 为实数,定义其公式
使用微积分,不难算出 σ(r) 在下面情况下具有唯一最小值:
what does that mean? and whats the relations with standard deviation?
OK! 但一些细节可能有误: 因为标准差是绝对值,不能通过标准差对中美直接进行对比,而变异系数可以直接比较。计算可得:
上证业绩变异系数≈45.2457/20.67≈2.1889
上证波动率变异系数≈0.0632/0.1156≈0.5467
标准普尔业绩变异系数≈21.71/6.7214-3.2299
标准普尔波动率变异系数≈0.02365/0.0680≈0.3478
变异系数或标准离差,该值越大反映项目的风险越大??????? A项目 B项目 r p r p 1 0.9 0.3 0.2 0.3 2 0.6 0.4 0.15 0.4 3 0.3 0.3 0.1 0.3 Average r(A)=60% Average r(B)=15% σ(A)=23% , σ(B)=3.87% CV(A)=23%/60%=38.33% CV(B)=3.87%/15%=25.8% 这种情况A项目跟B项目哪个风险高?
嗯,虽然很好,但是,我真的晕了...似乎初中学的没这么复杂吧...
哎!今天有雨!呵呵!
两个问题比较突出: 1,在“标准差在股市分析中的应用”中,数据计算有错误,而且在套用公式时,7项数据,何以用1/6? 2,作者对何时用公式2,何时用公司3的选择,没有给出具体而明确的说明!
有附上参考文献,您可以对比一下。
MBA智库百科是可以自由参与编辑和修改的百科,如有发现错误和不足,期待您参与修改编辑哦!
标准差的应用分析,计算σB怎么不等于37.80%?
文中的σB是等于37.8%的
这公式看是看懂了,非常清晰,但是我不明白这公式有什么用,可以运用在实际工作中做什么
当然,质量分析,风险投资,我现在觉得是很有用的
OK! 但一些细节可能有误: 因为标准差是绝对值,不能通过标准差对中美直接进行对比,而变异系数可以直接比较。计算可得:
上证业绩变异系数≈45.2457/20.67≈2.1889
上证波动率变异系数≈0.0632/0.1156≈0.5467
标准普尔业绩变异系数≈21.71/6.7214-3.2299
标准普尔波动率变异系数≈0.02365/0.0680≈0.3478
楼主在最后有补充的。。
开头英文注释有错误, Standard Deviation是均方差,标准差 mean squared error 则是均方误差 均方误差是各数据偏离真实值的距离平方和的平均数
变异系数或标准离差,该值越大反映项目的风险越大??????? A项目 B项目 r p r p 1 0.9 0.3 0.2 0.3 2 0.6 0.4 0.15 0.4 3 0.3 0.3 0.1 0.3 Average r(A)=60% Average r(B)=15% σ(A)=23% , σ(B)=3.87% CV(A)=23%/60%=38.33% CV(B)=3.87%/15%=25.8% 这种情况A项目跟B项目哪个风险高?
你的p怎么看的,A项目总概率都超1了








概念清楚,还有范例,很好!