时间序列平滑模型
出自 MBA智库百科(https://wiki.mbalib.com/)
目录 |
时间序列平滑模型是指运用时间序列平滑法来构建时间序列的一个基础模型。时间序列是指将某一现象所发生的数量变化，依时间的先后顺序排列，以揭示随着时间的推移，这一现象的发展规律，从而用以预测现象发展的方向及其数量。
对于平稳时间序列，可以取最近的n项数值的平均值作为下期的预测值。
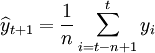
yi为第i期的实际值
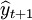为第t+1期的预测值
例 某电子音响器材公司索尼牌单放机的逐月销售量记录如下：
简单移动平均法预测 月份（月） 实际销售（百台） n=3(百台) n=4(百台) 1 20 2 21 3 23 4 24 21.33 5 25 22.67 21.75 6 27 24. 23.33 7 26 25.33 24.75 8 25 26 25.5 9 26 26 25.75 10 28 26.67 26 11 27 26.33 26.25 12 29 27 26.50
N越大，对干扰的敏感性越低，预测的稳定性越好，响应性就越差。对数据不分远近，同等对待。
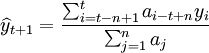
yi为第i期的实际值
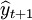为第t+1期的预测值
ai − t + nyi为权重系数
例 当n=3时，a1=0.5， a2=1.0， a3=1.5，
月份（月） 实际销售（百台） 加权移动平均法预测 1 20 2 21 3 23 4 24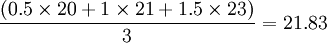 
5 25 23.17 6 27 24.33 7 26 25.83 8 25 26.17 9 26 25.67 10 28 25.67 11 27 26.83 12 29 27.17
n越大，预测的稳定性就好，响应性就越差；n越小，预测的稳定性就越差，响应性就越好。
近期数据的权重越大，则预测的稳定性就越差，响应性就越好；近期数据的权重越小，则预测的稳定性就越好，响应性就越差。
然而，ai和n的选择都没有固定的模式，都带有一定的经验性，究竟选用什么数值，要根据预测的实践而言。
一次指数平滑法的预测公式
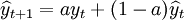
例 某公司的月销售额记录，试取a=0.4和0.7,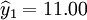
，计算一次指数平滑预测值。
月份（月） 实际销售额yt ayt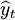 
(1-a)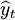
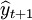
1 10 4 11 6.6 10.6 2 12 3 13 4 16 5 19 6 23 7 26 8 30 9 28 10 18 11 16 12 14
一次指数平滑预测值a=0.7
序号 实际销售额yt ayt 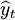(1-a)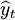
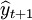
0 10 11 1 12 7 11 3.3 10.3 2 13 8.4 10.3 3.09 11.49 3 16 9.1 11.49 3.45 12.55 4 19 11.2 12.55 3.77 14.97 5 23 13.3 14.97 4.49 17.79 6 26 16.1 17.79 5.34 21.44 7 30 18.2 21.44 6.43 24.63 8 28 21 24.63 7.39 28.39 9 18 19.6 28.39 8.52 28.12 10 16 12.6 28.12 8.44 21.04 11 14 11.2 21.04 6.31 17.51
a选得小一些，预测的稳定性就比较好；反之，响应性比较好。
在有趋势的情况下，一次指数平滑法预测，会出现滞后现象。
指导思想：历史上的销量模式可分解为四组成分：趋势、季节性波动、周期性变化和残差（或随机）波动。
趋势：销售的长期变化，原因包括人口变化、企业营销绩效变化、市场对企业产品和服务的接受程度根本变化。
季节性波动指时间序列中规律性的高峰和低谷，通常每12个月重复一次。造成季节性波动的因素有天气变化、购买模式随日历时间的变化和商品现货供应情况的变化。 周期性变化：需求模式长期的（超过一年）起伏变化。
残差（或随机）波动：总销售量中不能反映趋势、季节性或周期性变化的那一部分构成因素.
